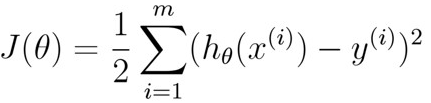对于形如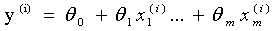 
的线性回归。
假设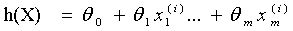
，当
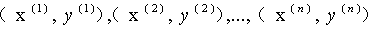的n个数据。注意这里
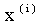表示第i个数据，且他有m个维度。
对于h(X)，这里的目标其实就是估计出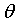
，模型就确定了。这个的计算可以通过最小二乘来估计。
从极大似然的角度来说：
h（X）是假设，但这个模型往往和实际值有差距，通过增加误差来拟合给定数据更加合理。假设误差是独立同分布的，当服从高斯分布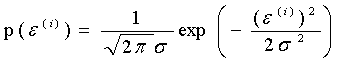
，模型变成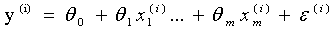
---> 
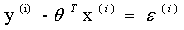
将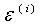
代入高斯分布，再讲其看成是已知数据（x,y）服从的一定关系的高斯分布，运用极大似然估计可以得到
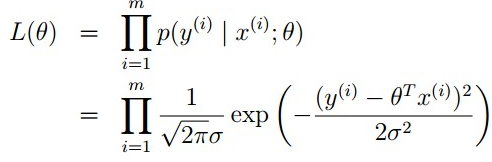
即最小化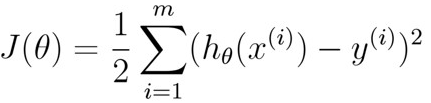
对于形如 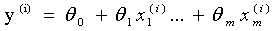的线性回归。
假设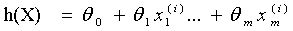，当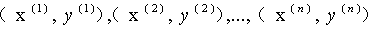的n个数据。注意这里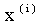表示第i个数据，且他有m个维度。
对于h(X)，这里的目标其实就是估计出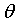，模型就确定了。这个的计算可以通过最小二乘来估计。
从极大似然的角度来说：
h（X）是假设，但这个模型往往和实际值有差距，通过增加误差来拟合给定数据更加合理。假设误差是独立同分布的，当服从高斯分布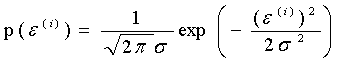
，模型变成 --->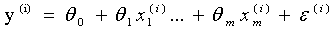
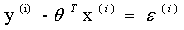
将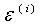代入高斯分布，再讲其看成是已知数据（x,y）服从的一定关系的高斯分布，运用极大似然估计可以得到
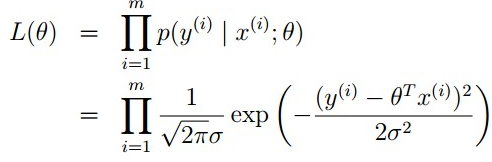
即最小化