[ZJOI2012]网络

题目描述

有一个无向图G，每个点有个权值，每条边有一个颜色。这个无向图满足以下两个条件：

1. 对于任意节点连出去的边中，相同颜色的边不超过两条。

2. 图中不存在同色的环，同色的环指相同颜色的边构成的环。

在这个图上，你要支持以下三种操作：

0. 修改一个节点的权值。

1. 修改一条边的颜色。

2. 查询由颜色c的边构成的图中，所有可能在节点u到节点v之间的简单路径上的节点的权值的最大值。

输入输出格式

输入格式：

输入文件network.in的第一行包含四个正整数N, M, C, K，其中N为节点个数，M为边数，C为边的颜色数，K为操作数。

接下来N行，每行一个正整数vi，为节点i的权值。

之后M行，每行三个正整数u, v, w，为一条连接节点u和节点v的边，颜色为w。满足1 ≤ u, v ≤ N，0 ≤ w < C，保证u ≠ v，且任意两个节点之间最多存在一条边(无论颜色)。

最后K行，每行表示一个操作。每行的第一个整数k表示操作类型。

0. k = 0为修改节点权值操作，之后两个正整数x和y，表示将节点x的权值vx修改为y。

1. k = 1为修改边的颜色操作，之后三个正整数u, v和w，表示将连接节点u和节点v的边的颜色修改为颜色w。满足0 ≤ w < C。

2. k = 2为查询操作，之后三个正整数c, u和v，表示查询所有可能在节点u到节点v之间的由颜色c构成的简单路径上的节点的权值的最大值。如果不存在u和v之间不存在由颜色c构成的路径，那么输出“-1”。

输出格式：

输出文件network.out包含若干行，每行输出一个对应的信息。

1. 对于修改节点权值操作，不需要输出信息。

2. 对于修改边的颜色操作，按以下几类输出：

a) 若不存在连接节点u和节点v的边，输出“No such edge.”。

b) 若修改后不满足条件1，不修改边的颜色，并输出“Error 1.”。

c) 若修改后不满足条件2，不修改边的颜色，并输出“Error 2.”。

d) 其他情况，成功修改边的颜色，并输出“Success.”。

输出满足条件的第一条信息即可，即若同时满足b和c，则只需要输出“Error 1.”。

3. 对于查询操作，直接输出一个整数。

输入输出样例

输入样例#1：

4 5 2 7
1
2
3
4
1 2 0
1 3 1
2 3 0
2 4 1
3 4 0
2 0 1 4
1 1 2 1
1 4 3 1
2 0 1 4
1 2 3 1
0 2 5
2 1 1 4

输出样例#1：

4
Success.
Error 2.
-1
Error 1.
5

说明

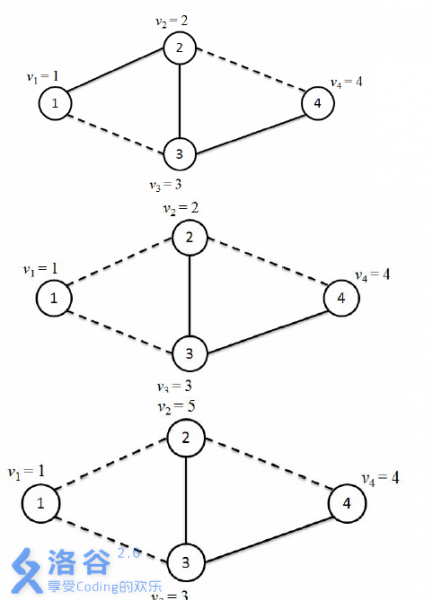
颜色0为实线的边，颜色1为虚线的边，

由颜色0构成的从节点1到节点4的路径有1 – 2 – 4，故max{v1, v2, v4} = max{ 1, 2, 4 } = 4。

将连接节点1和节点2的边修改为颜色1，修改成功，输出“Success.”

将连接节点4和节点3的边修改为颜色1，由于修改后会使得存在由颜色1构成的环( 1 – 2 – 4 – 3 – 1 )，不满足条件2，故不修改，并输出“Error 2”。

不存在颜色0构成的从节点1到节点4的边，输出“-1”。

将连接节点2和节点3的边修改为颜色1，由于修改后节点2的连出去的颜色为1的边有3条，故不满足条件1，故不修改，并输出“Error 1.”。

将节点2的权值修改为5。

由颜色1构成的从节点1到节点4的路径有 1 – 2 – 4，故max{v1, v2, v4} = max{ 1, 5, 4 } = 5。

【数据规模】

对于30%的数据：N ≤ 1000，M ≤ 10000，C ≤ 10，K ≤ 1000。

另有20%的数据：N ≤ 10000，M ≤ 100000，C = 1，K ≤ 100000。

对于100%的数据：N ≤ 10000，M ≤ 100000，C ≤ 10，K ≤ 100000。

 

 

考虑C<=10,那么就维护C个LCT.

对于0操作,直接把每个LCT里面的权值修改.

对于1操作,可以先用map记录下每条边的颜色(其实最好是不用map,只是比较方便,卡着时间过了就没管了).然后就先进行一大堆判断,然后把原来那条边删掉,新加一条边.对于Error1的处理,每个点维护一个cnt,表示这个点的度数,因为在旋转的操作中这个值不会变,那么就link的时候+1,cut的时候-1.

对于2操作,每个点维护一个zd表示以这个点为根的splay子树(不是原树)里面的最大值,查询的时候先把x变成root,然后access
y,splay y.答案就是zd[y].

在cut和Rotate时都要更新这个zd值.

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<algorithm>
#include<map>
#include<complex>
#include<queue>
#include<stack>
#include<cmath>
#include<set>
#include<vector>
#define maxn 20010
#define pre t[x].fa
#define ls t[x].ch[0]
#define rs t[x].ch[1]
#define RG register
using namespace std;
struct LCT{
  struct data{int w,ch[2],fa,lazy,cnt,zd;}t[maxn];
  inline bool son(RG int x){return t[pre].ch[1]==x;}
  inline bool isrt(RG int x){return t[pre].ch[0]!=x && t[pre].ch[1]!=x;}
  inline void updata(int x){t[x].zd=max(t[x].w,max(t[ls].zd,t[rs].zd));}
  inline void down(RG int x){
    if(t[x].lazy==1)
      swap(ls,rs),t[ls].lazy^=1,t[rs].lazy^=1,t[x].lazy=0;
  }
  void pd(int x){if(!isrt(x)) pd(pre);down(x);}
  inline void Rotate(RG int x){
    int f=t[x].fa,g=t[f].fa,c=son(x);
    if(!isrt(f)) t[g].ch[son(f)]=x;
    t[x].fa=g;
    t[f].ch[c]=t[x].ch[c^1],t[t[f].ch[c]].fa=f;
    t[x].ch[c^1]=f,t[f].fa=x;
    updata(f),updata(x);
  }
  inline void Splay(RG int x){
    pd(x);
    for(;!isrt(x);Rotate(x)){
      if(!isrt(pre)) Rotate(son(pre)==son(x)?pre:x);
    }
  }
  inline void access(RG int x){
    for(RG int y=0;x;y=x,x=pre) Splay(x),rs=y,updata(x);
  }
  inline void makert(RG int x){
    access(x),Splay(x),t[x].lazy^=1;
  }
  inline int findrt(RG int x){
    access(x),Splay(x);
    while(ls) down(x),x=ls;
    return x;
  }
  inline void link(RG int x,RG int y){
    makert(x),t[x].fa=y;t[x].cnt++,t[y].cnt++;
  }
  inline void cut(RG int x,RG int y){
    makert(x),access(y),Splay(y);
    t[y].ch[0]=t[x].fa=0;
    t[x].cnt--,t[y].cnt--;
    updata(y);
  }
  inline void query(int x,int y){
    if(findrt(x)!=findrt(y)) printf("-1
");
    else{
      makert(x),access(y),Splay(y);
      printf("%d
",t[y].zd);
    }
  }
}lct[12];
struct edge{
  int x,y;
  bool operator < (const edge &h) const{
    if(h.x!=x)return h.x<x;else return h.y<y;
  }
};
map<edge,int>mp;
int main(){
  int n,m,C,qes,x,y,z,type;
  scanf("%d%d%d%d",&n,&m,&C,&qes);
  for(RG int i=1;i<=n;i++){
    scanf("%d",&x);
    for(RG int j=0;j<C;j++)lct[j].t[i].w=x;
  }
  for(RG int i=1;i<=m;i++){
    scanf("%d%d%d",&x,&y,&z),lct[z].link(x,y);
    edge e1=(edge){x,y},e2=(edge){y,x};
    mp[e1]=mp[e2]=z;
  }
  for(RG int i=1;i<=qes;i++){
    scanf("%d",&type);
    if(type==0){
      scanf("%d%d",&x,&y);
      for(int j=0;j<C;j++) lct[j].t[x].w=y,lct[j].Splay(x);
    }
    if(type==1){
      scanf("%d%d%d",&x,&y,&z);
      edge e1=(edge){x,y},e2=(edge){y,x};
      if(!mp.count((e1))){printf("No such edge.
");continue;}
      int las=mp[e1];
      if(las==z){printf("Success.
");continue;}
      if(lct[z].t[x].cnt>=2 || lct[z].t[y].cnt>=2){printf("Error 1.
");continue;}
      if(lct[z].findrt(x)==lct[z].findrt(y)){printf("Error 2.
");continue;}
      lct[las].cut(x,y);
      mp[e1]=mp[e2]=z;
      lct[z].link(x,y);
      printf("Success.
");
    }
    if(type==2) scanf("%d%d%d",&z,&x,&y),lct[z].query(x,y);
  }
  return 0;
}