数据结构与Python实现
分类和时空复杂度
分类:
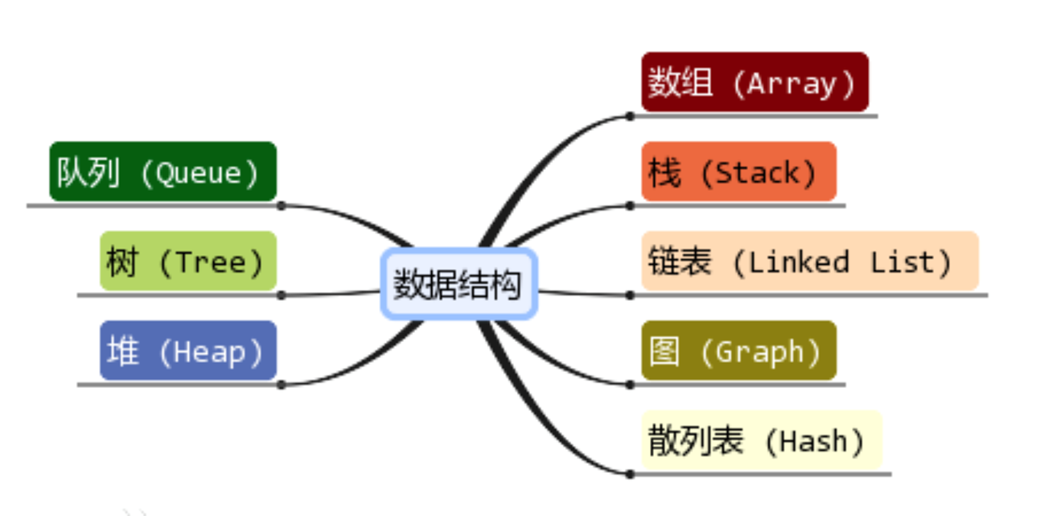
时间和空间复杂度:
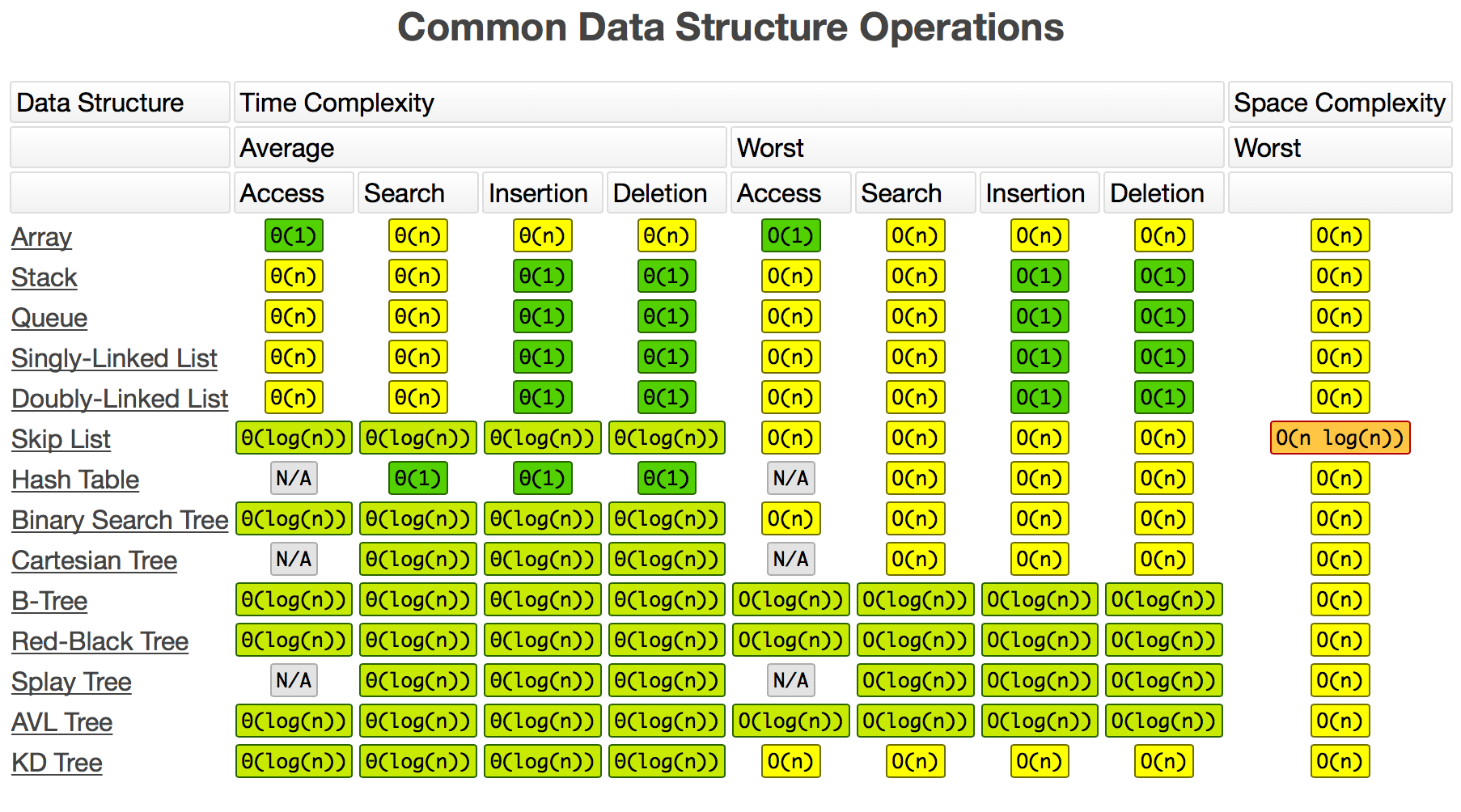
Array
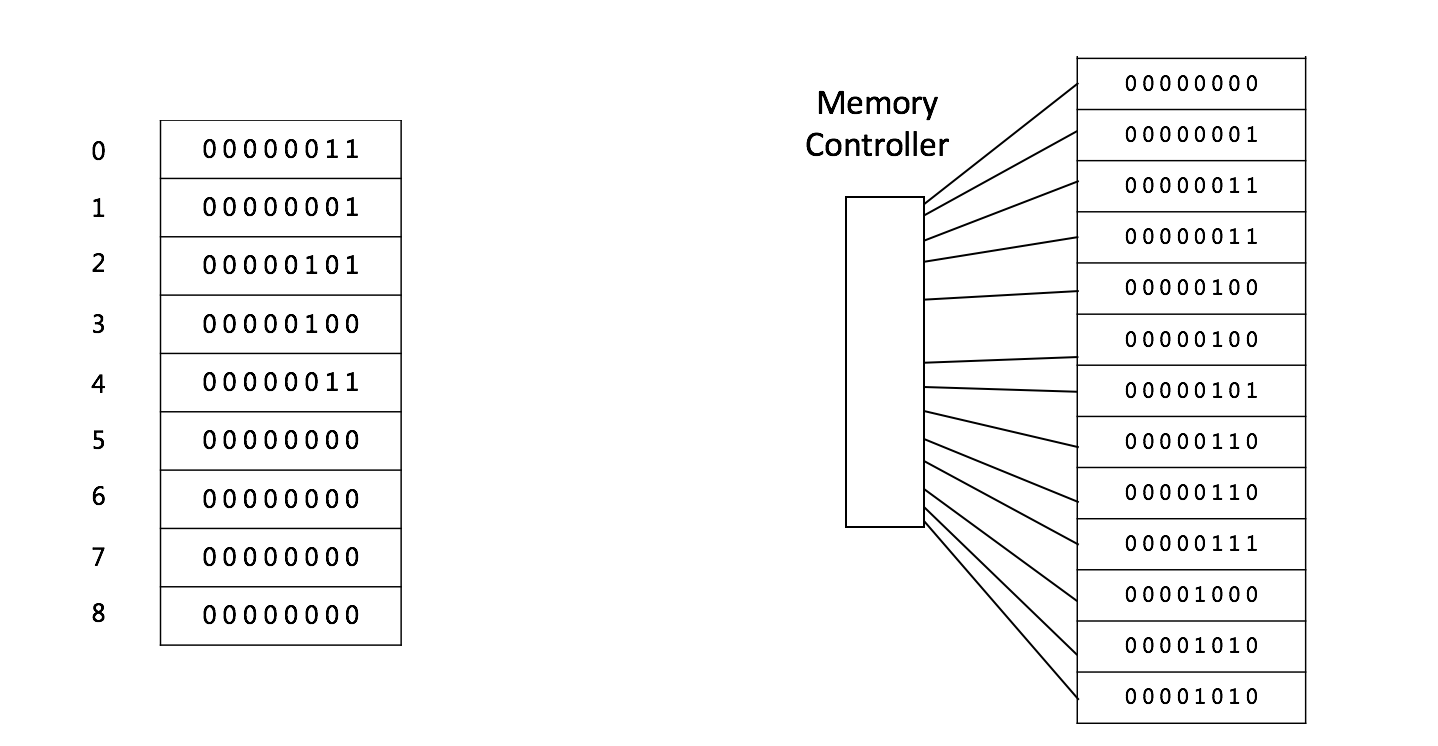
数组是可以再内存中连续存储多个元素的结构,在内存中的分配也是连续的,数组中的元素通过数组下标进行访问,数组下标从0开始。
适用场景:
- 频繁查询,对存储空间要求不大,很少增加和删除的情况
优点:
- 按照索引查询元素速度快
- 按照索引遍历数组方便
缺点:
- 数组的大小固定后就无法扩容了
- 数组只能存储一种类型的数据
- 添加,删除的操作慢,因为要移动其他的元素
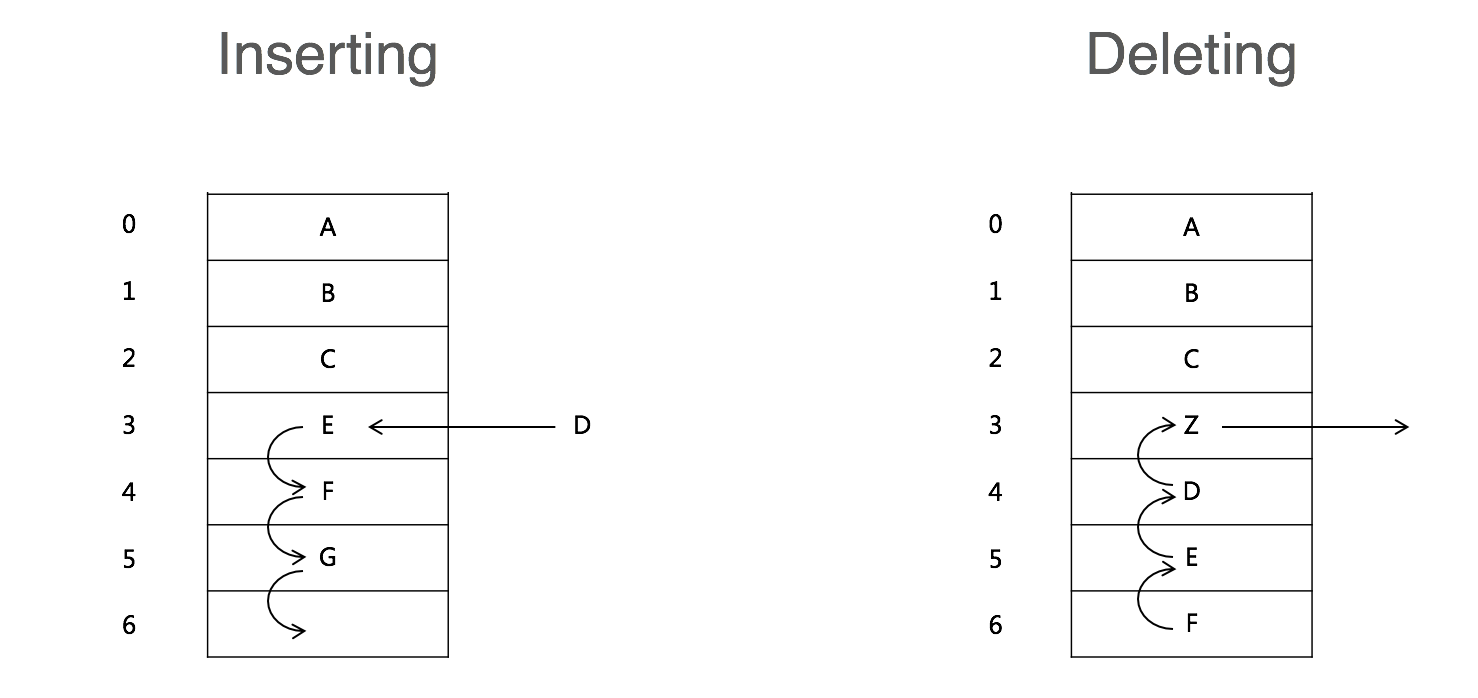
| 时间复杂度 | O() |
|---|---|
| Access | O(1) |
| Insert | O(n) |
| Delete | O(n) |
Linked List
Linked List
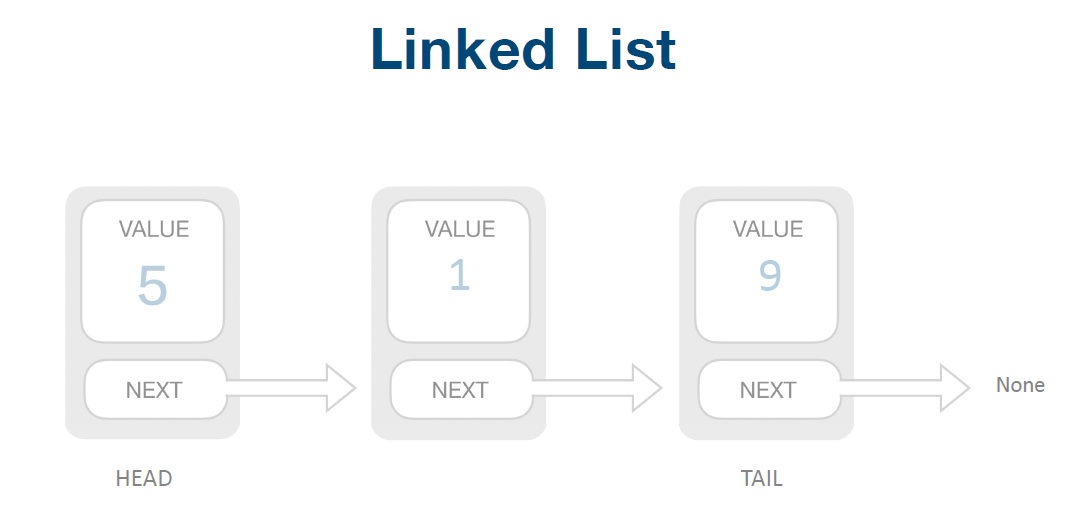
链表是物理存储单元上非连续的、非顺序的存储结构;
数据元素的逻辑顺序是通过链表的指针地址实现,每个元素(结点)包含两个域,一个是存储元素的数据域 (内存空间),另一个是指向下一个结点地址的指针域。
根据指针的指向,链表能形成不同的结构,例如单链表,双向链表,循环链表等。
链表插入Node:
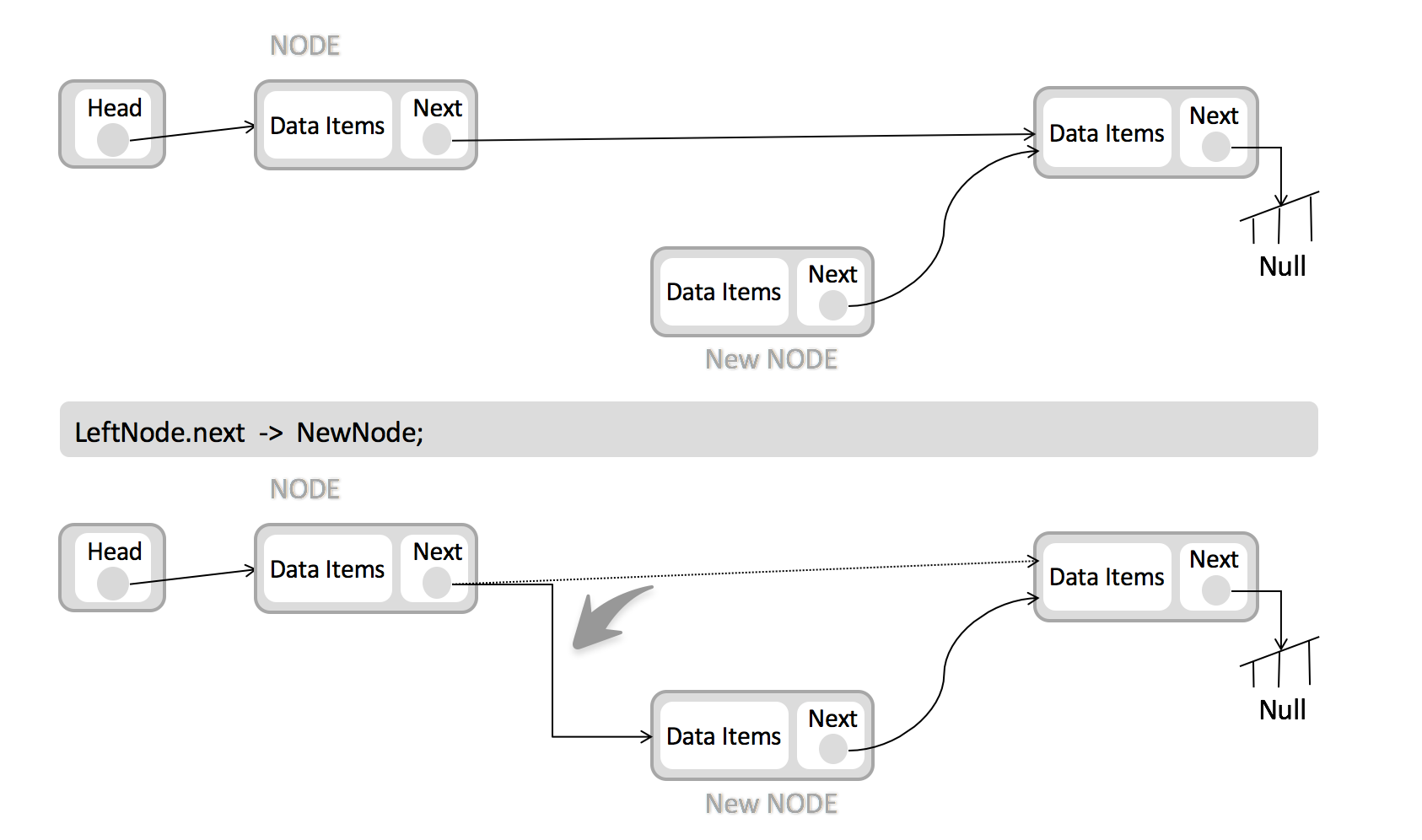
链表删除Node:
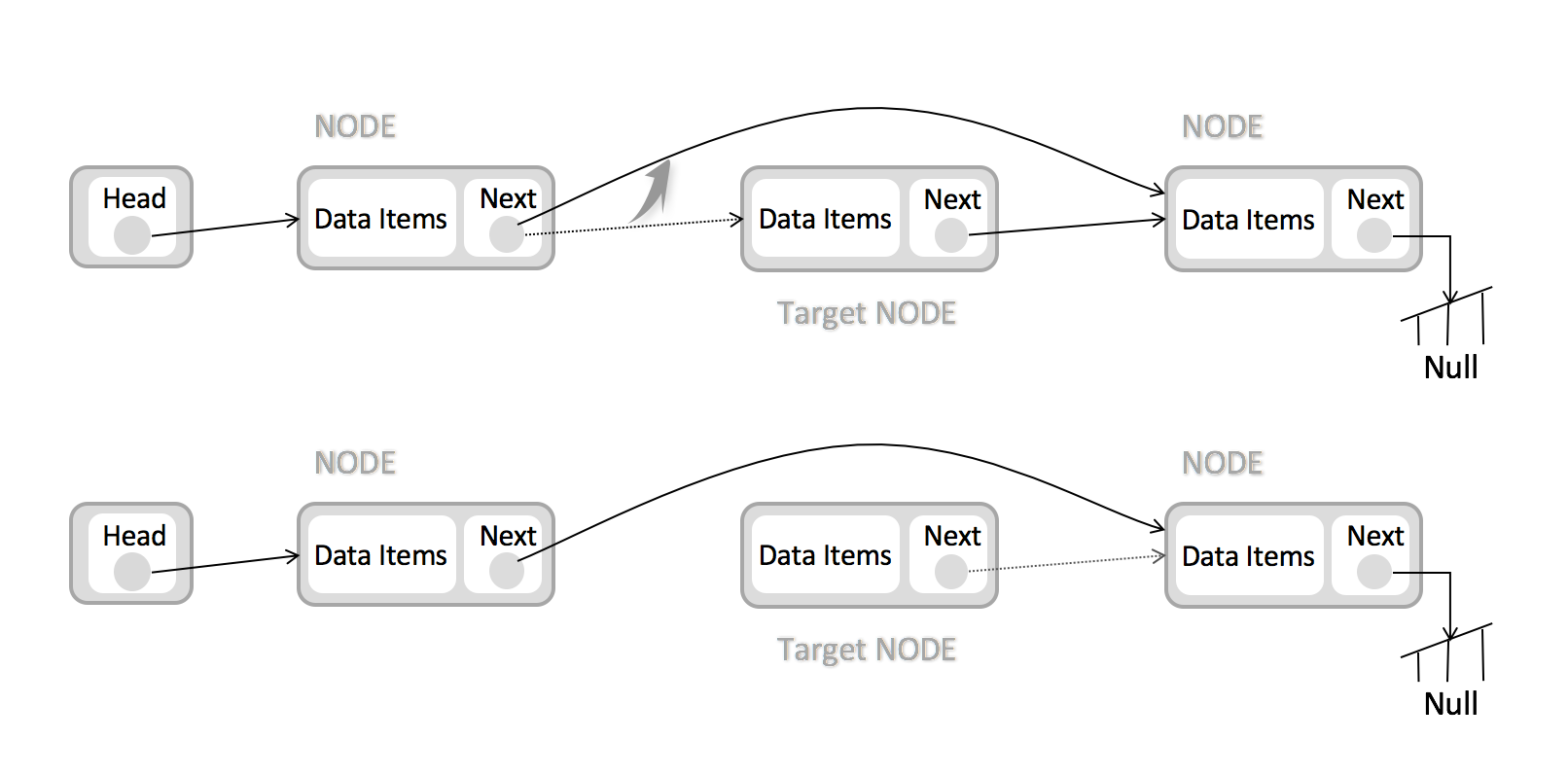
| 时间复杂度 | O() |
|---|---|
| space | O(1) |
| prepend | O(1) |
| append | O(1) |
| lookup | O(n) |
| insert | O(1) |
| delete | O(1) |
Double Linked List
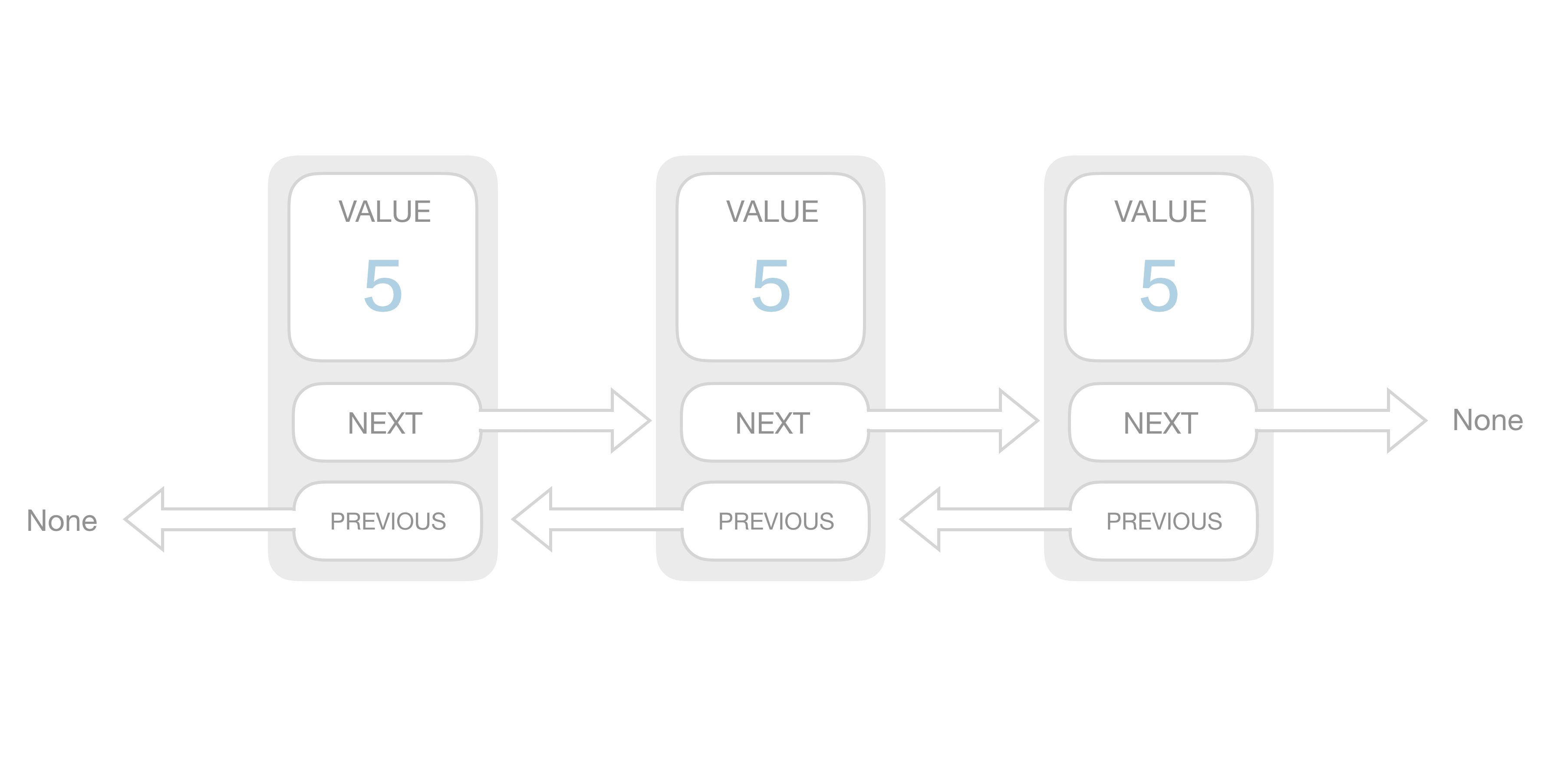
Circular Linked List

Stack
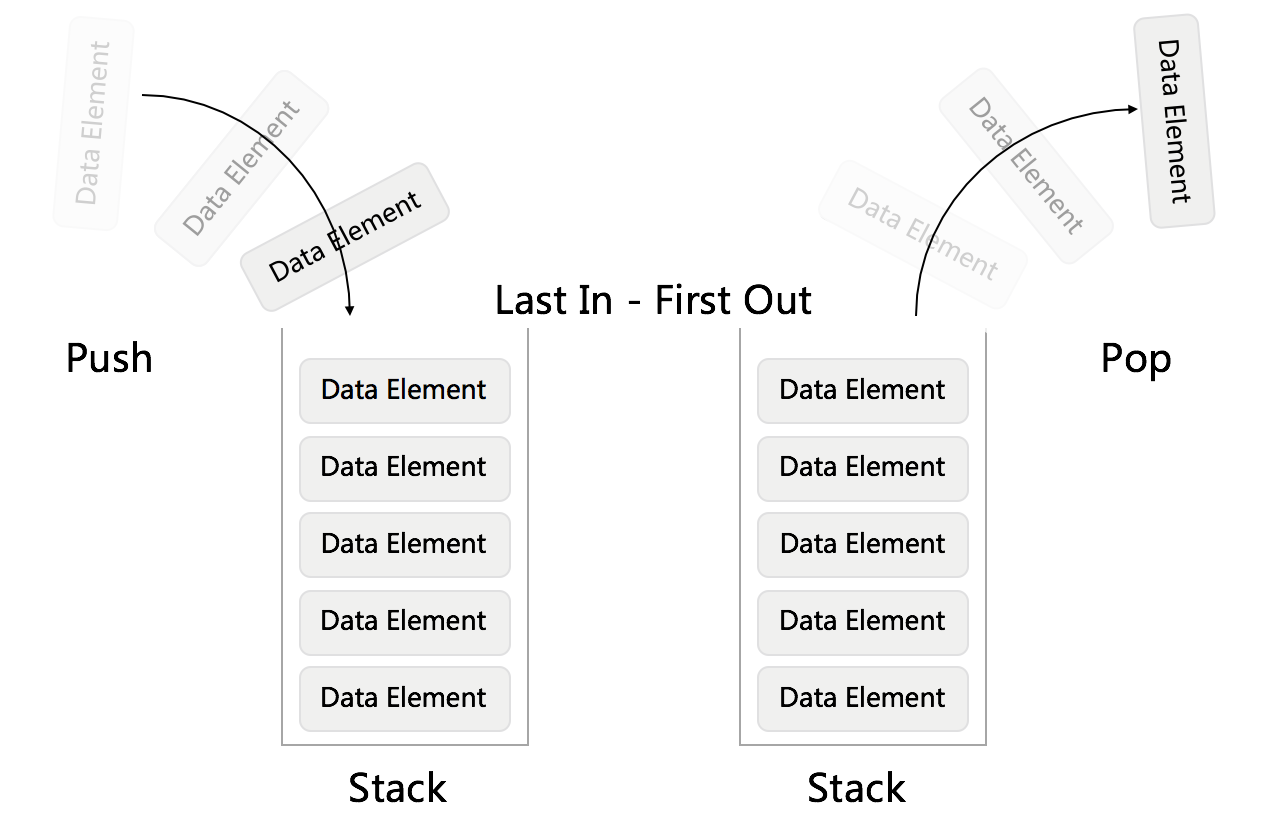
栈是一种特殊的线性表;仅能在线性表的一端操作,栈顶允许操作,栈底不允许操作。
栈的特点:
- 后进先出,从栈顶放入元素的操作叫入栈,取出元素叫出栈。
Queue
Queue

队列与栈一样,也是一种线性表;队列可以在一端添加元素,在另一端取出元素,也就是“先进先出”;从一端放入元素的操作称为入队,取出元素为出队 ;
使用情景:
- 在多线程阻塞队列管理中非常适用
Double-ended Queue
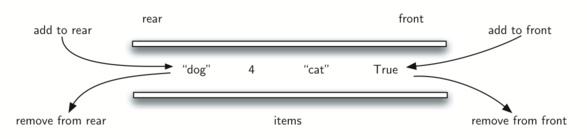
双端队列和普通队列区别在于:队头和队尾都可以插入和删除元素;
Priority Queue
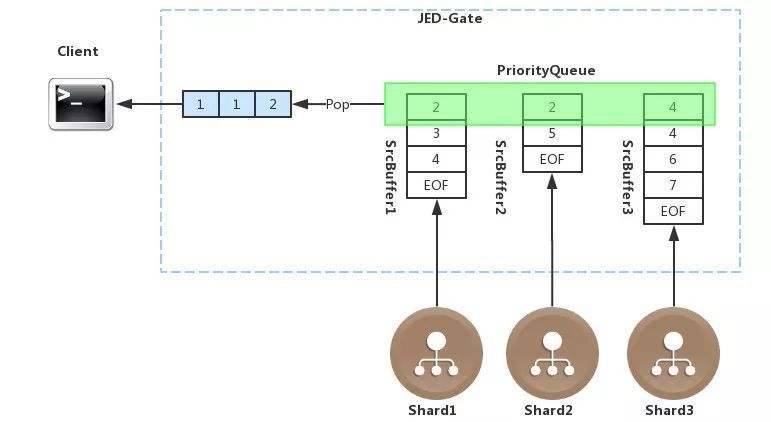
优先队列:正常⼊、按照优先级出
Tree
Tree
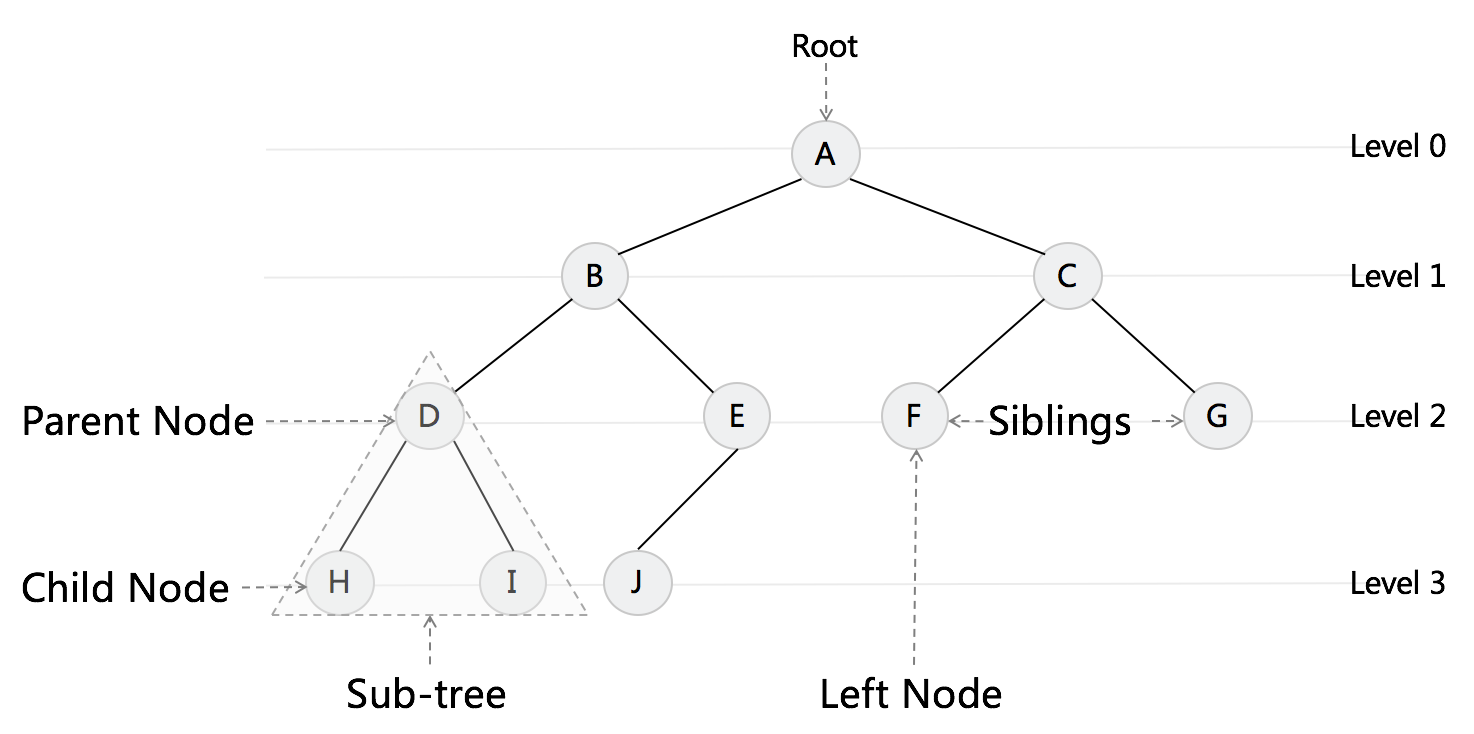
树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做 “树” 是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
树的特点:
- 每个节点有零个或多个子节点
- 没有父节点的节点称为根节点
- 每一个非根节点有且只有一个父节点
- 除了根节点外,每个子节点可以分为多个不相交的子树
Binary Tree
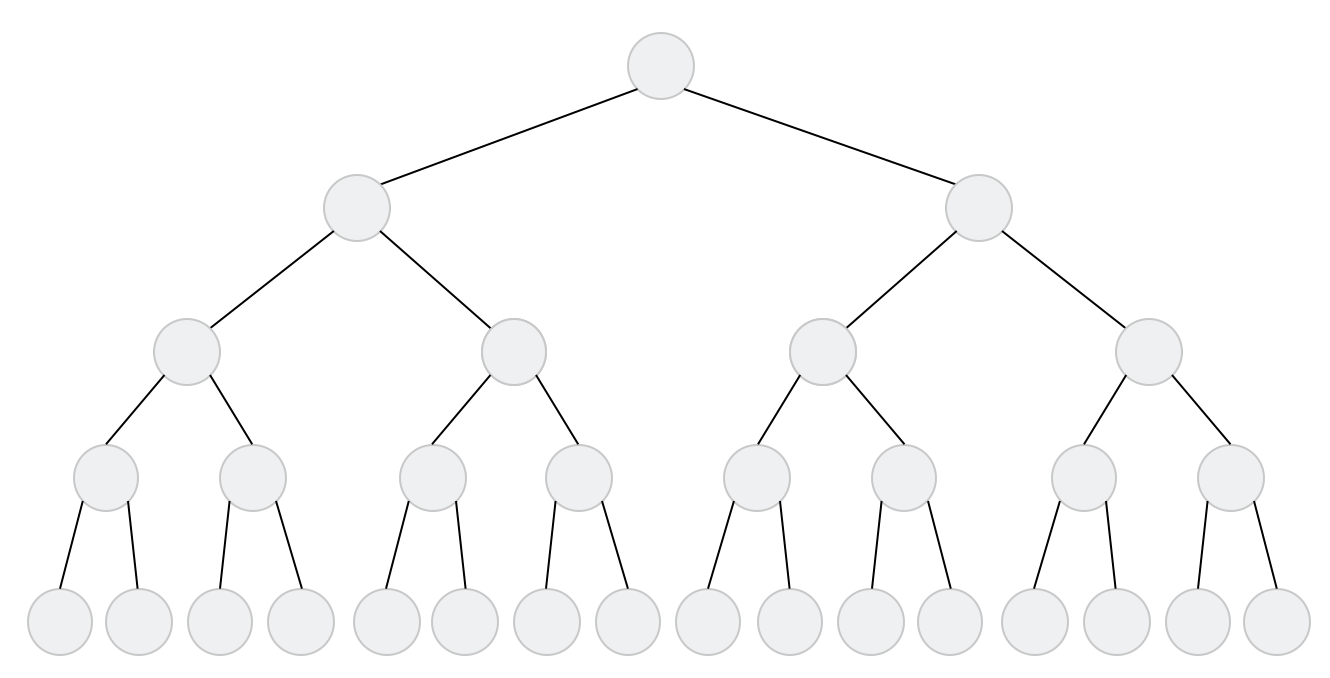
二叉树:
- 每个结点最多有两颗子树,结点的度最大为2
- 左子树和右子树是有顺序的,次序不能颠倒
- 即使某结点只有一个子树,也要区分左右子树
Binary Search Tree
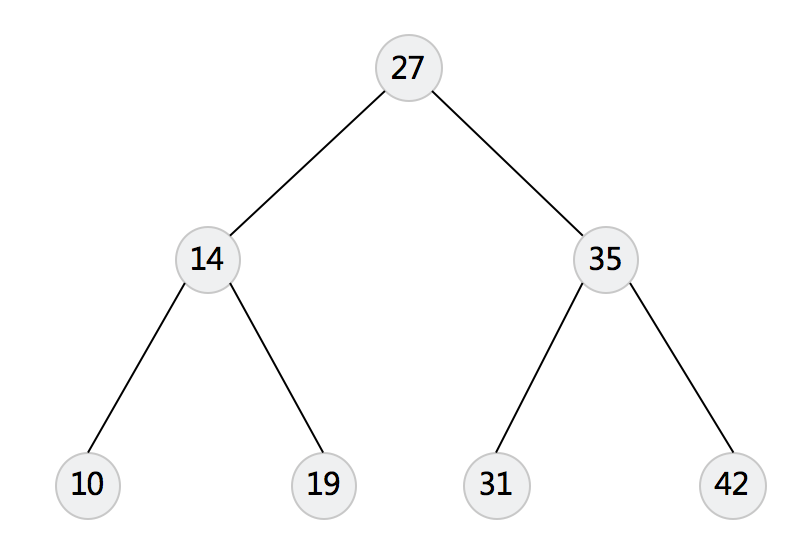
二叉搜索树:
- 若任意节点的左⼦子树不为空,则左子树上所有结点的值均小于它的根结点的值;
- 若任意节点的右⼦子树不为空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉搜索树
Heap
堆是一种比较特殊的数据结构,可以被看做一棵树的数组对象,具有以下的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树
Mini Heap
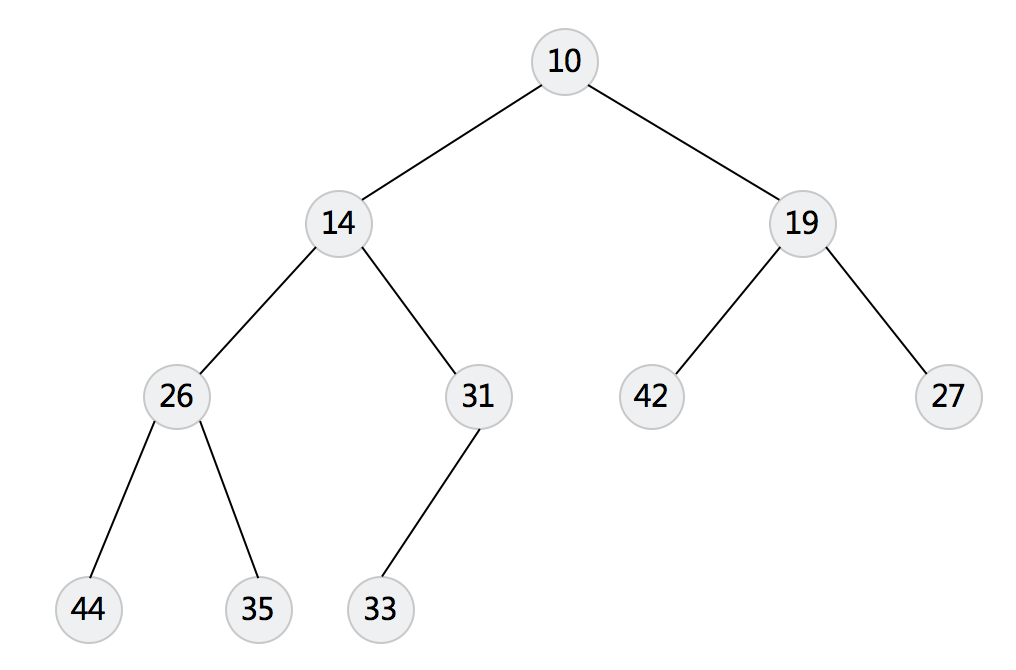
小顶堆特点:
- 任意节点的值小于父节点的值
- 完整的二叉树
Max Heap
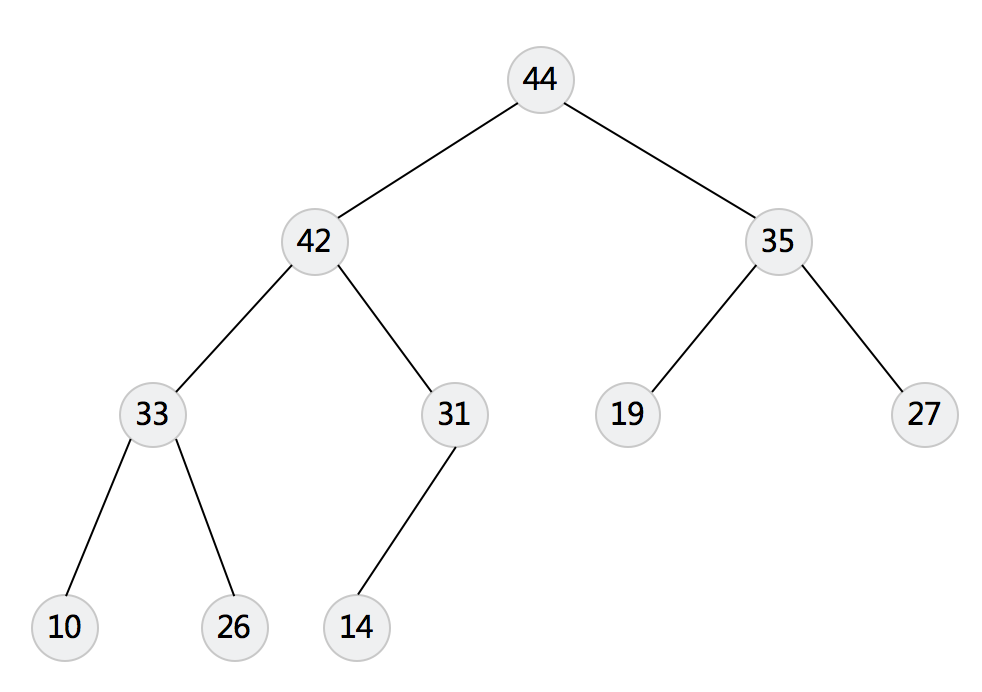
大顶堆特点:
- 任意节点的值大于父节点的值
- 完全的二叉树
Graph
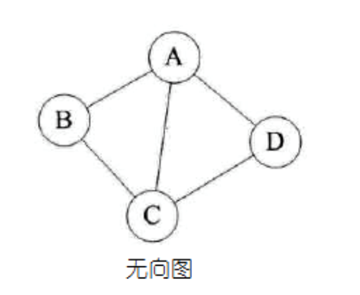
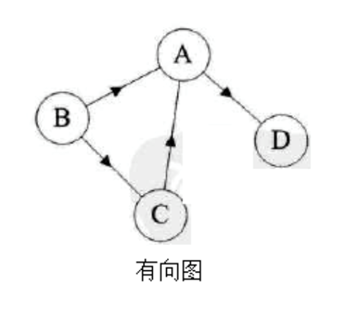
图是由结点的有穷集合V和边的集合E组成。其中,为了与树形结构加以区别,在图结构中常常将结点称为顶点,边是顶点的有序偶对;若两个顶点之间存在一条边,就表示这两个顶点具有相邻关系。
Hash Table
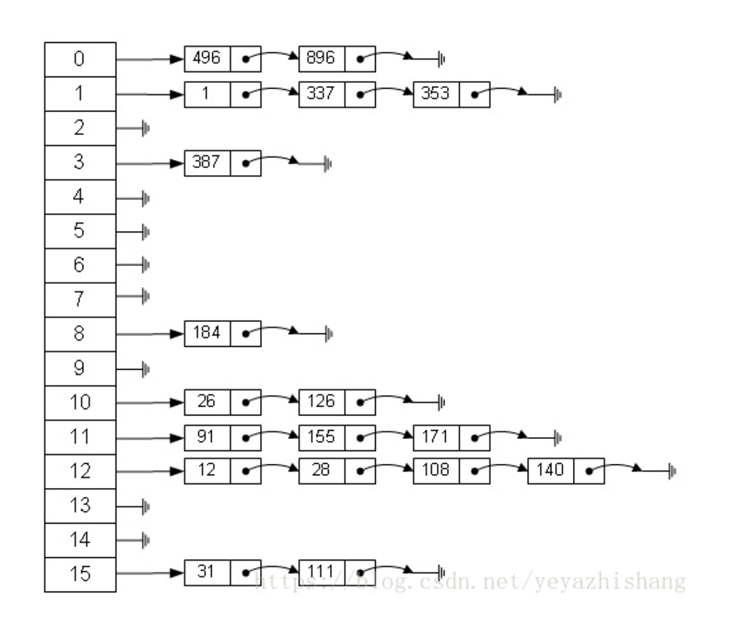
哈希表,是根据关键码和值 (key和value) 直接进行访问的数据结构,哈希底层算法是取模(取余)运算,所以会产生哈希冲突。
哈希冲突解决:拉链法