
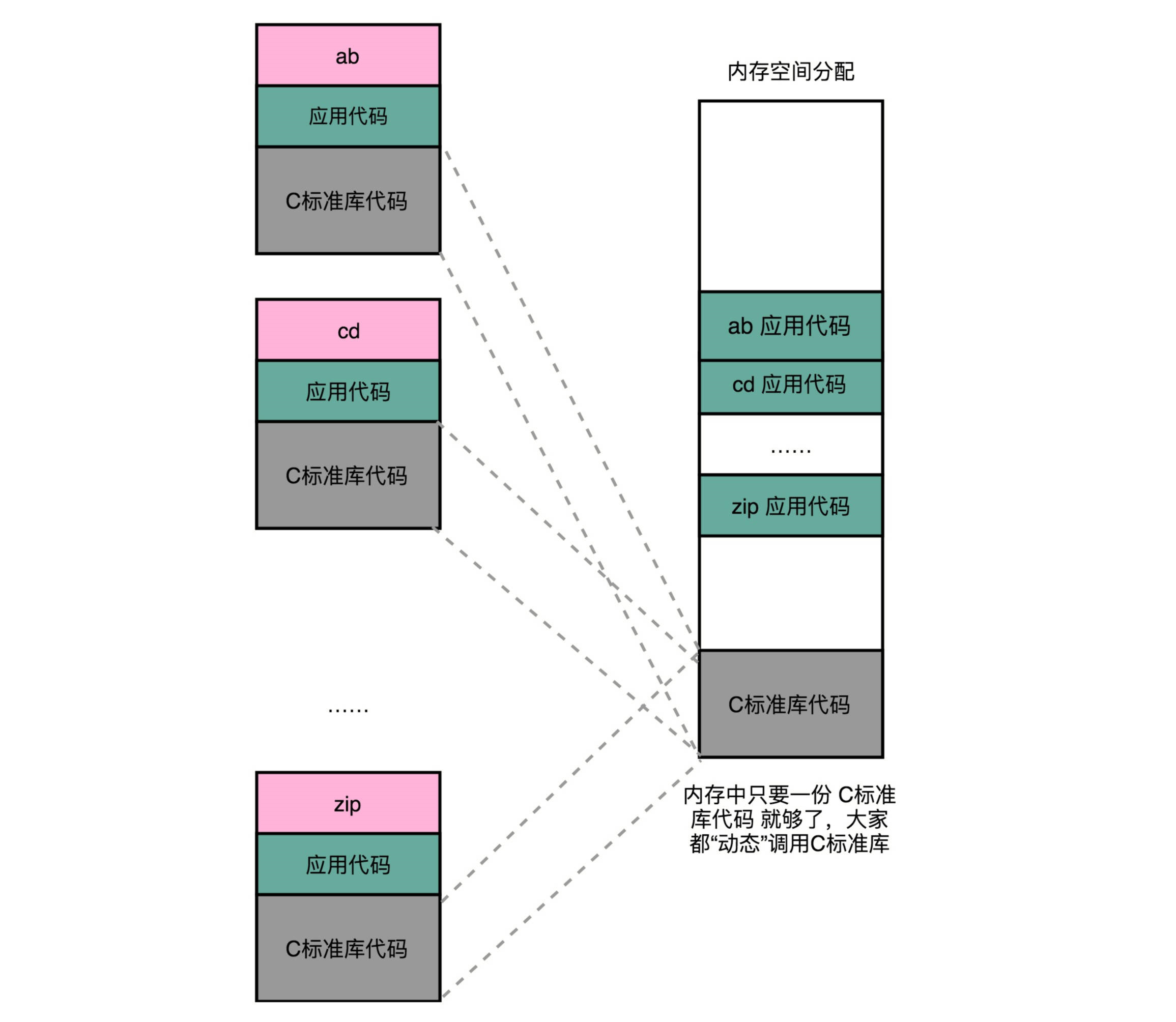
1、动态链接是什么
程序的链接,是把对应的不同文件内的代码段,合并到一起,成为最后的可执行文件。这个链接的方式,让我们在写代码的时候做到了“复用”。同样的功能代码只要写一次,然后提供给很多不同的程序进行链接就行了。如果有很多个程序都要通过装载器装载到内存里面,那里面链接好的同样的功能代码,也都需要再装载一遍,再占一遍内存空间。解决程序装载到内存的时候,最根本的问题其实就是内存空间不够用。最合理们的一个解决方案是,能够让同样功能的代码,在不同的程序里面,不需要各占一份内存空间,这个思路就引入一种新的链接方法,叫作动态链接(Dynamic Link)。相应的,我们之前说的合并代码段的方法,就是静态链接(Static Link)。
这个加载到内存中的共享库会被很多个程序的指令调用到。在 Windows 下,这些共享库文件就是.dll 文件,也就是 Dynamic-Link Libary(DLL,动态链接库)。在 Linux 下,这些共享库文件就是.so 文件,也就是 Shared Object(一般我们也称之为动态链接库)。这两大操作系统下的文件名后缀,一个用了“动态链接”的意思,另一个用了“共享”的意思,正好覆盖了两方面的含义。
2、二进制
程序 = 算法 + 数据结构。如果对应到组成原理或者说硬件层面,算法就是各种计算机指令,数据结构就对应二进制数据。现代计算机都是用 0 和 1 组成的二进制,来表示所有的信息。存储在内存里面的字符串、整数、浮点数也都是用二进制表示的。万事万物在计算机里都是 0 和 1。
二进制和平时用的十进制,其实并没有什么本质区别,只是平时我们是“逢十进一”,这里变成了“逢二进一”而已。每一位,相比于十进制下的 0~9 这十个数字,只能用 0 和 1 这两个数字。
3、字符串标识
不仅数值可以用二进制表示,字符乃至更多的信息都能用二进制表示。最典型的例子就是字符串(Character String)。最早计算机只需要使用英文字符,加上数字和一些特殊符号,然后用 8 位的二进制,就能表示我们日常需要的所有字符了,这个就是我们常常说的 ASCII 码(American Standard Code for Information Interchange,美国信息交换标准代码)。
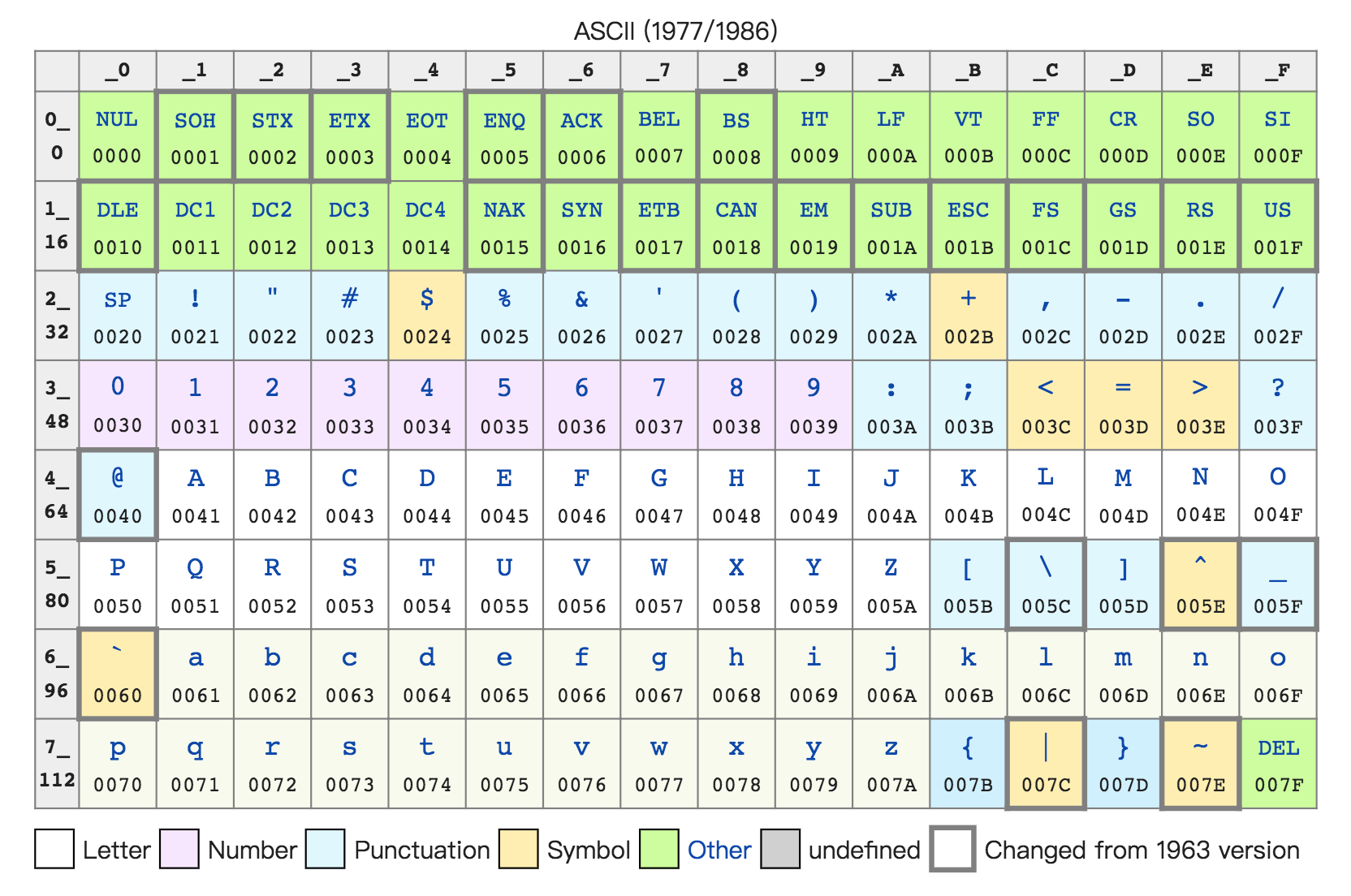
ASCII 码就好比一个字典,用 8 位二进制中的 128 个不同的数,映射到 128 个不同的字符里。比如,小写字母 a 在 ASCII 里面,就是第 97 个,也就是二进制的 0110 0001,对应的十六进制表示就是 61。而大写字母 A,就是第 65 个,也就是二进制的 0100 0001,对应的十六进制表示就是 41。
在 ASCII 码里面,数字 9 不再像整数表示法里一样,用 0000 1001 来表示,而是用 0011 1001 来表示。字符串 15 也不是用 0000 1111 这 8 位来表示,而是变成两个字符 1 和 5 连续放在一起,也就是 0011 0001 和 0011 0101,需要用两个 8 位来表示。
们可以看到,最大的 32 位整数,就是 2147483647。如果用整数表示法,只需要 32 位就能表示了。但是如果用字符串来表示,一共有 10 个字符,每个字符用 8 位的话,需要整整 80 位。比起整数表示法,要多占很多空间。
这也是为什么,很多时候我们在存储数据的时候,要采用二进制序列化这样的方式,而不是简单地把数据通过 CSV 或者 JSON,这样的文本格式存储来进行序列化。不管是整数也好,浮点数也好,采用二进制序列化会比存储文本省下不少空间。
4、计算机为什么选择二进制
(1)易于物理实现
因为具有两种稳定状态的物理原件是很多的,如门电路的导通与截止,电压的高与底,而他们恰好对应表示1和0两个字符。假如采用十进制,要制造具有10种稳定状态的物理电路,那是非常困难的。
(2)二进制数运算简单
数学推导证明,对R进制算术的求和、求积规则各有R(R+1)/2中。如采用十进制就有55种求和与求积的运算规则;而二进制仅各有三种,因而简化了运算器等物理器件的设计。
(3)机器可靠性高
由于电压的高低,电流的有无等都是一种质的变化,两种状态分明。所以基2码的传递抗干扰能力强,鉴别信息的可靠性高。
(4)通用性强
基2码不仅成功地运用于数值信息编码(二进制),而且适用于各种非数值信息的数字化编码。特别是仅有的两个符号0和1恰好与逻辑命题的两个值“真”和“假”相对应,从而为计算机实现逻辑运算和逻辑判断提供了方便。
5、电信号传输的概念
从信息编码的角度来说,金、鼓、灯塔、烽火台类似电报的二进制编码。电报传输的信号有两种,一种是短促的点信号(dot 信号),一种是长一点的划信号(dash 信号)。我们把“点”当成“1”,把“划”当成“0”。这样一来,我们的电报信号就是另一种特殊的二进制编码了。电影里最常见的电报信号是“SOS”,这个信号表示出来就是 “点点点划划划点点点”。
比起灯塔和烽火台这样的设备,电报信号有两个明显的优势。第一,信号的传输距离迅速增加。因为电报本质上是通过电信号来进行传播的,所以从输入信号到输出信号基本上没有延时。第二,输入信号的速度加快了很多。电报机只有一个按钮,按下就是输入信号,按的时间短一点,就是发出了一个“点”信号;按的时间长一些,就是一个“划”信号。只要一个手指,就能快速发送电报。而且,制造一台电报机也非常容易。电报机本质上就是一个“蜂鸣器 + 长长的电线 + 按钮开关”。蜂鸣器装在接收方手里,开关留在发送方手里。双方用长长的电线连在一起。当按钮开关按下的时候,电线的电路接通了,蜂鸣器就会响。短促地按下,就是一个短促的点信号;按的时间稍微长一些,就是一个稍长的划信号。
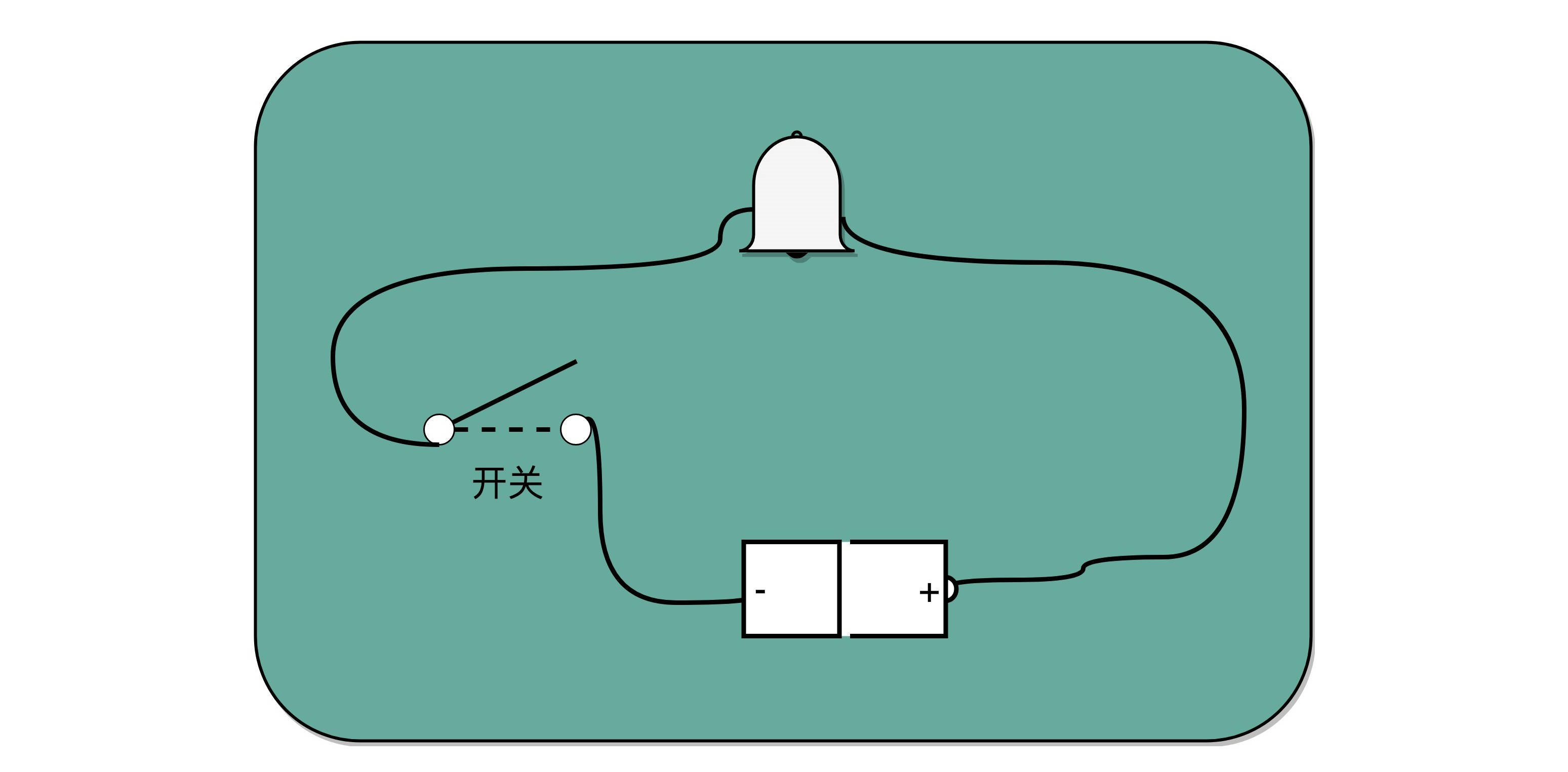
有了电报机,只要铺设好电报线路,就可以传输我们需要的讯息了。但是这里面又出现了一个新的挑战,就是随着电线的线路越长,电线的电阻就越大。当电阻很大,而电压不够的时候,即使你按下开关,蜂鸣器也不会响。
对于电报来说,电线太长了,使得线路接通也没有办法让蜂鸣器响起来。那么,我们就不要一次铺太长的线路,而把一小段距离当成一个线路,也和驿站建立一个小电报站。我们在小电报站里面安排一个电报员,他听到上一个小电报站发来的信息,然后原样输入,发到下一个电报站去。这样,我们的信号就可以一段段传输下去,而不会因为距离太长,导致电阻太大,没有办法成功传输信号。为了能够实现这样接力传输信号,在电路里面,工程师们造了一个叫作继电器(Relay)的设备。
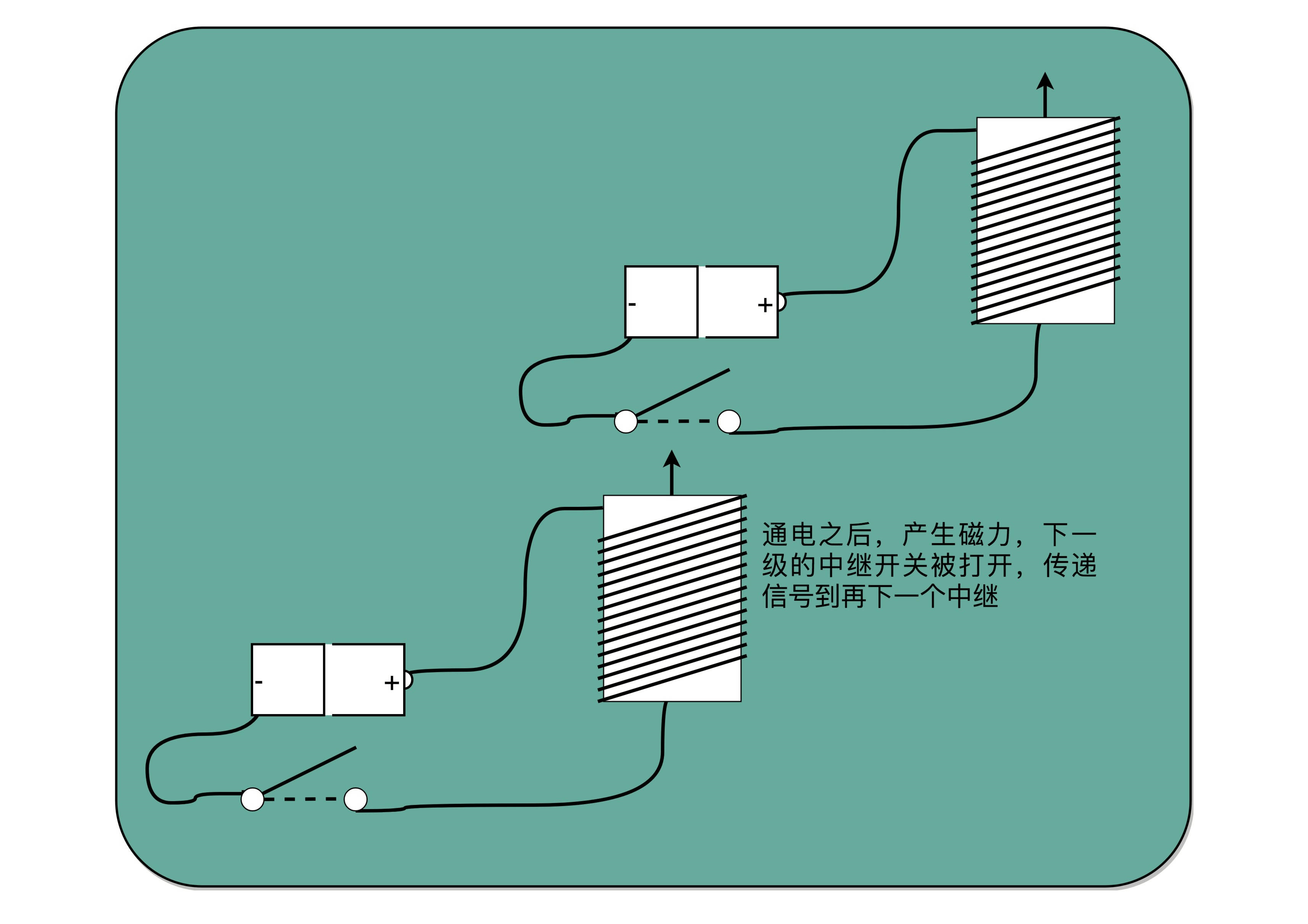
这个过程中,需要在每一阶段原样传输信号,事实上可以使用一种设备代替这种传递工作。把原先用来输出声音的蜂鸣器,换成一段环形的螺旋线圈,让电路封闭通上电。因为电磁效应,这段螺旋线圈会产生一个带有磁性的电磁场。原本需要输入的按钮开关,就可以用一块磁力稍弱的磁铁把它设在“关”的状态。这样,按下上一个电报站的开关,螺旋线圈通电产生了磁场之后,磁力就会把开关“吸”下来,接通到下一个电报站的电路。在中间所有小电报站都用这个“螺旋线圈 + 磁性开关”的方式,来替代蜂鸣器和普通开关,而只在电报的始发和终点用普通的开关和蜂鸣器,就有了一个拆成一段一段的电报线路,接力传输电报信号。事实上,继电器还有一个名字就叫作电驿,这个“驿”就是驿站的驿。
有了继电器之后,我们不仅有了一个能够接力传输信号的方式,更重要的是,和输入端通过开关的“开”和“关”来表示“1”和“0”一样,我们在输出端也能表示“1”和“0”了。
输出端的作用,不仅仅是通过一个蜂鸣器或者灯泡,提供一个供人观察的输出信号,通过“螺旋线圈 + 磁性开关”,使得我们有“开”和“关”这两种状态,这个“开”和“关”表示的“1”和“0”,还可以作为后续线路的输入信号,让我们开始可以通过最简单的电路,来组合形成我们需要的逻辑。
通过这些线圈和开关,我们也可以很容易地创建出 “与(AND)”“或(OR)”“非(NOT)”这样的逻辑。我们在输入端的电路上,提供串联的两个开关,只有两个开关都打开,电路才接通,输出的开关也才能接通,这其实就是模拟了计算机里面的“与”操作。
在输入端的电路,提供两条独立的线路到输出端,两条线路上各有一个开关,那么任何一个开关打开了,到输出端的电路都是接通的,这其实就是模拟了计算机中的“或”操作。
把输出端的“螺旋线圈 + 磁性开关”的组合,从默认关掉,只有通电有了磁场之后打开,换成默认是打开通电的,只有通电之后才关闭,就得到了一个计算机中的“非”操作。输出端开和关正好和输入端相反。这个在数字电路中,也叫作反向器(Inverter)。

6、浮点数
用科学计数法来表示实数。浮点数的科学计数法的表示,有一个 IEEE 的标准,它定义了两个基本的格式。一个是用 32 比特表示单精度的浮点数,也就是 float 或者 float32 类型。另外一个是用 64 比特表示双精度的浮点数,也就是 double 或者 float64 类型。

单精度的 32 个比特可以分成三部分。
第一部分是一个符号位,用来表示是正数还是负数。一般用 s 来表示。在浮点数里,不像正数分符号数还是无符号数,所有的浮点数都是有符号的。
接下来是一个 8 个比特组成的指数位。一般用 e 来表示。8 个比特能够表示的整数空间,就是 0~255。在这里用 1~254 映射到 -126~127 这 254 个有正有负的数上。因为浮点数,不仅仅想要表示很大的数,还希望能够表示很小的数,所以指数位也会有负数。
最后,是一个 23 个比特组成的有效数位。我们用 f 来表示。
回到浮点数的加法过程,其中指数位较小的数,需要在有效位进行右移,在右移的过程中,最右侧的有效位就被丢弃掉了。这会导致对应的指数位较小的数,在加法发生之前,就丢失精度。两个相加数 的指数位差的越大,位移的位数越大,可能丢失的精度也就越大。当然,也有可能右移丢失的有效位都是 0。这种情况下,对应的加法虽然丢失了需要加的数字的精度,但是因为对应的值都是 0,实际的加法的数值结果不会有精度损失。
一个常见的应用场景是,在一些“积少成多”的计算过程中,比如在机器学习中,经常要计算海量样本计算出来的梯度或者 loss,于是会出现几亿个浮点数的相加。每个浮点数可能都差不多大,但是随着累积值的越来越大,就会出现“大数吃小数”的情况。
可以做一个简单的实验,用一个循环相加 2000 万个 1.0f,最终的结果会是 1600 万左右,而不是 2000 万。这是因为,加到 1600 万之后的加法因为精度丢失都没有了。这个代码比起上面的使用 2000 万来加 1.0 更具有现实意义。
public class FloatPrecision { public static void main(String[] args) { float sum = 0.0f; for (int i = 0; i < 20000000; i++) { float x = 1.0f; sum += x; } System.out.println("sum is " + sum); } }
结果:sum is 1.6777216E7
面对这个问题,具体的解决办法。一种叫作�Kahan Summation的算法来解决这个问题。
public class KahanSummation { public static void main(String[] args) { float sum = 0.0f; float c = 0.0f; for (int i = 0; i < 20000000; i++) { float x = 1.0f; float y = x - c; float t = sum + y; c = (t-sum)-y; sum = t; } System.out.println("sum is " + sum); } }
结果:sum is 2.0E7
这个算法的原理其实并不复杂,就是在每次的计算过程中,都用一次减法,把当前加法计算中损失的精度记录下来,然后在后面的循环中,把这个精度损失放在要加的小数上,再做一次运算。
