牛客多校第8场 A题

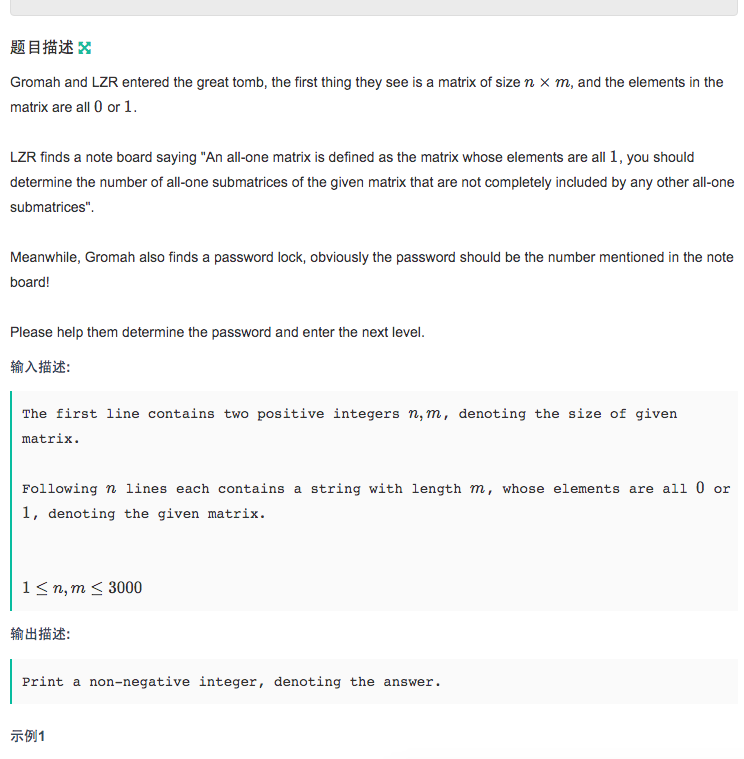
这个题也很奇妙，也是在一个简单模型上面做一点点更改，然后就可以得出答案，算一道很妙的题目了，个人觉得应该是铜牌把关题的那种，如果做得快的话说不定能拿银牌

显然我们得遍历所有矩阵，但是这个矩阵可以有奇妙的方法遍历，我们可以利用信息保存，减少一些不必要的运算来保存。然后得出答案。

下面就是我们通过枚举下届，然后通过这个下届我们先缓存一下高度，对这个高度进行操作。

这个过程我们可以通过单调栈来处理，单调栈本身就是用来处理一些矩形的面积，计数的东东，在它的运行过程它会把当前高度的最大面积都计算出来，这个自然是最妙的。。。。。。。。。这个可以保证当前是对的

那我们怎么能保证下面是对的呢，如果下面不是满的1的话那么这就是唯一的，这个应该是挺好想的。

然后考虑如果高度相同，显然只有一个计数，这时候应当把这个也考虑进去，这个相同高度取最大就ok

下面是代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <stack>
#include <cmath>
typedef long long ll;
using namespace std;
const int maxn=3100;
int n,m;
char s[maxn][maxn];
int hi[maxn][maxn];
int sum[maxn][maxn];
int ai[maxn],siz[maxn];
int ans=0;

void solve(int k){
    stack<int> sta; sta.push(0);
    for(int i=1;i<=m+1;i++){
        if(ai[i]>ai[sta.top()]){
            sta.push(i);
        }else{
            int len=0;
            while(!sta.empty()&&ai[i]<=ai[sta.top()]){
                if(ai[i]==ai[sta.top()]){
                    len+=siz[sta.top()];
                    sta.pop();continue;
                }
                len+=siz[sta.top()];
                int l=i-len,r=i-1;
                if(sum[k+1][r]-sum[k+1][l-1]!=(r-l+1)){
                    ans++;
                }
                sta.pop();
            }
            sta.push(i);siz[i]=len+1;
        }
    }
}


int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%s",s[i]+1);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            hi[i][j]=s[i][j]=='1'?hi[i-1][j]+1:0;
            sum[i][j]=sum[i][j-1]+(s[i][j]=='1');
        }
    }

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++) ai[j]=hi[i][j];
        for(int j=1;j<=m;j++) siz[j]=1;
        ai[0]=0;ai[m+1]=0;
        solve(i);
    }
    printf("%d
",ans);
    return 0;
}