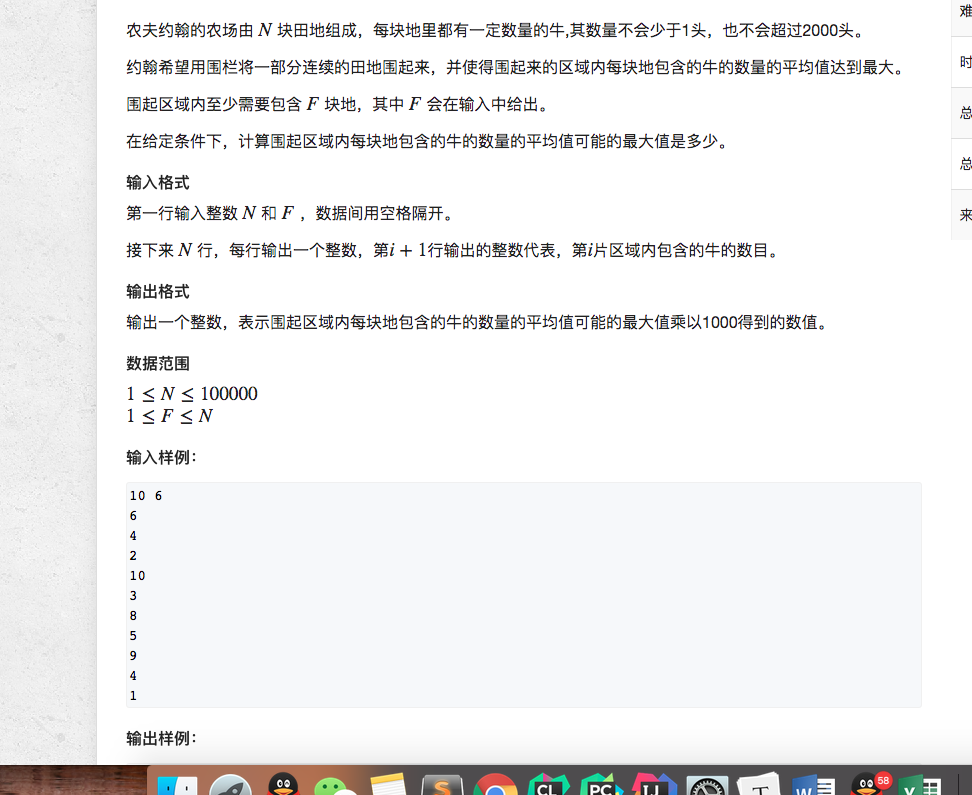
首先: (1): 这个*1000的操作肯定是为了防止出现double,这样的话都是整数,好操作!!!!!!
(2): 这个首先从暴力方向来想,我们要知道这个的值的话,我们的方法好像只有枚举所有大于等于F的区间来进行操作,但是这样的复杂度是O(N^2-F^2),这个可以等效看作是N^2的,只要数据稍微大一点点,这个算法就会被卡掉
(3): 然后这个可以接受的数据范围是Nlog(N)的?
(4): 每块地的平均值最大? 那么这个函数肯定是单调递增的,我们可以二分一个值来验证,看看这个值是不是符合规则的,如果符合规则,再二分更大的范围,如果这个值大了的话,就继续往小的值的方向走,如果合适的话就看能不能变大点。
(5):这个不是重点,二分的重点是我们想怎么去check这个值。二分+验证
(6): 二分+验证(这里面最重要是验证,怎么把一个直接求值的问题转换成验证性问题,这个是重中之重)(二分的话我们有时候也会碰到一些单调性很难证明或者单调性直接就是萎了的算法)
(7): 我们考虑一下怎么来做这倒题,首先转化成一个二分问题,哪我们怎么来验证?怎么来check呢》????? 不可能对每个端再枚举然后相减把,这样除了多了个log外没有任何用处
(8): 我们二分的是最后的答案,那对这个答案我们可以怎么操作呢。我们二分的是这个平均值mid ,这个显然可以知道 有 sum[i]-sum[j-1]-(i-j+1)*mid 我们发现这样不好搞,把每个num[i]减去mid,这个就可以把mid放进sum里面去。就可以得到我们最后的答案了。
下面是代码:

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <iostream> 5 #include <cmath> 6 #include <bitset> 7 typedef long long ll; 8 using namespace std; 9 const int maxn=101000; 10 ll num[maxn],sum[maxn],ai[maxn]; 11 int n,f; 12 ll lb=1000,rb=1,ans=0; 13 // sum[i]-sum[j-1] > 0 说明至少能有这么多 14 bool check(ll mid){ 15 sum[0]=0; 16 for(int i=1;i<=n;i++) ai[i]=num[i]-mid; 17 for(int i=1;i<=n;i++) sum[i]=sum[i-1]+ai[i]; 18 ll minn=sum[0]; 19 for(int i=f;i<=n;i++){ 20 if(sum[i]>=minn) return true; 21 minn=min(sum[i-f+1],minn); 22 } 23 return false; 24 } 25 26 int main(){ 27 scanf("%d%d",&n,&f); 28 for(int i=1;i<=n;i++){scanf("%lld",&num[i]);num[i]=num[i]*1000;rb+=num[i];} 29 while(lb<=rb){ 30 ll mid=(lb+rb)/2; 31 if(check(mid)){ 32 ans=mid; 33 lb=mid+1; 34 }else rb=mid-1; 35 } 36 printf("%lld ",ans); 37 return 0; 38 }
