使用Scikit Learn的分类器探索Iris数据集

作者|Dehao Zhang
编译|VK
来源|Towards Data Science

暂时，想象一下你不是一个花卉专家（如果你是专家，那对你很好！）。你能区分三种不同的鸢尾属植物吗？刚毛鸢尾属，花色鸢尾属和维吉尼亚鸢尾属（setosa, versicolor, virginica）？

我知道我不能…

但是，如果我们有一个包含这些物种实例的数据集，以及它们的萼片和花瓣的测量结果呢？

换言之，我们能从这个数据集中学到什么来帮助我们区分这三个物种吗？

---

目录

1. 我们为什么选择这个数据集？

2. 我们想回答什么问题？

3. 在这个数据集中我们能找到什么？

4. 我们正在构建哪些分类器？

5. 下一步该怎么办？

数据集

在这篇博文中，我将探索UCI机器学习库中的Iris数据集。它摘自其网站，据说这可能是模式识别文献中最著名的数据库。此外，Jason Brownlee，机器学习社区创建者，他称该数据集为机器学习的“Hello World”。

我将把这个数据集推荐给那些对数据科学感兴趣并渴望构建第一个ML模型的人。它的一些优良特性见下文：

• 150个具有4个属性的实例（相同的单位，全部为数字）

• 均衡的阶级分布

• 无缺失数据

如你所见，这些特性有助于将你在数据准备过程中花费的时间减至最少，这样你就可以专注于构建你的第一个ML模型。

并不是说准备阶段不重要。相反，这个过程是如此的重要，以至于对于一些初学者来说，这可能是非常耗时的，而且他们在开始模型开发之前可能会把自己压得喘不过气来。

例如，来自Kaggle的流行数据集House Prices:Advanced returnation Techniques有大约80个特征，其中超过20%包含某种程度的缺失数据。在这种情况下，你可能需要花费一些时间来理解属性并填充缺失的值。

---

目标

在研究了这个数据集之后，我们希望能够回答两个问题，这在分类问题中非常典型：

1. 预测-给定新的数据点，模型预测其类（物种）的准确度如何？
2. 推断-哪些预测因素可以有效地帮助预测？

---

分类

分类是一类有监督的机器学习问题，其中目标（响应）变量是离散的。给定包含已知标签的训练数据，分类器从输入变量（X）到输出变量（Y）近似一个映射函数（f）。

现在是时候写一些代码了！请参阅我的Github页面以获取完整的Python代码（在Jupyter Notebook中编写）。

链接：https://github.com/terryz1/explore-iris

---

导入库并加载数据集

首先，我们需要导入库：pandas（加载数据集）、numpy（矩阵操作）、matplotlib和seaborn（可视化）以及sklearn（构建分类器）。在导入它们之前，请确保它们已经安装（请参阅此处的安装程序包指南）。

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from pandas.plotting import parallel_coordinates
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn import metrics
from sklearn.naive_bayes import GaussianNB
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis, QuadraticDiscriminantAnalysis
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression

要加载数据集（也可以在我的Github页面中找到），我们可以使用pandas的read_csv函数（我的代码还包括通过url加载的选项）。

data = pd.read_csv('data.csv')

加载数据后，我们可以通过head查看前几行：

data.head(5)

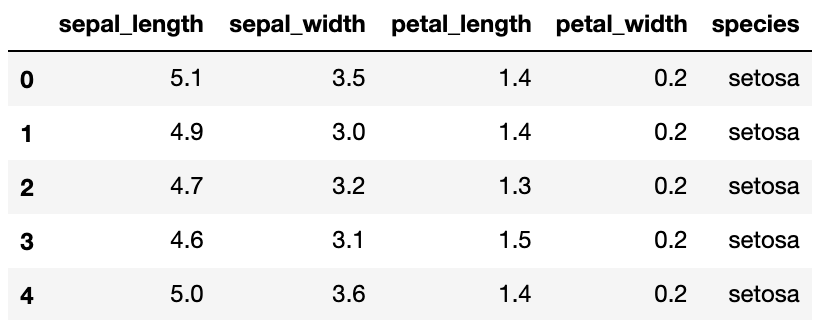
注：所有四个测量单位均为厘米。

数值摘要

首先，让我们通过“describe”来查看每个属性的数值摘要：

data.describe()

我们还可以使用groupby和size检查类分布：

data.groupby('species').size()

我们可以看到每个类都有相同数量的实例。

训练集测试集拆分

现在，我们可以将数据集分成训练集和测试集。通常，我们还应该有一个验证集，用来评估每个分类器的性能，进行微调，并确定最佳模型。测试集主要用于报告。然而，由于这个数据集的规模很小，我们可以通过使用测试集来满足验证集的目的来简化它。

此外，我还使用了分层保持方法来估计模型精度。我会在以后的博客中讨论减少偏差的方法。

train, test = train_test_split(data, test_size = 0.4, stratify = data[‘species’], random_state = 42)

注意：我设置了40%的数据作为测试集，以确保有足够的数据点来测试模型。

探索性数据分析

在我们分割数据集之后，我们可以继续探索训练数据。matplotlib和seaborn都有很好的绘图工具，我们可以用来可视化。

让我们首先创建一些单变量图。为每个特征创建直方图：

n_bins = 10
fig, axs = plt.subplots(2, 2)
axs[0,0].hist(train['sepal_length'], bins = n_bins);
axs[0,0].set_title('Sepal Length');
axs[0,1].hist(train['sepal_width'], bins = n_bins);
axs[0,1].set_title('Sepal Width');
axs[1,0].hist(train['petal_length'], bins = n_bins);
axs[1,0].set_title('Petal Length');
axs[1,1].hist(train['petal_width'], bins = n_bins);
axs[1,1].set_title('Petal Width');

# 添加一些间距
fig.tight_layout(pad=1.0);

请注意，对于花瓣长度和花瓣宽度，似乎有一组数据点的值比其他数据点小，这表明此数据中可能存在不同的组。

接下来，让我们尝试一些箱线图：

fig, axs = plt.subplots(2, 2)
fn = ["sepal_length", "sepal_width", "petal_length", "petal_width"]
cn = ['setosa', 'versicolor', 'virginica']
sns.boxplot(x = 'species', y = 'sepal_length', data = train, order = cn, ax = axs[0,0]);
sns.boxplot(x = 'species', y = 'sepal_width', data = train, order = cn, ax = axs[0,1]);
sns.boxplot(x = 'species', y = 'petal_length', data = train, order = cn, ax = axs[1,0]);
sns.boxplot(x = 'species', y = 'petal_width', data = train,  order = cn, ax = axs[1,1]);
# 添加一些间距
fig.tight_layout(pad=1.0);

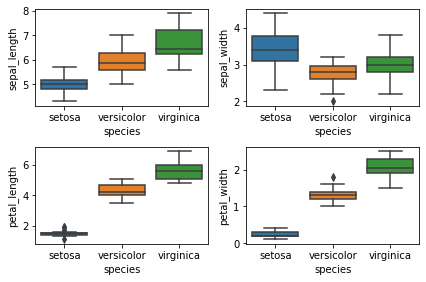
底部的两个图表明我们前面看到的那组数据点是setosas。它们的花瓣尺寸比其他两个物种更小，分布也更少。与其他两个物种相比，versicolor的平均值比virginica 低。

小提琴图是另一种可视化方式，它结合了直方图和方框图的优点：

sns.violinplot(x="species", y="petal_length", data=train, size=5, order = cn, palette = 'colorblind');

现在我们可以使用seaborn的pairplot函数绘制所有成对属性的散点图：

sns.pairplot(train, hue="species", height = 2, palette = 'colorblind');

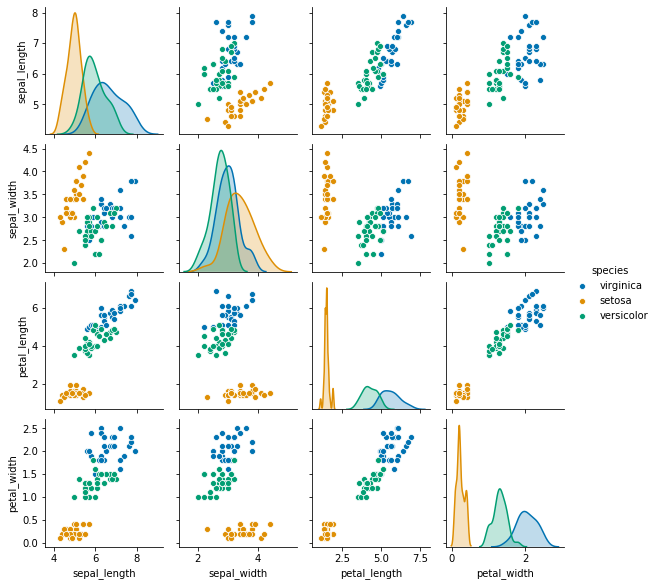
请注意，有些变量似乎高度相关，例如花瓣长度和花瓣宽度。另外，花瓣的测量比萼片的分离更好。

接下来，我们制作一个相关矩阵来定量检查变量之间的关系：

corrmat = train.corr()
sns.heatmap(corrmat, annot = True, square = True);

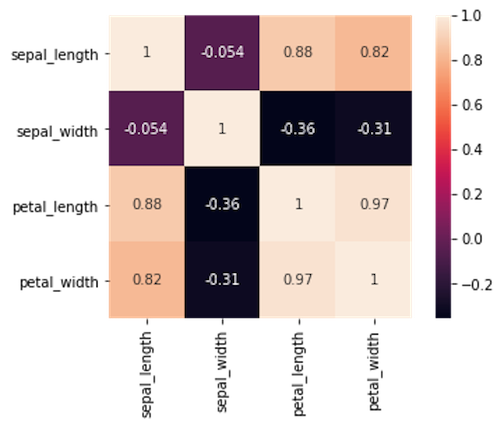
主要的结论是花瓣的大小有高度的正相关，而萼片的测量是不相关的。注意花瓣特征与萼片长度也有较高的相关性，但与萼片宽度无关。

另一个很酷的可视化工具是 parallel coordinate plot，它将每一行表示为一条直线。

parallel_coordinates(train, "species", color = ['blue', 'red', 'green']);

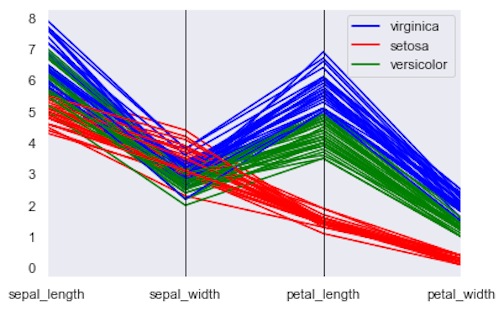
正如我们之前所见，花瓣的测量比萼片的能更好地区分物种。

---

构建分类器

现在我们准备建立一些分类器

为了让我们的生活更轻松，让我们把类标签和特征分开：

X_train = train[['sepal_length','sepal_width','petal_length','petal_width']]
y_train = train.species
X_test = test[['sepal_length','sepal_width','petal_length','petal_width']]
y_test = test.species

决策树

我想到的第一个分类器是一个称为决策树。原因是我们可以看到分类规则，而且很容易解释。

让我们使用sklearn（文档）构建一个，最大深度为3，我们可以在测试数据上检查它的准确性：

mod_dt = DecisionTreeClassifier(max_depth = 3, random_state = 1)
mod_dt.fit(X_train,y_train)
prediction=mod_dt.predict(X_test)
print(‘The accuracy of the Decision Tree is’,”{:.3f}”.format(metrics.accuracy_score(prediction,y_test)))

--------------------------------------------------------------------
The accuracy of the Decision Tree is 0.983.

决策树正确预测了98.3%的测试数据。该模型的一个优点是，你可以通过每个因子的feature-importances属性来查看其特征重要性：

mod_dt.feature_importances_

--------------------------------------------------------------------
array([0.        , 0.        , 0.42430866, 0.57569134])

从输出结果和基于四个特征的索引，我们知道前两个特征（萼片度量）并不重要，只有花瓣特征被用来构建这棵树。

决策树的另一个优点是我们可以通过plot_tree可视化分类规则：

plt.figure(figsize = (10,8))
plot_tree(mod_dt, feature_names = fn, class_names = cn, filled = True);

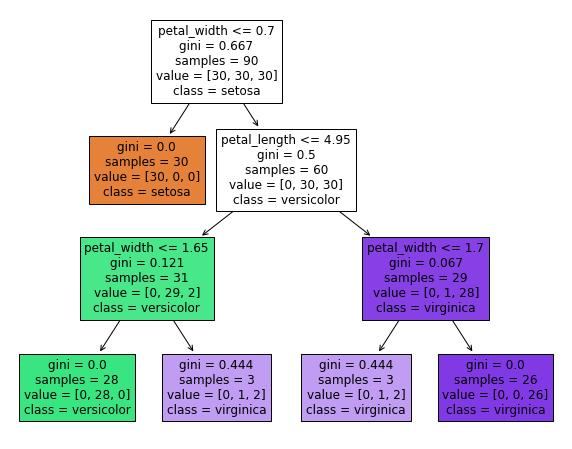
此树中的分类规则（对于每个拆分，左->是，右->否）

除了每个规则（例如，第一个标准是花瓣宽度≤0.7），我们还可以看到每个拆分、指定类别等的基尼指数。请注意，除了底部的两个“浅紫色”框外，所有终端节点都是纯的。对于这两类情况，表示没有信心。

为了证明对新数据点进行分类是多么容易，假设一个新实例的花瓣长度为4.5cm，花瓣宽度为1.5cm，那么我们可以根据规则预测它是versicolor。

由于只使用花瓣特征，因此我们可以可视化决策边界并以二维形式绘制测试数据：

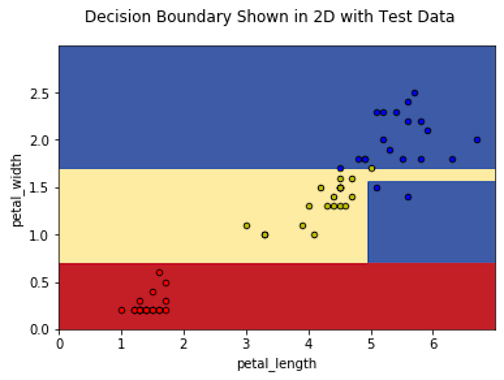
在60个数据点中，59个被正确分类。另一种显示预测结果的方法是通过混淆矩阵：

disp = metrics.plot_confusion_matrix(mod_dt, X_test, y_test,
                                 display_labels=cn,
                                 cmap=plt.cm.Blues,
                                 normalize=None)
disp.ax_.set_title('Decision Tree Confusion matrix, without normalization');

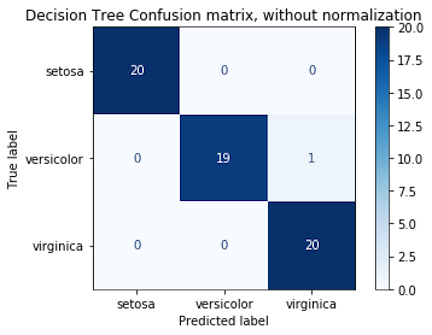
通过这个矩阵，我们看到有一种花色，我们预测是virginica。

构建一棵树的一个缺点是它的不稳定性，这可以通过诸如随机森林、boosting等集成技术来改善。现在，让我们继续下一个模型。

高斯朴素贝叶斯分类器

最流行的分类模型之一是朴素贝叶斯。它包含了“Naive”一词，因为它有一个关键的类条件独立性假设，这意味着给定的类，每个特征的值都被假定独立于任何其他特征的值（请参阅此处）。

我们知道，这里显然不是这样，花瓣特征之间的高度相关性证明了这一点。让我们用这个模型来检查测试精度，看看这个假设是否可靠：

The accuracy of the Guassian Naive Bayes Classifier on test data is 0.933

如果我们只使用花瓣特征，结果如何：

The accuracy of the Guassian Naive Bayes Classifier with 2 predictors on test data is 0.950

有趣的是，仅使用两个特征会导致更正确的分类点，这表明在使用所有特征时可能会过度拟合。看起来我们朴素贝叶斯分类器做得不错。

线性判别分析

如果我们使用多元高斯分布来计算类条件密度，而不是使用一元高斯分布的乘积（在朴素贝叶斯中使用），我们将得到一个LDA模型。LDA的关键假设是类之间的协方差相等。我们可以使用所有特征和仅花瓣特征检查测试精度：

The accuracy of the LDA Classifier on test data is 0.983
The accuracy of the LDA Classifier with two predictors on test data is 0.933

使用所有特征可以提高我们的LDA模型的测试精度。

为了在二维可视化决策边界，我们可以仅使用花瓣的LDA模型，并绘制测试数据：

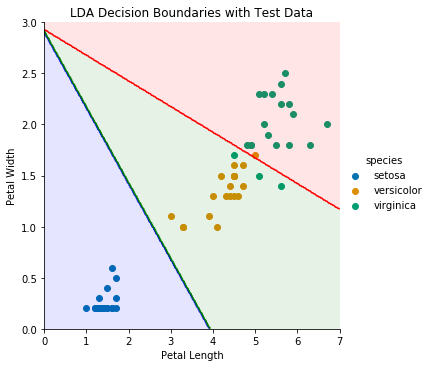
四个测试点被错误分类-三个virginica和一个versicolor。

现在假设我们要用这个模型对新的数据点进行分类，我们只需在图上画出点，然后根据它所属的颜色区域进行预测。

二次判别分析

LDA和QDA的区别在于QDA不假设类间的协方差相等，它被称为“二次型”，因为决策边界是一个二次函数。

The accuracy of the QDA Classifier is 0.983
The accuracy of the QDA Classifier with two predictors is 0.967

在所有特征的情况下，它与LDA具有相同的精度，并且仅使用花瓣时，它的性能稍好一些。

类似地，让我们绘制QDA（只有花瓣的模型）的决策边界：

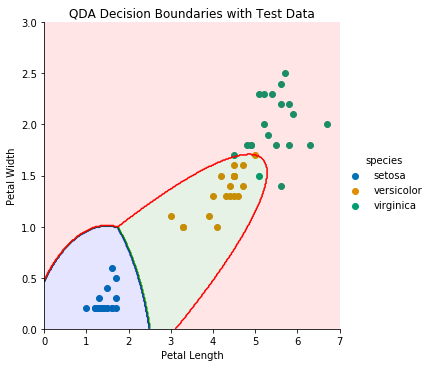
KNN分类器

现在，让我们换个角度，看看一个名为KNN的非参数模型。它是一个十分流行的模型，因为它相对简单和易于实现。然而，我们需要意识到当特征的数量变大时我们会受到维度诅咒。

让我们用K的不同选择绘制测试精度：

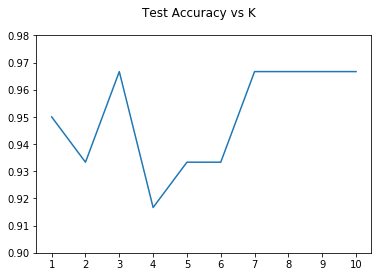
我们可以看到，当K为3或在7到10之间时，精确度最高(约为0.965)。与以前的模型相比，分类新的数据点不那么直接，因为我们需要在四维空间中观察它的K个最近的邻居。

其他模型

我还研究了其他模型，如logistic回归、支持向量机分类器等。

注意SVC（带线性内核）的测试精度达到了100%！

我们现在应该很有信心，因为我们的大多数模型的准确率都超过了95%。

---

下一步

以下是一些未来研究的想法：

• 对这些模型进行交叉验证，并比较它们之间的平均精确度。

• 找到其他数据源，包括其他鸢尾属物种及其萼片/花瓣测量值（如果可能，也包括其他属性），并检查新的分类精度。

• 制作一个交互式的web应用程序，根据用户输入的测量值来预测物种。

结尾

我们研究了Iris数据集，然后使用sklearn构建了一些流行的分类器。我们发现花瓣的测量值比萼片的测量值更有助于分类实例。此外，大多数模型的测试精度都在95%以上。

参考文献

• Dua, D. and Graff, C. (2019). UCI Machine Learning Repository [http://archive.ics.uci.edu/ml]. Irvine, CA: University of California, School of Information and Computer Science.
• Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani. (2013). An introduction to statistical learning : with applications in R. New York :Springer.

原文链接：https://towardsdatascience.com/exploring-classifiers-with-python-scikit-learn-iris-dataset-2bcb490d2e1b

欢迎关注磐创AI博客站：
http://panchuang.net/

sklearn机器学习中文官方文档：
http://sklearn123.com/

欢迎关注磐创博客资源汇总站：
http://docs.panchuang.net/