深入理解卷积网络的卷积

卷积神经网络是一种特殊的神经网络结构，是自动驾驶汽车、人脸识别系统等计算机视觉应用的基础，其中基本的矩阵乘法运算被卷积运算取代。它们专门处理具有网格状拓扑结构的数据。例如，时间序列数据和图像数据可以看作是一个二维像素网格。

历史

卷积神经网络最初是由福岛核电站在1980年引入的，当时名为Neocognitron。它的灵感来自于Hubel和Weisel提出的神经系统的层次模型。但由于其复杂的无监督学习算法，即无监督学习，该模型并不受欢迎。1989年，Yann LeCun利用反向传播和Neocognitron的概念提出了一种名为LeNet的架构，该架构被美国和欧洲用于手写的邮政编码识别。邮政服务。Yann LeCun进一步研究了这个项目，最终在1998年发布了LeNet-5——第一个引入了我们今天在CNN仍然使用的一些基本概念的现代卷积神经网络。他还发布了MNIST手写数字数据集，这可能是机器学习中最著名的基准数据集。在20世纪90年代，计算机视觉领域转移了它的焦点，许多研究人员停止了对CNN架构的研究。神经网络的研究经历了一个寒冷的冬天，直到2012年，多伦多大学的一组研究人员在著名的ImageNet挑战赛中进入了一个基于CNN的模型(AlexNet)，最终以16.4%的错误率赢得了比赛。此后，卷积神经网络不断向前发展，基于CNN的体系结构不断赢得ImageNet, 2015年，基于卷积神经网络的体系结构ResNet的误差率超过人类水平的5.1%，误差率为3.57%。

卷积的误称

在CNN中广泛使用的卷积运算是用词不当的。严格地说，所使用的操作是相关，而不是卷积。这两个操作符都有一点不同，我们将分别讨论它们，以理解它们之间的区别。

互相关

相关是在图像上移动滤波掩码(通常称为核)并计算每个位置的乘积和的过程。相关是滤波器位移的函数。换句话说，相关的第一个值对应滤波器的零位移，第二个值对应一个位移，以此类推。

数学公式:

图3给出了使用F滤波器与图像I的一维互相关运算的数学公式。假设F具有奇数个元素会很方便，因此我们可以假设F随其中心移动。我们说F有2N 1的元素,这些索引从-N到N,F(0)是中心元素。

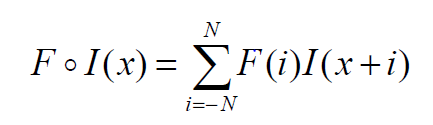
类似地，我们可以将这个概念扩展到下图所示的2d情况。基本思想是一样的，除了图像和滤波器现在是2D。我们可以假设我们的滤波器有奇数个元素，所以它由一个(2N 1)x(2N 1)矩阵表示。

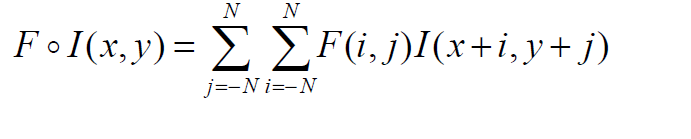
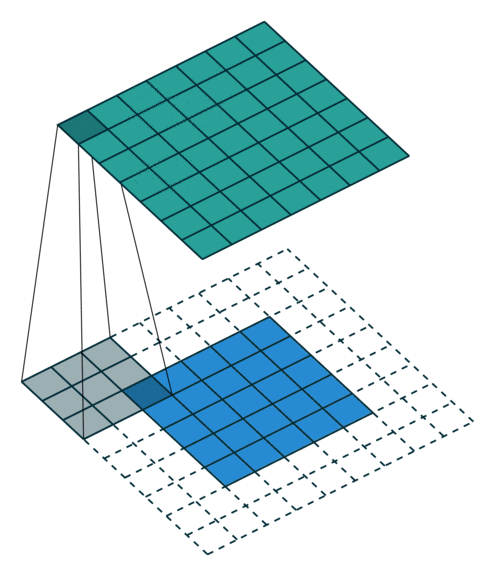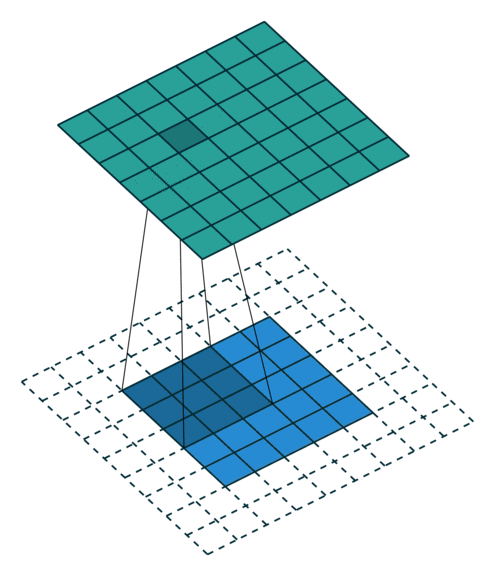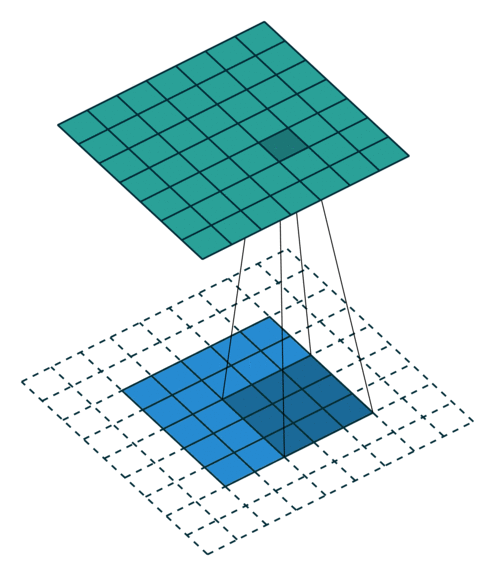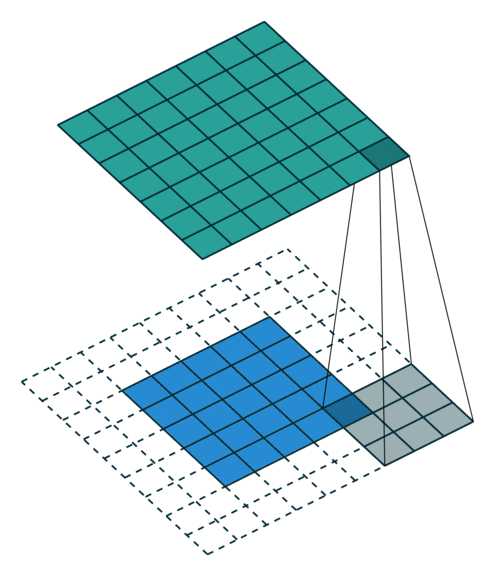
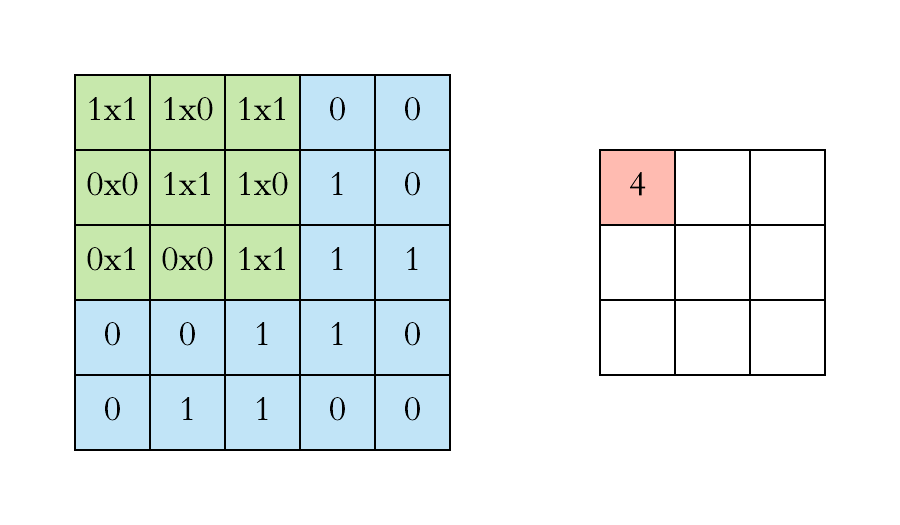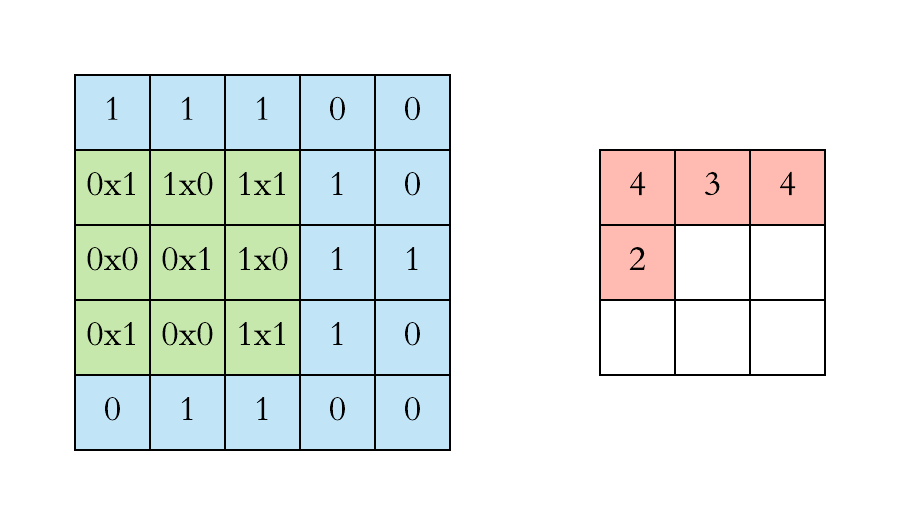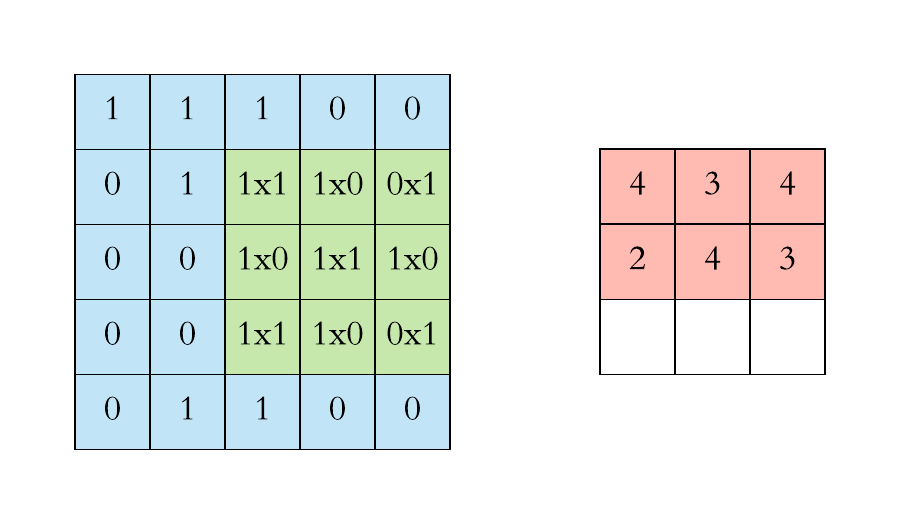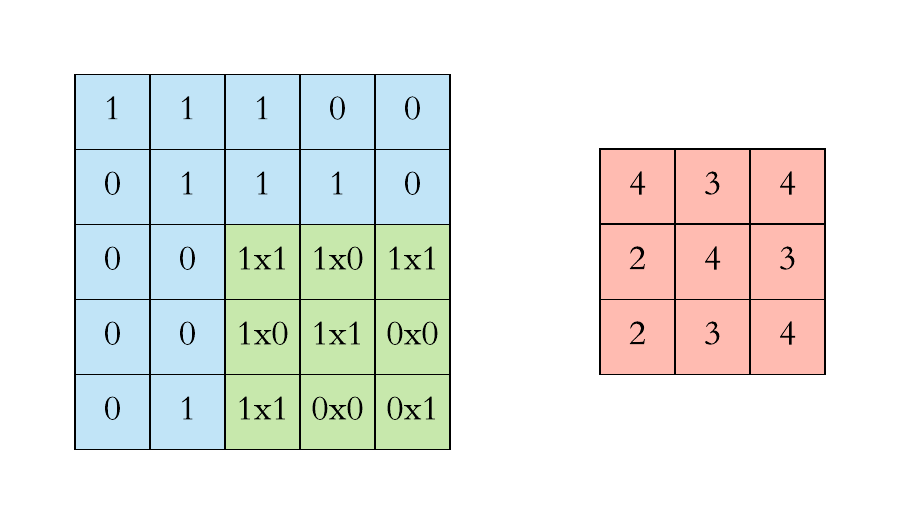
二维的相关运算非常简单。我们只是取一个给定大小的滤波器，然后把它放在与滤波器大小相同的图像的一个局部区域上。我们继续这个操作，在整个图像中移动相同的滤波器。这也帮助我们实现了两个非常受欢迎的属性:

1. 平移不变性:我们的视觉系统应该感知、响应或检测相同的物体，而不管它出现在图像的什么地方。
2. 局部性:我们的视觉系统聚焦于局部区域，而不考虑图像的其他部分发生了什么。

互相关函数具有一个特性，当它应用于离散的单位脉冲(一个二维矩阵，其中只有一个1，其他都是0)时，得到的结果是滤波器的副本，但旋转了180度。

卷积:

卷积运算与互相关运算非常相似，但有细微的区别。在卷积运算中，首先将核翻转180度，然后应用于图像。卷积的基本性质是将一个核与一个离散的单位脉冲进行卷积，在脉冲的位置上得到一个核的拷贝。

我们在互相关部分看到，一个互相关操作产生一个脉冲的拷贝，但是旋转了180度。因此，如果我们预先旋转滤波器并执行相同的乘积滑动和运算，我们应该能够得到期望的结果。

数学公式:
利用核函数F对图像I进行的卷积运算由一维的公式给出。卷积就像相关一样，只是我们在互相关之前先把滤波器翻转一下

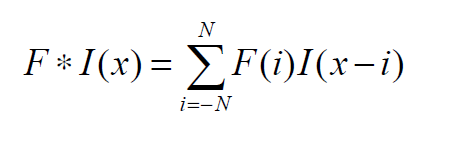
在二维卷积的情况下，我们水平和垂直翻转滤波器。这可以写成:

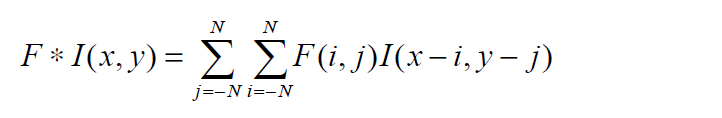
卷积运算同样遵循平移不变性和局部性的性质。

注意:
尽管这两个操作稍有不同，但是所使用的核是否对称并不重要。

结论:

在这篇文章中，我们简要讨论了卷积神经网络的历史和一些特性。我们讨论了卷积这个错误的说法，即在各种文本中经常提到的卷积运算其实是互相关运算。这种差别很细微，但却很有用，每个进入、练习或经验丰富的计算机视觉领域的人都应该知道。

引用

1. Deep Learning book by Ian Goodfellow and Yoshua Bengio and Aaron Courville.
2. Digital Image Processing by Rafael C. Gonzalez.
3. Dive into Deep Learning by Aston Zhang, Zack C. Lipton, Mu Li and Alex J. Smola.
4. Correlation and Convolution by David Jacobs.
5. Figure 9 taken from https://towardsdatascience.com/applied-deep-learning-part-4-convolutional-neural-networks-584bc134c1e2.
6. https://spatial-lang.org/conv
7. The meme is taken from 7. https://www.mihaileric.com/posts/convolutional-neural-networks/.

欢迎关注磐创博客资源汇总站：
http://docs.panchuang.net/

欢迎关注PyTorch官方中文教程站：
http://pytorch.panchuang.net/

OpenCV中文官方文档：
http://woshicver.com/