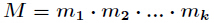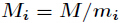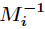BGV方案


SIMD技术



中国剩余定理
在《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二(除以3余2),五五数之剩三(除以5余3),七七数之剩二(除以7余2),问物几何?”这个问题称为“孙子问题”,该问题的一般解法国际上称为“中国剩余定理”。
简单点说就是求x,使其满足:![]()
我们的主要求解方法分为三步:
- 找出三个数:从3和5的公倍数中找出被7除余1的最小数15,从3和7的公倍数中找出被5除余1 的最小数21,最后从5和7的公倍数中找出除3余1的最小数70。
- 用15乘以2(2为最终结果除以7的余数),用21乘以3(3为最终结果除以5的余数),同理,用70乘以2(2为最终结果除以3的余数),然后把三个乘积相加(15*2+21*3+70*2)得到和233。
- 用233除以3,5,7三个数的最小公倍数105,得到余数23,即233%105=23。这个余数23就是符合条件的最小数。
算法分析
我们将“孙子问题”拆分成几个简单的小问题,从零开始,试图揣测古人是如何推导出这个解法的。
首先,我们假设n1是满足除以3余2的一个数,比如2,5,8等等,也就是满足3*k+2(k>=0)的一个任意数。同样,我们假设n2是满足除以5余3的一个数,n3是满足除以7余2的一个数。
有了前面的假设,我们先从n1这个角度出发,已知n1满足除以3余2,能不能使得 n1+n2 的和仍然满足除以3余2?进而使得n1+n2+n3的和仍然满足除以3余2?
这就牵涉到一个最基本数学定理,如果有a%b=c,则有(a+kb)%b=c(k为非零整数),换句话说,如果一个除法运算的余数为c,那么被除数与k倍的除数相加(或相减)的和(差)再与除数相除,余数不变。这个是很好证明的。
以此定理为依据,如果n2是3的倍数,n1+n2就依然满足除以3余2。同理,如果n3也是3的倍数,那么n1+n2+n3的和就满足除以3余2。这是从n1的角度考虑的,再从n2,n3的角度出发,我们可推导出以下三点:
- 为使n1+n2+n3的和满足除以3余2,n2和n3必须是3的倍数。
- 为使n1+n2+n3的和满足除以5余3,n1和n3必须是5的倍数。
- 为使n1+n2+n3的和满足除以7余2,n1和n2必须是7的倍数。
因此,为使n1+n2+n3的和作为“孙子问题”的一个最终解,需满足:
- n1除以3余2,且是5和7的公倍数。
- n2除以5余3,且是3和7的公倍数。
- n3除以7余2,且是3和5的公倍数。
所以,孙子问题解法的本质是从5和7的公倍数中找一个除以3余2的数n1,从3和7的公倍数中找一个除以5余3的数n2,从3和5的公倍数中找一个除以7余2的数n3,再将三个数相加得到解。在求n1,n2,n3时又用了一个小技巧,以n1为例,并非从5和7的公倍数中直接找一个除以3余2的数,而是先找一个除以3余1的数,再乘以2。
这里又有一个数学公式,如果a%b=c,那么(a*k)%b=a%b+a%b+…+a%b=c+c+…+c=kc(k>0),也就是说,如果一个除法的余数为c,那么被除数的k倍与除数相除的余数为kc。展开式中已证明。
最后,我们还要清楚一点,n1+n2+n3只是问题的一个解,并不是最小的解。如何得到最小解?我们只需要从中最大限度的减掉3,5,7的公倍数105即可。道理就是前面讲过的定理“如果a%b=c,则有(a-kb)%b=c”。所以(n1+n2+n3)%105就是最终的最小解。
总结
经过分析发现,中国剩余定理的孙子解法就是以下两个基本数学定理的灵活运用:
- 如果 a%b=c , 则有 (a+kb)%b=c (k为非零整数)。
- 如果 a%b=c,那么 (a*k)%b=kc (k为大于零的整数)。
扩展算法
设正整数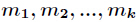 两两互素,则同余方程组
两两互素,则同余方程组
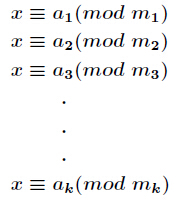
有整数解。并且在模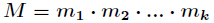 下的解是唯一的,解为
下的解是唯一的,解为
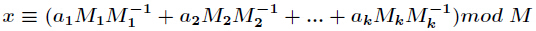

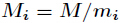 ,而
,而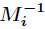 为
为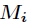 模
模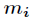 的逆元。
的逆元。
代码:
int CRT(int a[],int m[],int n)
{
int M = 1;
int ans = 0;
for(int i=1; i<=n; i++)
M *= m[i];
for(int i=1; i<=n; i++)
{
int x, y;
int Mi = M / m[i];
extend_Euclid(Mi, m[i], x, y);
ans = (ans + Mi * x * a[i]) % M;
}
if(ans < 0) ans += M;
return ans;
}
多项式中国剩余定理



求乘法逆元
有两种方法:
1、费马小定理
该方法速度非常快

求逆元代码:
#include <stdio.h>
#include <math.h>
int main()
{
int m, n, x;
puts(" 基于费马定理求逆元
");
puts(" 对m * x = 1 mod n,求x
");
printf("请输入m=");
scanf("%d", &m);
printf("请输入n=");
scanf("%d", &n);
x = (int)pow(m, n - 2) % n;
printf("x=%d
", x);
system("pause");
return 0;
}
2、扩展欧几里得

扩展欧几里得算法实现:
#include<iostream>
using namespace std;
//递归求解
int exgcd(int a, int b, int& x, int& y)
{
if (b == 0)
{
x = 1;
y = 0;
return a;
}
int gcd = exgcd(b, a % b, x, y);
int x2 = x, y2 = y;
x = y2;
y = x2 - (a / b) * y2;
return gcd;
}
//非递归求解
int exgcd01(int a, int b, int& x, int& y)
{
int x1, y1, x0, y0;
x0 = 1; y0 = 0;
x1 = 0; y1 = 1;
x = 0; y = 1;
int r = a % b;
int q = (a - r) / b;
while (r)
{
x = x0 - q * x1; y = y0 - q * y1;
x0 = x1; y0 = y1;
x1 = x; y1 = y;
a = b; b = r; r = a % b;
q = (a - r) / b;
}
return b;
}
int main()
{
int x, y, a, b,option;
cout << "扩展欧几里得算法" << endl;
cout << endl << "请选择:1、递归求解;2、非递归求解" << endl;
cin >> option;
if (option == 1)
{
cout << "请输入a和b:" << endl;
cin >> a >> b;
cout << "a和b的最大公约数:" << endl;
cout << exgcd(a, b, x, y) << endl;
cout << "ax+by=gcd(a,b) 的一组解是:" << endl;
cout << x << " " << y << endl;
}
else if (option == 2)
{
cout << "请输入a和b:" << endl;
cin >> a >> b;
cout << "a和b的最大公约数:" << endl;
cout << exgcd01(a, b, x, y) << endl;
cout << "ax+by=gcd(a,b) 的一组解是:" << endl;
cout << x << " " << y << endl;
}
else
cout << "请重新输入!" << endl;
return 0;
}
求逆元算法实现:请参考 求逆元
参考
1、云外包密文查询和计算研究-全韩彧
3、扩展欧几里得算法
6、多项式的 “中国剩余定理”-包志超