转载:【1】
什么是递归?
如果在函数中存在着调用函数本身的情况,这种现象就叫递归
以阶层函数为例,如下, 在 factorial 函数中存在着 factorial(n - 1) 的调用,所以此函数是递归函数:
public int factorial(int n) { if (n < =1) { return 1; } return n * factorial(n - 1) }
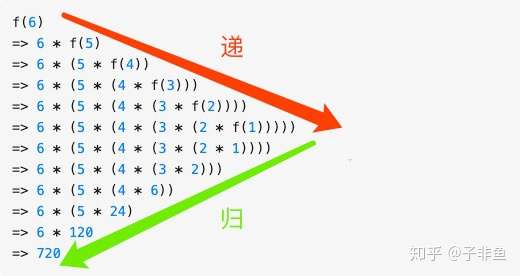
求解问题 f(6), 由于 f(6) = n * f(5), 所以 f(6) 需要拆解成 f(5) 子问题进行求解,同理 f(5) = n * f(4) ,也需要进一步拆分,... ,直到 f(1), 这是「递」,f(1) 解决了,由于 f(2) = 2 f(1) = 2 也解决了,.... f(n)到最后也解决了,这是「归」,所以递归的本质是能把问题拆分成具有相同解决思路的子问题,。。。直到最后被拆解的子问题再也不能拆分,解决了最小粒度可求解的子问题后,在「归」的过程中自然顺其自然地解决了最开始的问题。
递归解题思路
递归有以下两个特点:
- 一个问题可以分解成具有相同解决思路的子问题,子子问题,换句话说这些问题都能调用同一个函数
- 经过层层分解的子问题最后一定是有一个不能再分解的固定值的(即终止条件),如果没有的话,就无穷无尽地分解子问题了,问题显然是无解的。
所以解递归题的关键在于我们首先需要根据以上递归的两个特点判断题目是否可以用递归来解。
经过判断可以用递归后,接下来我们就来看看用递归解题的基本套路(四步曲):1. 先定义一个函数,明确这个函数的功能,由于递归的特点是问题和子问题都会调用函数自身,所以这个函数的功能一旦确定了, 之后只要找寻问题与子问题的递归关系即可2. 接下来寻找问题与子问题间的关系(即递推公式),这样由于问题与子问题具有相同解决思路,只要子问题调用步骤 1 定义好的函数,问题即可解决。所谓的关系最好能用一个公式表示出来,比如 f(n) = n * f(n-) 这样,如果暂时无法得出明确的公式,用伪代码表示也是可以的, 发现递推关系后,要寻找最终不可再分解的子问题的解,即(临界条件),确保子问题不会无限分解下去。由于第一步我们已经定义了这个函数的功能,所以当问题拆分成子问题时,子问题可以调用步骤 1 定义的函数,符合递归的条件(函数里调用自身)3. 将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中4. 最后也是很关键的一步,根据问题与子问题的关系,推导出时间复杂度,如果发现递归时间复杂度不可接受,则需转换思路对其进行改造,看下是否有更靠谱的解法
实例
求阶乘
输入一个正整数n,输出n!的值。其中n!=123…n
1、定义这个函数,明确这个函数的功能,我们知道这个函数的功能是求 n 的阶乘, 之后求 n-1, n-2 的阶乘就可以调用此函数了
/**
* 求 n 的阶乘
*/
public int factorial(int n) {
}
2.寻找问题与子问题的关系 阶乘的关系比较简单, 我们以 f(n) 来表示 n 的阶乘, 显然 f(n) = n * f(n - 1), 同时临界条件是 f(1) = 1
3.将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中
/** * 求 n 的阶乘 */ public int factorial(int n) { // 第二步的临界条件 if (n < =1) { return 1; } // 第二步的递推公式 return n * factorial(n-1) }
4.求时间复杂度 由于 f(n) = n * f(n-1) = n * (n-1) * .... * f(1),总共作了 n 次乘法,所以时间复杂度为 n。
青蛙跳台阶
一只青蛙可以一次跳 1 级台阶或者一次跳 2 级台阶,例如:
跳上第 1 级台阶只有一种跳法:直接跳 1 级即可。 跳上第 2 级台阶有两种跳法:每次跳 1 级,跳两次;或者一次跳 2 级。 问要跳上第 n 级台阶有多少种跳法?
/** * 跳 n 极台阶的跳法 */ public int f(int n) { }
2.寻找问题与子问题之前的关系 这两者之前的关系初看确实看不出什么头绪,但仔细看题目,一只青蛙只能跳一步或两步台阶,自上而下地思考,也就是说如果要跳到 n 级台阶只能从 n-1 或 n-2 级跳, 所以问题就转化为跳上 n-1 和 n-2 级台阶的跳法了,如果 f(n) 代表跳到 n 级台阶的跳法,那么从以上分析可得 f(n) = f(n-1) + f(n-2),显然这就是我们要找的问题与子问题的关系,而显然当 n = 1, n = 2, 即跳一二级台阶是问题的最终解,于是递推公式系为:
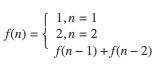
3.将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中补充后的函数如下:
/** * 跳 n 极台阶的跳法 */ public int f(int n) { if (n == 1) return 1; if (n == 2) return 2; return f(n-1) + f(n-2) }
4.计算时间复杂度
由以上的分析可知
f(n) 满足以下公式:
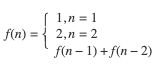
斐波那契的时间复杂度计算涉及到高等代数的知识, 这里不做详细推导,有兴趣的同学可以点击这里查看,我们直接结出结论
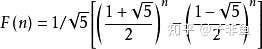
由些可知时间复杂度是指数级别,显然不可接受,那回过头来看为啥时间复杂度这么高呢,假设我们要计算 f(6),根据以上推导的递归公式,展示如下:
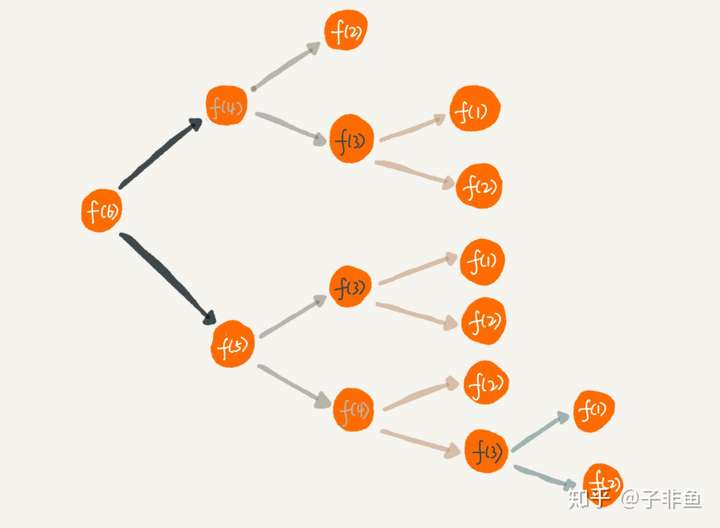
可以看到有大量的重复计算, f(3) 计算了 3 次, 随着 n 的增大,f(n) 的时间度自然呈指数上升了
5.优化 既然有这么多的重复计算,我们可以想到把这些中间计算过的结果保存起来,如果之后的计算中碰到同样需要计算的中间态,直接在这个保存的结果里查询即可,这就是典型的以空间换时间,改造后的代码如下
public int f(int n) { if (n == 1) return 1; if (n == 2) return 2; // map 即保存中间态的键值对, key 为 n,value 即 f(n) if (map.get(n)) { return map.get(n) } return f(n-1) + f(n-2) }
那么改造后的时间复杂度是多少呢,由于对每一个计算过的 f(n) 我们都保存了中间态,不存在重复计算的问题,所以时间复杂度是 O(n), 但由于我们用了一个键值对来保存中间的计算结果,所以空间复杂度是 O(n)。问题到这里其实已经算解决了,但身为有追求的程序员,我们还是要问一句,空间复杂度能否继续优化?
5.使用循环迭代来改造算法 我们在分析问题与子问题关系(f(n) = f(n-1) + f(n-2))的时候用的是自顶向下的分析方式,但其实我们在解 f(n) 的时候可以用自下而上的方式来解决,通过观察我们可以发现以下规律:
f(1) = 1 f(2) = 2 f(3) = f(1) + f(2) = 3 f(4) = f(3) + f(2) = 5 .... f(n) = f(n-1) + f(n-2)
最底层 f(1), f(2) 的值是确定的,之后的 f(3), f(4) ,...等问题都可以根据前两项求解出来,一直到 f(n)。所以我们的代码可以改造成以下方式:
public int f(int n) { if (n == 1) return 1; if (n == 2) return 2; int result = 0; int pre = 1; int next = 2; for (int i = 3; i < n + 1; i ++) { result = pre + next; pre = next; next = result; } return result; }
改造后的时间复杂度是 O(n), 而由于我们在计算过程中只定义了两个变量(pre,next),所以空间复杂度是O(1)
简单总结一下: 分析问题我们需要采用自上而下的思维,而解决问题有时候采用自下而上的方式能让算法性能得到极大提升,思路比结论重要!
反转二叉树
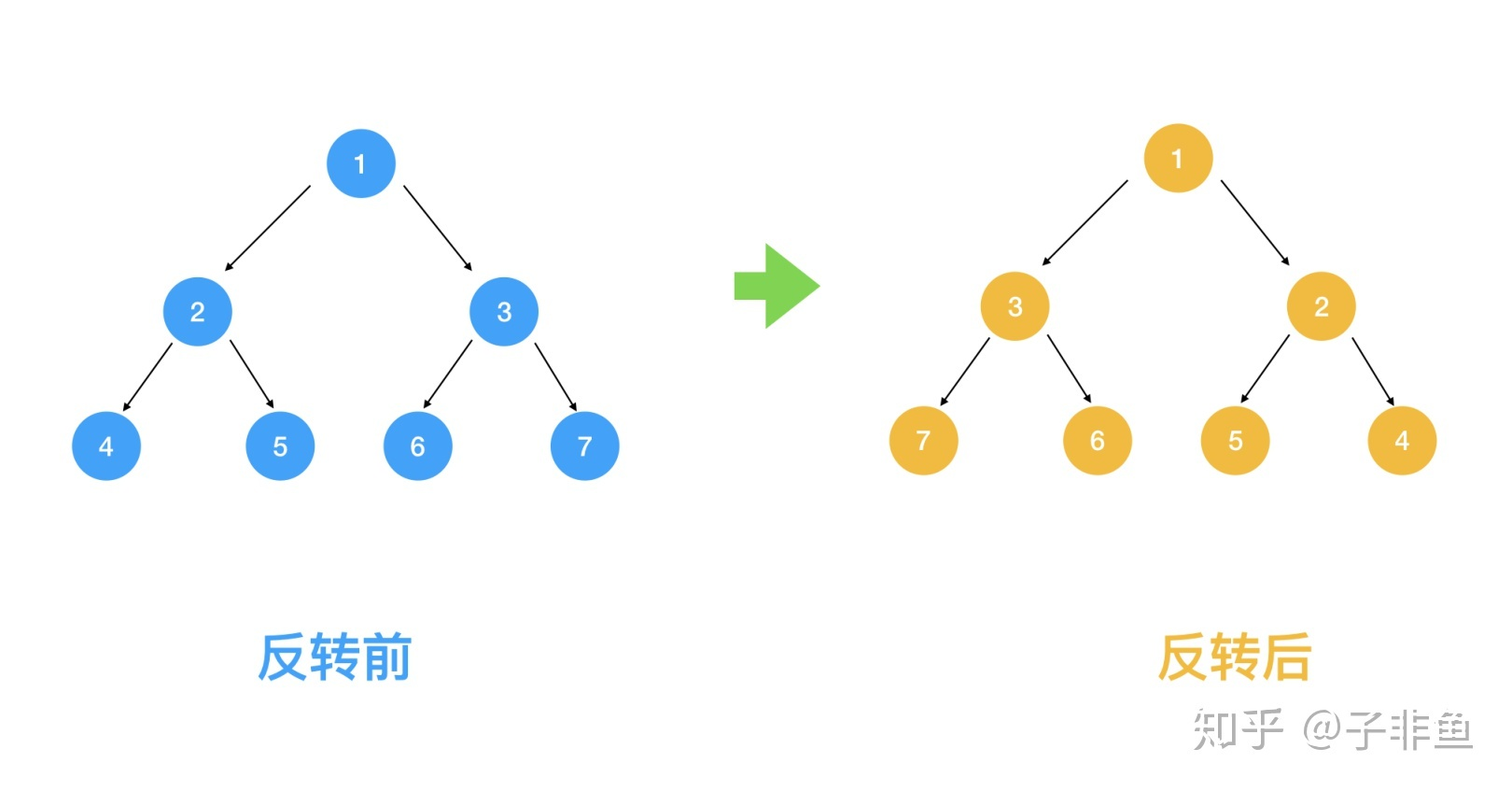
将左边的二叉树反转成右边的二叉树
1.定义一个函数,这个函数代表了翻转以 root 为根节点的二叉树:
public static class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } } public TreeNode invertTree(TreeNode root) { }
2.查找问题与子问题的关系,得出递推公式 我们之前说了,解题要采用自上而下的思考方式,那我们取前面的1, 2,3 结点来看,对于根节点 1 来说,假设 2, 3 结点下的节点都已经翻转,那么只要翻转 2, 3 节点即满足需求
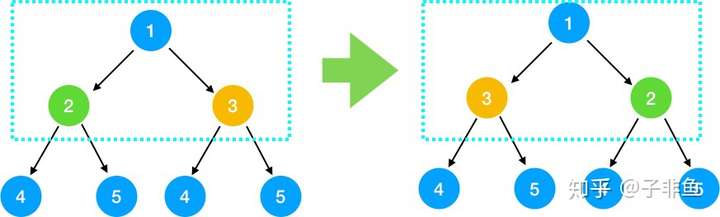
对于2, 3 结点来说,也是翻转其左右节点即可,依此类推,对每一个根节点,依次翻转其左右节点,所以我们可知问题与子问题的关系是 翻转(根节点) = 翻转(根节点的左节点) + 翻转(根节点的右节点) 即 invert(root) = invert(root->left) + invert(root->right)
而显然递归的终止条件是当结点为叶子结点时终止(因为叶子节点没有左右结点)
3.将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中
public TreeNode invertTree(TreeNode root) { // 叶子结果不能翻转 if (root == null) { return null; } // 翻转左节点下的左右节点 TreeNode left = invertTree(root.left); // 翻转右节点下的左右节点 TreeNode right = invertTree(root.right); // 左右节点下的二叉树翻转好后,翻转根节点的左右节点 root.right = left; root.left = right; return root; }
TreeNode left = invertTree(root.left);
从根节点出发不断对左结果调用翻转函数, 直到叶子节点,每调用一次都会压栈,左节点调用完后,出栈,再对右节点压栈....,下图可知栈的大小为3, 即树的高度,如果是完全二叉树 ,则树的高度为logn, 即空间复杂度为O(logn),
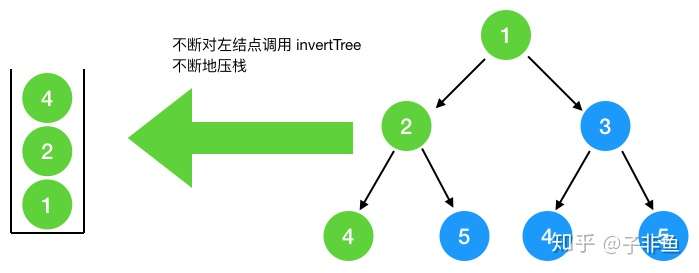
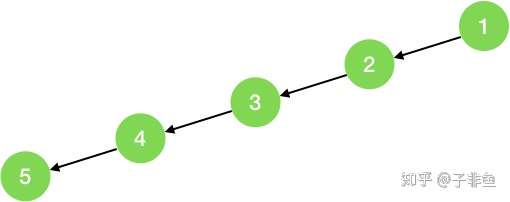
最坏情况,如果此二叉树是如图所示(只有左节点,没有右节点),则树的高度即结点的个数 n,此时空间复杂度为 O(n),总的来看,空间复杂度为O(n)
汉诺塔

移动规则:

分析:
move函数是一个递归函数,功能是:把x上n个圆盘移动到z上
代码:
#include <stdio.h>
#include <stdlib.h>
// 汉诺塔递归
void main()
{
int i,n;
printf("请指定有几层:
");
scanf("%d",&n);
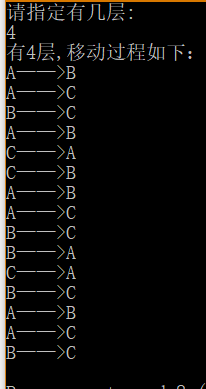
printf("有%d层,移动过程如下:
",n);
move(n,'A','B','C');
}
void move(int n,char x,char y,char z)
{
if(n < 0)
printf("输入错误,不成立!");
else if(n == 1)
printf("%c——>%c
",x,z);
else
{
move(n - 1,x,z,y);
printf("%c——>%c
",x,z);
move(n - 1,y,x,z);
}
}