TensorFlow 实例一（一元线性回归）

使用TensorFlow进行算法设计与训练的核心步骤：

• 准备数据
• 构建模型
• 训练模型
• 进行预测

问题描述：

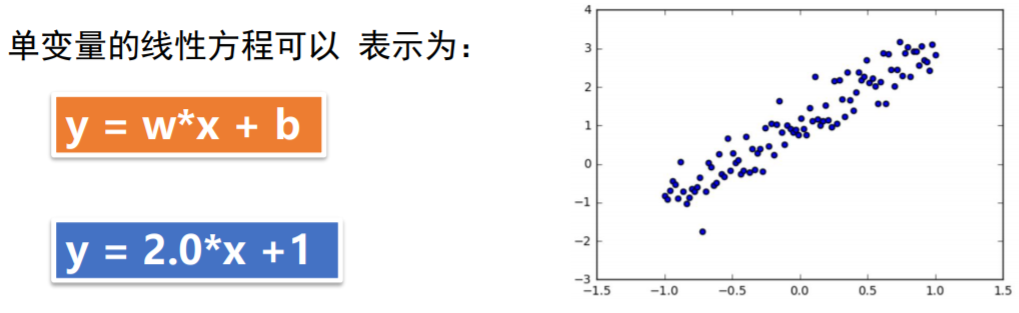
　　通过人工数据集，随机生成一个近似采样随机分布，使得w = 2.0 ，b= 1，并加入一个噪声，噪声的最大振幅是0.4

过程描述：

　　人工数据集生成

# 在JUpiter中，使用matplotlib 显示图像需要设置为 inline 模式，否则不会出现图像
%matplotlib inline

import matplotlib.pyplot as plt  #载入matplotlib 
import numpy as np    #载入numpy
import tensorflow as tf   #载入TensorFlow

# 设置随机数种子
np.random.seed(5)
#直接采用np 生成等差数列的方法，生成100个点，每一个点的取值在 -1~ 1之间
x_data = np.linspace(-1,1,100)

# y = 2x + 1 噪声，其中，噪声的维度与x_data一致
y_data = 2 * x_data + 1.0 +np.random.randn(*x_data.shape) * 0.4
　　#x_data.shape  是一个元组   * 加在变量前，拆分元组

　　利用matplotlib画出生成结果

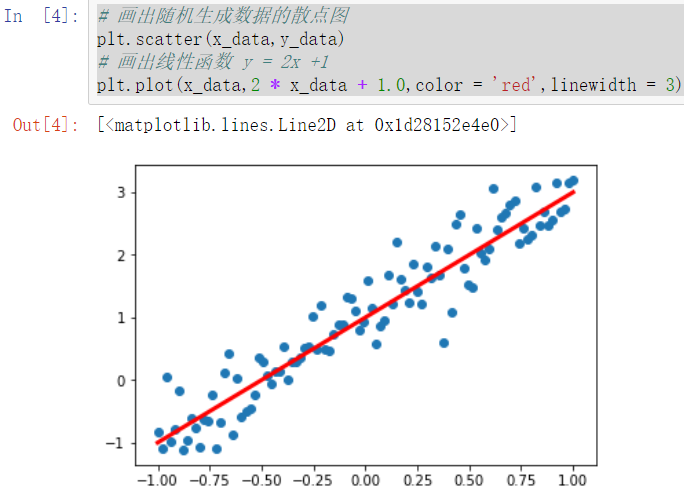
# 画出随机生成数据的散点图
plt.scatter(x_data,y_data)

# 画出线性函数 y = 2x +1
plt.plot(x_data,2 * x_data + 1.0,color = 'red',linewidth = 3)

　　构建模型

　　　　定义训练数据的占位符，x是特征值，y是标签：

　　　　定义模型函数：

x = tf.placeholder("float",name = "x")
y = tf.placeholder("float",name = "y")
def model(x,w,b):
    return tf.multiply(x,w) + b

　　　　创建变量：

　　　　　　TensorFlow变量的声明函数是tf.Variable

　　　　　　tf.Variable的作用是保存和更新参数

　　　　　　变量的初始值可以是随机数，常数，或者是通过其他的初始值计算得到的

#构建线性函数的斜率，变量w 
w = tf.Variable(2.0,name = "w0")
#构建线性函数的截距，变量b
b = tf.Variable(0.0,name = "b0")
#pred是预测值，向前计算
pred = model(x,w,b)

　　训练模型

　　　　设置训练参数：

# 迭代次数（训练次数）
train_epochs = 10
#学习率
learning_rate = 0.5

　　　   定义损失函数：

　　　　　   损失函数用于描述预测值与真实值之间的误差，从而指导模型收敛方向

　　　　　   常见损失函数：均方差和交叉熵

# 采样均方差作为损失函数
loss_function = tf.reduce_mean(tf.square(y - pred))

 　　　  定义优化器：

　　　　　　定义优化器Optimizer，初始化一个 GradientDescentOptimizer

　　　　　　设置学习率和优化目标：最小化损失  （每次迭代优化w和b）

# 梯度下降优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)

　　　　创建会话：

　　　　　　声明会话：

sess = tf.Session()

　　　　　　变量初始化：　　

 　　　　　　　　在执行前，需将所有的变量初始化，通过  tf.global_variables_initializer() 实现对所有变量初始化

init = tf.global_variables_initializer()
sess.run(init)

　　迭代训练

　　　　模型训练：设置迭代轮次，每次通过将样本逐个输入模型，进行梯度下降优化操作

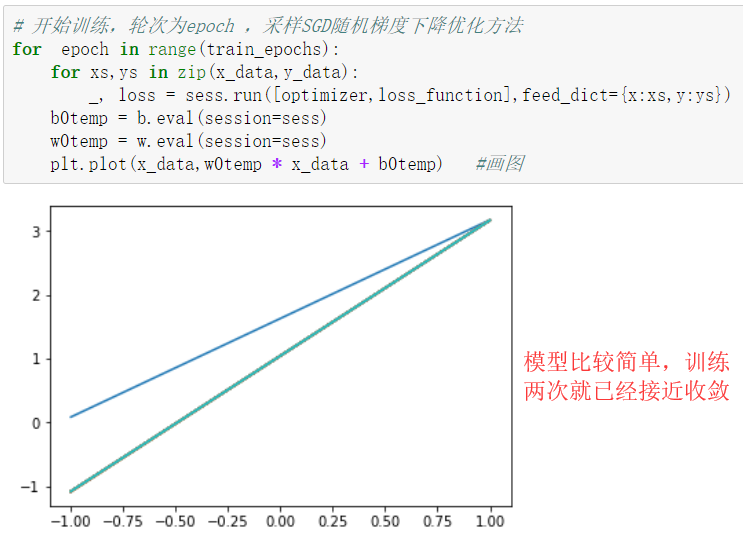
　　　　每次迭代后，绘制出模型曲线

# 开始训练，轮次为epoch ，采样SGD随机梯度下降优化方法
for  epoch in range(train_epochs):
    for xs,ys in zip(x_data,y_data):
        _, loss = sess.run([optimizer,loss_function],feed_dict={x:xs,y:ys})
    b0temp = b.eval(session=sess)
    w0temp = w.eval(session=sess)
    plt.plot(x_data,w0temp * x_data + b0temp)   #画图

　　打印训练参数

print("w:",sess.run(w)) #w的值应该在2附近
print("b:",sess.run(b)) # b的值应该在1附近

　　结果可视化

plt.scatter(x_data,y_data,label = 'Original data')
plt.plot(x_data,x_data * sess.run(w) + sess.run(b),label = 'Fitted line',color = 'r',linewidth = 3)
plt.legend(loc = 2) #通过参数loc指定图例位置

　　使用训练好的模型进行预测

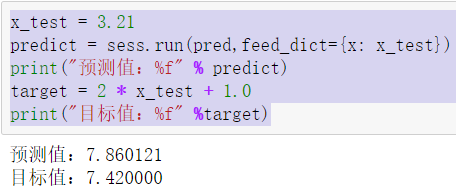
x_test = 3.21
predict = sess.run(pred,feed_dict={x: x_test})
print("预测值：%f" % predict)
target = 2 * x_test + 1.0
print("目标值：%f" %target)

过程补充

　　随机梯度下降：

在梯度下降法中， 批量指的是用于在单次迭代中计算梯度的样本总数

假定批量是指整个数据集，数据集通常包含很大样本（数万甚至数千亿），
此外， 数据集通常包含多个特征。因此，一个批量可能相当巨大。如果是超
大批量，则单次迭代就可能要花费很长时间进行计算

随机梯度下降法 ( SGD) 每次迭代只使用一个样本（批量大小为 1），如果
进行足够的迭代，SGD 也可以发挥作用。“随机”这一术语表示构成各个批
量的一个样本都是随机选择的

小批量随机梯度下降法（量 小批量 SGD）是介于全批量迭代与 SGD 之间的折
衷方案。小批量通常包含 10-1000 个随机选择的样本。小批量 SGD 可以减
少 SGD 中的杂乱样本数量，但仍然比全批量更高效

　　在训练中显示损失值：

# 在JUpiter中，使用matplotlib 显示图像需要设置为 inline 模式，否则不会出现图像
%matplotlib inline
import matplotlib.pyplot as plt  #载入matplotlib 
import numpy as np    #载入numpy
import tensorflow as tf   #载入TensorFlow
# 设置随机数种子
np.random.seed(5)
#直接采用np 生成等差数列的方法，生成100个点，每一个点的取值在 -1~ 1之间
x_data = np.linspace(-1,1,100)
# y = 2x + 1 噪声，其中，噪声的维度与x_data一致
y_data = 2 * x_data + 1.0 +np.random.randn(*x_data.shape) * 0.4

# 画出随机生成数据的散点图
plt.scatter(x_data,y_data)
# 画出线性函数 y = 2x +1
plt.plot(x_data,2 * x_data + 1.0,color = 'red',linewidth = 3)

x = tf.placeholder("float",name = "x")
y = tf.placeholder("float",name = "y")
def model(x,w,b):
    return tf.multiply(x,w) + b

#构建线性函数的斜率，变量w 
w = tf.Variable(2.0,name = "w0")
#构建线性函数的截距，变量b
b = tf.Variable(0.0,name = "b0")
#pred是预测值，向前计算
pred = model(x,w,b)

# 迭代次数（训练次数）
train_epochs = 10
#学习率
learning_rate = 0.5
# 采样均方差作为损失函数
loss_function = tf.reduce_mean(tf.square(y - pred))

# 梯度下降优化器
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

43 # 开始训练，轮数为epoch，采用SGD随机梯度下降优化方法
44 step = 0 # 记录训练步数
45 loss_list = []  #用于保存loss值的列表
46 display_step = 10
47 for epoch in range(train_epochs):
48     for xs,ys in zip(x_data,y_data):
49         _,loss = sess.run([optimizer,loss_function],feed_dict={x:xs,y:ys})
50         #显示损失值
51         #display_step ：控制报告的粒度
52             #例如：若display_step = 2，则将每训练2个样本输出依次损失粒度，与超参数不同，修改display_step 不会改变模型学习的规律
53         loss_list.append(loss)
54         step = step + 1
55         if step % display_step == 0:
56             print("训练次数:",'%02d' % (epoch + 1),"步数：%03d"%(step),"损失：","{:.9f}".format(loss))
57     b0temp = b.eval(session = sess)
58     w0temp = w.eval(session = sess)
59     plt.plot(x_data,w0temp * x_data +b0temp)  #画图

plt.plot(loss_list)  #图像化显示损失值

plt.plot(loss_list,'r+') #图像化显示损失值