推荐系统实战(一) —— UserCF

UserCF

 本系列文章主要介绍推荐系统领域相关算法原理及其实现。本文以项亮大神的《推荐系统实践》作为切入点，介绍推荐系统最基础的算法（可能也是最好用的）--基于用户的协同过滤算法(UserCF)。参考书中P44-50。

---

1.简述

假设在一个个性化的推荐系统中，用户A需要推荐，那么可以先找到与A有相似兴趣的用户，例如B、C、D把他们喜欢的，用户A没有听说过的物品推荐给A。这种方法被称为基于用户的协同过滤。

---

2.计算用户相似度

从算法原理中我们可以得到UserCF主要包括两个步骤：

1.找到和A用户兴趣相似的用户集合（B、C、D）。
2.找到这个集合中的用户喜欢，且目标用户A还未听说或购买过的物品推荐给目标用户。

步骤1.的关键其实就是计算用户兴趣的相似度。这里主要是利用用户行为来计算用户相似度。给定用户U和用户V，令N(u)，N(v)分别表示用户u，v曾经有正反馈的用户集合。用Jaccard公式计算：

[W_{uv} = frac{|N(u)igcap N(v)|}{|N(u)igcup N(v)|} ]

或者通过余弦相似度计算：

[W_{uv} = frac{|N(u)igcap N(v)|}{sqrt{|N(u)||N(v)|}} ]

以书中数据为例：

train = {'A':('a','b','d'),'B':('a','c'),'C':('b','e'),'D':('c','d','e')}

[W_{AB} = frac{|{a,b,d} igcap {a,c}|}{sqrt{|{a,b,d}||{a,c}|}} = frac{1}{sqrt{6}} ]

同理可计算Wac和Wad。
按书中对所有用户两两计算余弦相似度，时间复杂度是O(U*U)，在用户量很大时非常耗时，事实上，很多用户之间并没有对同样的物品产生过行为，因此可以先过滤出N(u)交N(v)不等于0的用户对(u,v)，然后再对其除以分母。
这里用item-user倒排表的方式，建立一个4*4的用户相似度矩阵C，最终得到的W[u][v]就是(u,v)对相似度的分子部分，再除以分母即可得到最终的用户相似度。如书中图2-7：

def UserSimilarity(train , IIF = False):
    # IIF 是否对 过于热门即 购买人数过于多的物品 在计算用户相似度的时候进行惩罚
    # 因为很多用户对之间并没有对相同的物品产生过行为，只计算对相同物品产生过行为的用户之间的相似度。
    # 采用余弦相似度
    # 建立倒排表，对每个物品保存只对其产生过行为的用户列表。
    item_users = dict() # 物品-用户 倒排表
    for u, items in train.items():
        for i in items:
            # 这里将 item_users.keys() 改为 item_users , 文中例子 应该用set 或 list存，而不是dict:
            if i not in item_users:
                item_users[i] = set()
            item_users[i].add(u)

    # 建立如图2-7所示的倒排矩阵
    C = dict() # key 用户对 value 购买同一物品的次数
    N = dict() # N(u) 表示用户购买的 商品数 {'A': 3, 'B': 2, 'C': 2, 'D': 3}
    for i,users in item_users.items():
        for u in users:
            if u not in N.keys():
                N[u] = 0
            N[u] += 1
            for v in users:
                if u == v:
                    continue
                if (u,v) not in C.keys():
                    C[u,v] = 0
                if IIF:
                    # len(users) 表示购买此物品的用户数，越热门，购买用户越多,C[u,v] 就越小
                    # 相当于之前的分子是相交个数，现在是
                    C[u,v] += 1 / math.log(1 + len(users))
                else:
                    C[u,v] += 1
    W = dict()
    for co_user, cuv in C.items():
        W[co_user] = cuv / math.sqrt(N[co_user[0]]*N[co_user[1]])
    
    return W

这里可以看下return的 W：

---

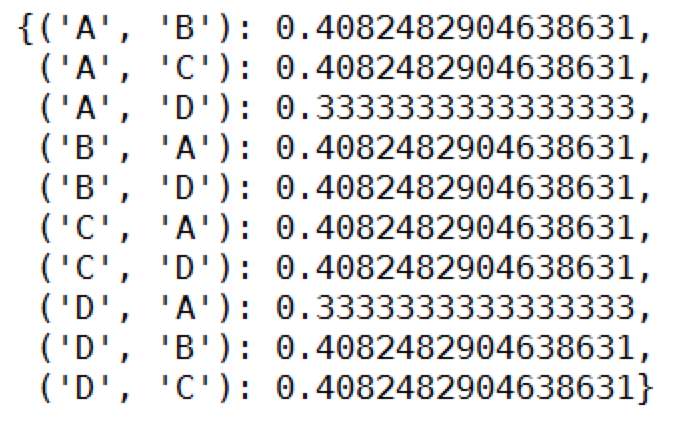
3.计算推荐结果

这里直接用书中P47的解释了，Wuv已经有了，其实就是根据W再乘一个权重r就可以了，r可以根据比如那些用户的行为更重要来改变，这里书中默认r都是1。

下述是推荐部分的代码：

def UserCFRecommend(user,train,W,k):
    # rvi 代表用户v对物品i的权重
    rvi = 1 
    rank = dict()
    interacted_items = train[user]
    related_user=[]
    # 和 A 有相似度的用户 ，B,C,D
    for co_user,sim in W.items():
        if co_user[0] == user:S
            related_user.append((co_user[1],sim))
    # v : 有相似度的用户 , wuv : 用户间相似度 
    for v , wuv in sorted(related_user , key = lambda a:a[1], reverse = True)[0:k]:
        for item in train[v]:
            if item in interacted_items:
                continue
            else:
                # 还是得初始化，才可以赋值
                if item not in rank.keys():
                    rank[item] = 0 
                rank[item] += wuv*rvi
    return rank

最后选择对A进行推荐，K取3，由于A对a，b，d有过行为，K=3又代表相似用户为B，C，D，所以会将c、e推荐给A。这里得到：

和书中结果一致。在书中对用户相似度的改进也在上述UserSimilarity部分的代码中体现了，只需在计算W的时候将参数 IIF=True 即可。该改进其实就是在计算u，v相似度时，对其进行惩罚，惩罚是基于在倒排表中所有购买此物品的用户长度，即此物品购买人数越多，提供的相似度越小，具体理解请参考代码。

代码详见：https://github.com/Alarical/Recommend/tree/master/UserCF

对于书中，表2-4 UserCF在movielens数据集中的运用，主要参考https://blog.csdn.net/u012050154/article/details/52268057大神的博客和代码，对与其代码增加了部分注释，详见我的github。

参考资料：

https://blog.csdn.net/guanbai4146/article/details/78016778
https://blog.csdn.net/u012050154/article/details/52268057
项亮 --《推荐系统实践》