优先队列——左式堆

【0】README

0.1） 本文文字描述部分转自 数据结构与算法分析， 旨在理解 优先队列——左式堆 的基础知识； 
0.2） 本文核心思路均为原创， 源代码部分借鉴 数据结构与算法分析 ； 
0.3） for original source code, please visit https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter6/p145_leftist_heap

1）相关定义

• 1.1）零路径长度定义： 到没有两个儿子的节点最短距离， 即零路径长Npl 定义为 从 X 到一个没有两个儿子的 节点的最短路径的长；也即， 非叶子节点到叶子节点的最少边数，其中NULL的零路径长为-1， 叶子节点的零路径长为0；（干货——零路径长的定义—— 非叶子节点到叶子节点的最少边数，非常重要，因为左式堆的定义是基于零路径长的定义的） 
  

• 1.２）左式堆定义：一棵具有堆序性质的二叉树　＋　零路径长：左儿子 ≧ 右儿子　＋　父节点 = min{儿子} +1；（干货——左式堆的定义是建立在具有堆序性的二叉树上，而不是二叉堆上）

2）merge操作原则： 根值大的堆与根值小的堆的右子堆合并；（干货——merge操作原则） 
3）merge操作存在的三种情况（设堆H1的根值小于H2）

• case1） H1只有一个节点；
• case2） H1根无右孩子；
• case3） H1根有右孩子；

---

补充（Complementary）：左式堆合并操作详解（merge）

左式堆合并原则：大根堆H2与小根堆H1的右子堆合并 （干货——左式堆合并原则） 
具体分三种情况（设堆H1的根值小于H2） 

• case1）H1只有一个节点（只有它自己而已）： H1只有一个节点，若出现不满足 零路径长：左儿子≧右儿子，交换左右孩子； 
   
  
  • Attention）上例中（中间所示堆），左儿子的零路径长为-1， 而右儿子的零路径长为0，所以不满足左式堆的条件， 需要交换左右孩子；
• case2）H1根无右孩子： H1根无右孩子，若出现不满足：零路径长：左儿子≧右儿子，需要交换左右孩子。 
   
  
  • Attention）上例中（中间所示堆），左儿子的零路径长为0， 而右儿子的零路径长为1，所以不满足左式堆的条件，需要交换；
• case3）H1根有右孩子： 
  
  • step1）截取H1的右子堆R1， 和截取H2的右子堆R2；
  • step2）将R1 与 R2进行merge操作得到H3， 且取R1和R2中较小根作为新根； （Attention： 现在你将看到，截取后的H1 和 H2， 以及新生成的H3 都是 case2）；
  • step3）比较H3的左右孩子，是否满足左式堆要求，如果不满足则交换左右孩子；
  • step4）将H3与没有右子堆的H1进行merge操作，也即最后将case3 转换为了 case2； 
     
    

Conclusion） 现在才知道，左式堆的merge操作其实是一个递归的过程， 看如下解析； （干货——这是最后解析merge操作啦）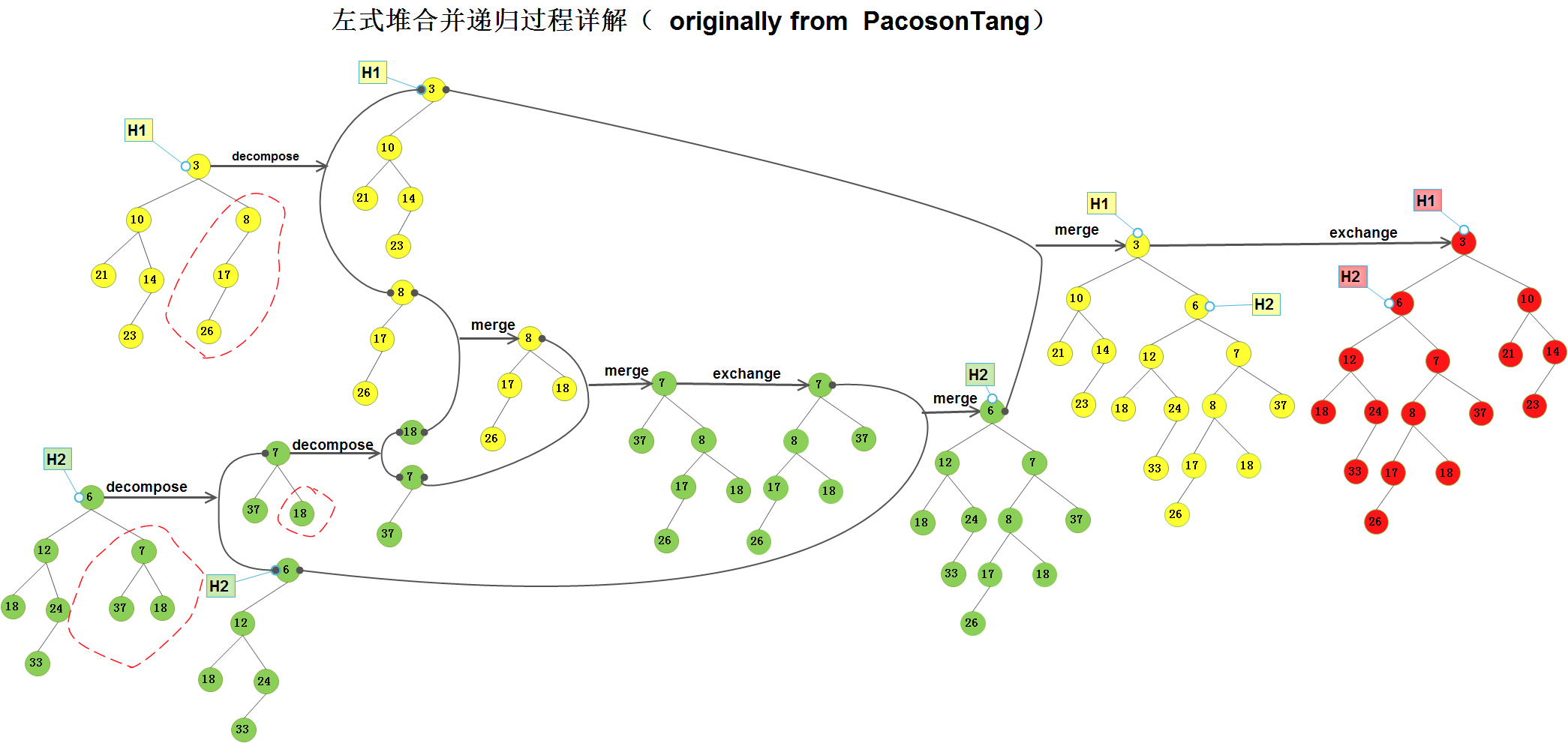 

Attention once again）

• A1）左式堆是建立在具有堆序性的二叉树上；
• A2）左式堆是建立在零路径长上；
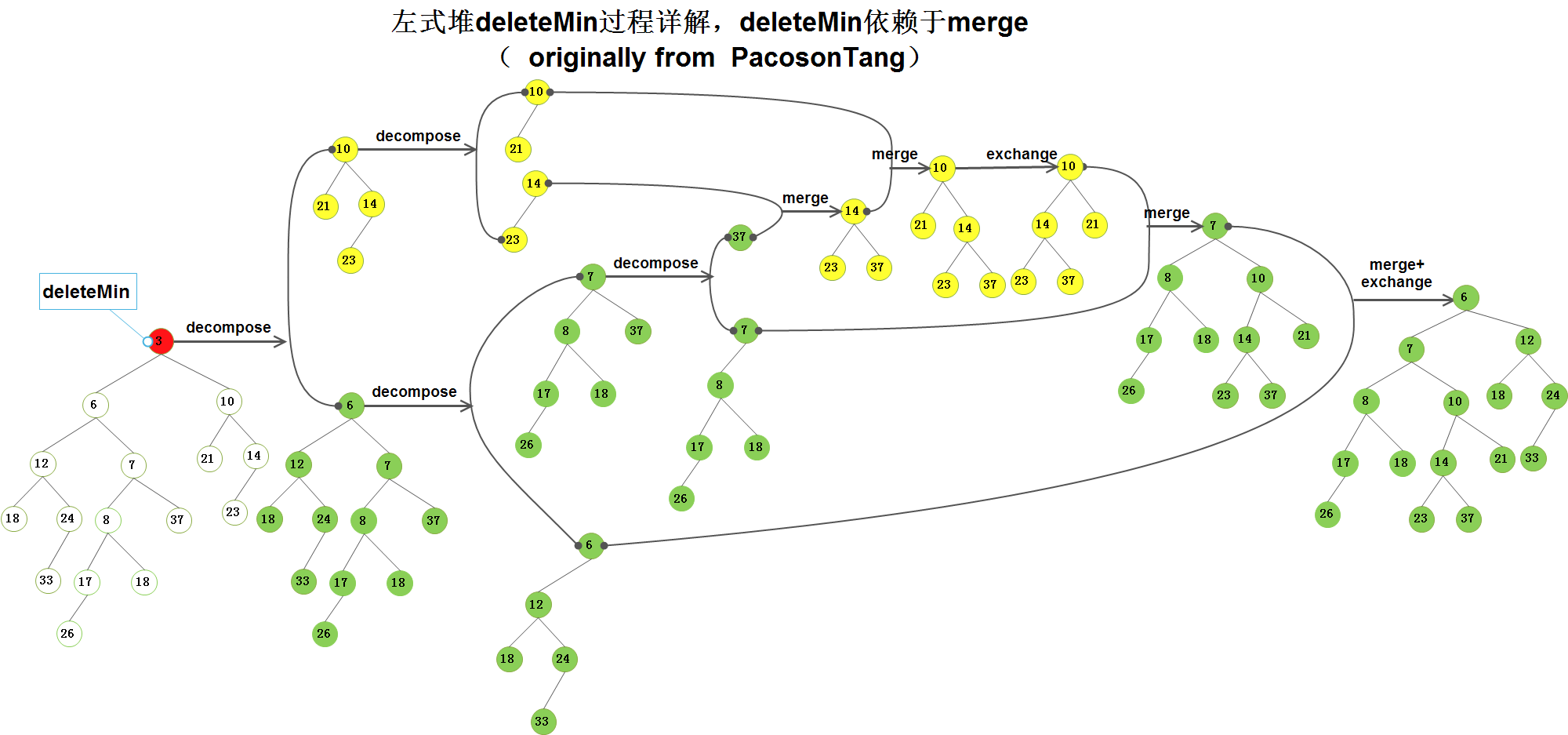
• A3）左式堆的核心操作是 merge， 无论insert 还是 deleteMin 都是基于 merge操作的；
• A4）左式堆的merge操作执行后，还要update 左式堆根节点的零路径长， 左式堆根节点的零路径长 == min{儿子的零路径长} +1；
• A5） update 后， 还需要比较 左右零路径长 是否满足左式堆的定义， 如果不满足，还需要交换左式堆根节点的左右孩子；

---

source code at a glance ）

#include "leftist_heap.h" 

// swap the left and the right in priority queue.
void swap(PriorityQueue h1)
{
    PriorityQueue temp;

    temp = h1->left;
    h1->left = h1->right;
    h1->right = temp;
}

// analog print directories and files name in the BinaryTree, which involves postorder traversal. 
void printPreorder(int depth, TreeNode root)
{           
    int i;

    if(root) 
    {      
        for(i = 0; i < depth; i++)
            printf("    ");     
        printf("%d
", root->value);
        printPreorder(depth + 1, root->left); 
         // Attention: there's difference between traversing binary tree and common tree.
        printPreorder(depth + 1, root->right);
    }
    else 
    {
        for(i = 0; i < depth; i++)
            printf("    ");     
        printf("NULL
");
    }
}

// insert an element with value into the priority queue.
PriorityQueue insert(ElementType value, PriorityQueue pq)
{
    TreeNode node;            

    node = (TreeNode)malloc(sizeof(struct TreeNode));
    if(!node)
    {
        Error("failed inserting, for out of space !");
        return pq;
    }
    node->left = NULL;
    node->right = NULL;
    node->nullPathLen = 0;
    node->value = value;    
    
    if(pq == NULL) // means that just only creating a node with value.
    {
        return node;
    }
    else
    {
        return merge(node, pq);        
    }
}

// return the minimal between a and b.
int minimal(int a, int b)
{
    return a > b ? b : a;
}

// merge the priority queue h1 and h2.
PriorityQueue merge(PriorityQueue h1, PriorityQueue h2)
{        
    if(h1 == NULL)
    {
        return h2;
    }
    else if(h2 == NULL)
    {
        return h1;
    }    
    if(h1->value > h2->value)
    {
        return innerMerge(h2, h1);
    }
    else
    {
        return innerMerge(h1, h2);
    }    
}

// merge the priority queue h1 and h2.
PriorityQueue innerMerge(PriorityQueue h1, PriorityQueue h2)
{ 
    if(h1->left == NULL)
    {
        h1->left = h2;
    }
    else
    {
        h1->right = merge(h1->right, h2);
        
    }    
    // update the null path length
    if(h1->right == NULL)
    {
        h1->nullPathLen = 0;
    }
    else
    {
        h1->nullPathLen = minimal(h1->left->nullPathLen, h1->right->nullPathLen) + 1;    
        // exchange the left and the right
        if(h1->left->nullPathLen < h1->right->nullPathLen)
        {
            swap(h1);
        }
    }
    return h1;
}

// delete the minimal element in the priority queue.
PriorityQueue deleteMin(PriorityQueue h1)
{
    PriorityQueue left;
    PriorityQueue right;

    if(!h1)
    {
        Error("failed deleteMin, for the root doesn't point to any position!");
        return NULL;
    }
    left = h1->left;
    right = h1->right;
    free(h1);

    return merge(left, right);
}

int main()
{
    PriorityQueue h1;
    PriorityQueue h2;    
    int data[] =  {21, 10, 23, 14, 3, 26, 17, 8};    
    int data2[] = {18, 12, 33, 24, 6, 37, 7, 18};    
    int i;

    h1 = insert(data[0], NULL);
    for(i=1; i<8; i++)
    {
        h1 = insert(data[i], h1);
    }
    printf("
=== after the leftist heap h1 is merged===
");
    printPreorder(1, h1);

    h2 = insert(data2[0], NULL);
    for(i=1; i<8; i++)
    {
        h2 = insert(data2[i], h2);
    }
    printf("
=== after the leftist heap h2 is merged===
");
    printPreorder(1, h2);
     
    h1 = merge(h1, h2);
    printf("
=== after both h1 and h2 are merged===
");
    printPreorder(1, h1);

    h1 = deleteMin(h1);
    printf("
=== after executing deleteMin operation ===
");
    printPreorder(1, h1);

    return  0;
}

---

printing results are as follows） 

Attention for analog between results and the 2 images above.