可以是空树。
性质:
任何父节点的左右子树深度差<=1;
BF平衡因子=左子树深度-右子树深度,则所有节点平衡因子-1,0,1;
有些BST初始序列或者插入后对BST的影响,导致可能出现下面这种情况,将导致我们的二叉排序树的效率大大降低:
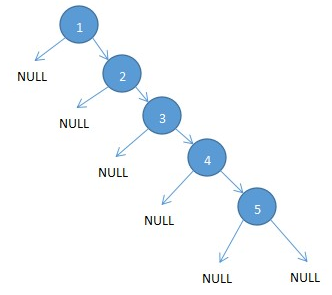
为了避免这种情况的发生,我们希望可以有一种算法,将我们的不平衡的二叉排序树转化为平衡二叉排序树。这样就可以让我们的二叉排序树结构最优化。
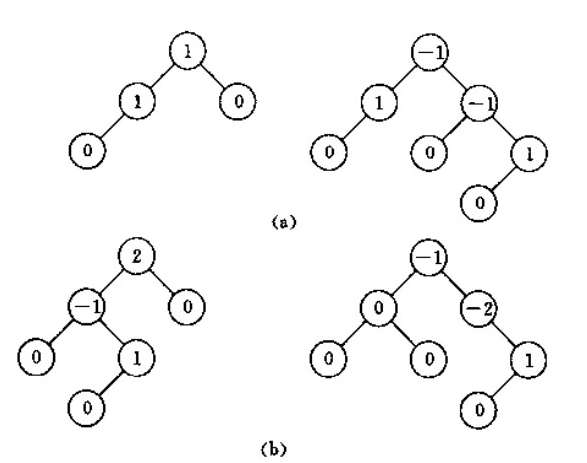
上图中a是,b不是。
为什么需要平衡二叉树?
平衡二叉树上的任何一个结点左右字数的深度之差都不会超过1,则可以证明它的深度和logn是同数量级的,所以其平均查找长度也和logn同数量级。
但是事于愿违有些二叉排序树的插入,或者初始序列由于其插入的先后顺序等缘故,将导致我们的二叉排序树的效率大大降低。如下图 :
为了避免这种情况的发生,我们希望可以有一种算法,将我们的不平衡的二叉排序树转化为平衡二叉排序树。这样就可以让我们的二叉排序树结构最优化。

a是AVL;
b也是;
c也是;
d不是,平衡因子出现了-2,将-2逆时针旋转(单向左旋平衡处理)得到e;
e是;
f不是,先将53顺时针旋转变成g,再将53逆时针旋转得到h;(双向旋转(先右后左)平衡处理)
如何证明我们插入的正确性:中序遍历所得关键字的值序列从小到大即可(二叉排序树的性质)
那么如何创建一颗平衡二叉树呢?
创建平衡二叉树,我们采用依次插入节点e的方式进行。
而平衡二叉树上插入节点采用递归的方式进行。
1、若空树,将e作为根节点,高度+1;
2、若要e==根节点,不插入;
3、e<root && 左子树种≠e,插入到左子树中,深度+1;
- 若root平衡因子-1,左浅右深,root左旋,root平衡因子变为0,BBST深度不变;
- root平衡因子0,root平衡因子改为1,BST深度+1;
- root平衡因子1,左深右浅。
- 若左子节点平衡因子1,右旋,根节点和其右子树根节点的平衡因子更改为0,树的深度不变;
- 若左子节点平衡因子-1,先左旋,后右旋,修改根节点和其左,右子树根节点的平衡因子,树的深度不变;
4、e>root && 右子树中≠e,插入到右子树中,深度+1;
- 若root平衡因子1,左深右浅,右旋,root改为0,深度不变;
- 若root平衡因子0,将root改为-1,不用旋,树深度+1;
- 若root平衡因子-1,左浅
(4)若e的关键字大于BBST的根节点的关键字,而且在BBST的右子树中不存在和e有相同关键字的节点,则将e插入到BBST的右子树上,并且当插入之后的右子树深度加1时,分别就不同的情况处理之。
-
BBST的根节点的平衡因子是1(左子树的深度大于右子树的深度):则将根节点的平衡因子修改为0(右旋),BBST的深度不变;
-
BBST的根节点的平衡因子是0(左右子树的深度相等):则将根节点的平衡因子修改为-1(不用旋),树的深度加1;
- BBST的根节点的平衡因子为-1(右子树的深度大于左子树的深度):若BBST的右子树根节点的平衡因子为1,则需要进行两次选择,第一次先向右旋转,再向左旋转处理,并且在旋转处理之后,修改根节点和其左,右子树根节点的平衡因子,树的深度不变;
若BBST的右子树根节点的平衡因子为1,则需要进行一次单向左的旋转处理,并且在左旋之后,更新根节点和其左,右子树根节点的平衡因子,树的深度不变;