【4】算法排序 （2路插入排序）

用二分查找法在有序表中找到正确的插入位置，是在折半插入排序的基础上改进，目的是减少排序过程中的移动次数；

基本思想:

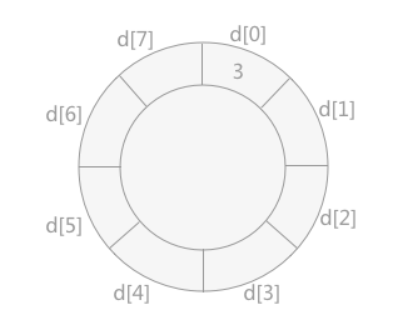
　　（1）另外设置一个同存储记录的数组大小相同的数组 d，将无序表中第一个记录添加进 d[0] 的位置上，然后从无序表中第二个记录开始，同 d[0] 作比较：如果该值比 d[0] 大，则添加到其右侧；反之添加到其左侧。

      （2）d可以理解为环形数组

　　（3）2-路插入排序相比于折半插入排序，只是减少了移动记录的次数，没有根本上避免，所以其时间复杂度仍为O(n2)。

     

  

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

void TwoWayInsert(int * a, int * t, int n)
{
        int i, min, max, k;
        // 分别记录t数组中 最大值和最小值的位置
        min = max = 0;

        // 初始化数组t
        t[0] = a[0];

        // a[i]:待插入的元素
        for (i=1; i<n; i++) {
                // 待插入的元素比最小元素小
                if (a[i] < t[min]) {
                        // 最大值的左边=最小值 环形
                        min = (min - 1 + n) % n;
                        t[min] = a[i];
                }
                // 待插入的元素比最大元素大
                else if (a[i] > t[max]) {
                        max = (max + 1 + n) % n;
                        t[max] = a[i];
                }
                // 待插入的元素在中间，比最小大，比最大小
                else {
                        k = (max + 1 + n) % n;
                        while(t[(k - 1 + n) % n] > a[i]) {
                                t[(k + n) % n] = t[(k - 1 + n) % n];
                                k = (k - 1 + n) % n;
                        }
                        // 插入该值
                        t[(k+n)%n] = a[i];
                        max = (max + 1 + n) % n;
                }
        }

        // 将排序记录复制到原来的顺序表里
        for (k=0; k<n; k++) {
                a[k] = t[(min + k)%n];
        }
}

void main()
{
        int a[8] = {21,3,7,9,39,20,8,4};
        int t[8];
        TwoWayInsert(a, t, 8);
        int i;
        for(i=0; i<8; i++) {
                printf("%d
", a[i]);
        }
}

 

参考: http://c.biancheng.net/view/3441.html