不按24题的顺序,按我做题的顺序
1、飞行员配对方案问题
建个图,跑遍匈牙利,让飞行员给其对应的飞机连一条边
#include <bits/stdc++.h>
using namespace std;
const int maxn=10000+10;
int n,m,e,head[maxn],to[maxn<<1],nxt[maxn<<1],vis[maxn],tot,ans,match[maxn];
inline void add(int x,int y){
to[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
int dfs(int x){
for(int i=head[x];i;i=nxt[i]){
int y=to[i];
if(!vis[y]){
vis[y]=1;
if(!match[y]||dfs(match[y])){
match[y]=x;return 1;
}
}
}
return 0;
}
int main()
{
scanf("%d%d",&n,&m);
int x,y;scanf("%d%d",&x,&y);
while(x!=-1&&y!=-1){
if(x<=n&&y<=n+m) add(x,y);
scanf("%d%d",&x,&y);
}
for(int i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
if(dfs(i)) ans++;
}
if(ans){
printf("%d
",ans);
for(int i=n+1;i<=m;i++)
if(match[i]) printf("%d %d
",match[i],i);
}
else printf("No Solution!
");
return 0;
}
2、试题库问题
相当于超级源连一条容量为试卷题目总数的边,每张试卷对题目连一条容量为(1)的边,题目对超级汇连一条容量为(1)的边
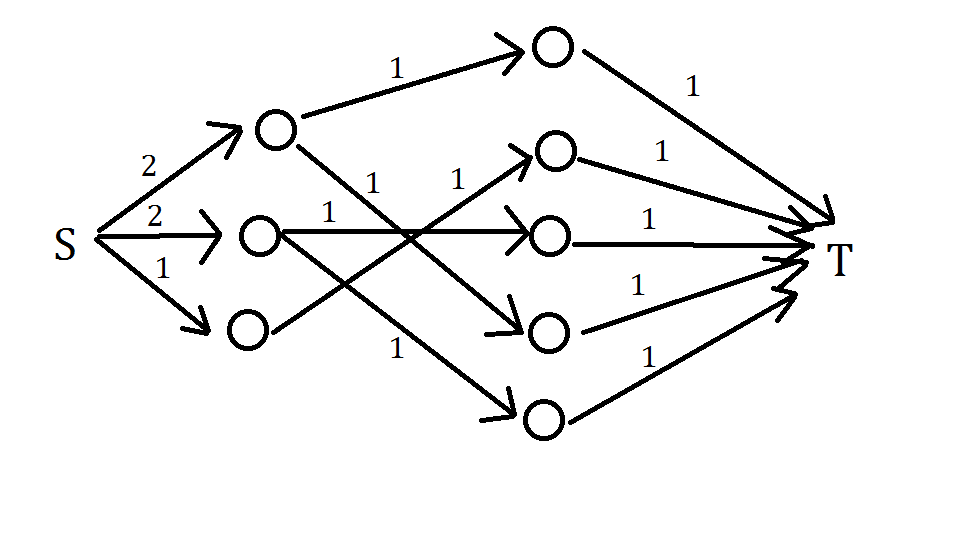
方案嘛就找一下残量网络中流量为(0)的正向边,然后输出一下它的朝向(e[i].to-k)
而且顺带说一句,每一张试卷的题目总数不一定等于它连出的边!
#include <bits/stdc++.h>
using namespace std;
const int maxn=100000+10;
const int inf=0x3f3f3f3f;
int k,n,m,s,t,head[maxn],tot=1;
int dep[maxn],cur[maxn];
struct node{
int to,next,val;
}e[maxn];
inline void add(int x,int y,int w){
e[++tot].to=y;
e[tot].val=w;
e[tot].next=head[x];
head[x]=tot;
}
int bfs(int s,int t){
queue<int> q;
for(int i=0;i<=t;i++)
cur[i]=head[i];
memset(dep,0x7f,sizeof(dep));
dep[s]=0;
q.push(s);
int u,v;
while(!q.empty()){
u=q.front(),q.pop();
for(int i=head[u];i;i=e[i].next){
v=e[i].to;
if(dep[v]>inf&&e[i].val){
dep[v]=dep[u]+1;
q.push(v);
}
}
}
return dep[t]<inf;
}
int dfs(int now,int t,int limit){
if(!limit||now==t) return limit;
int flow=0,f,v;
for(int i=cur[now];i;i=e[i].next){
cur[now]=i;v=e[i].to;
if(dep[v]==dep[now]+1&&(f=dfs(v,t,min(limit,e[i].val)))){
flow+=f;
limit-=f;
e[i].val-=f;
e[i^1].val+=f;
if(!limit) break;
}
}
return flow;
}
int Dinic(){
int maxflow=0;
while(bfs(s,t))
maxflow+=dfs(s,t,inf);
return maxflow;
}
int main()
{
scanf("%d%d",&k,&n);
s=0;t=n+k+1;
int x,y,w,p;
for(int i=1;i<=k;i++){
scanf("%d",&w);
add(s,i,w);add(i,s,0);
m+=w;
}
for(int i=1;i<=n;i++){
scanf("%d",&p);
for(int j=1;j<=p;j++){
scanf("%d",&x);
add(x,i+k,1);add(i+k,x,0);
}
}
for(int i=1;i<=n;i++){
add(i+k,t,1);add(t,i+k,0);
}
int maxflow=Dinic();
if(maxflow==m){
for(int x=1;x<=k;x++){
printf("%d:",x);
for(int i=head[x];i;i=e[i].next){
if(!e[i].val&&e[i].to>0){
printf("%d ",e[i].to-k);
}
}
printf("
");
}
}
else printf("No Solution
");
return 0;
}
3、最小路径覆盖问题
我用二分图做的,网络流我不知道。二分图建图好建,但是方案难输出
.
方案就是每次找到拆点的(i'),把它映射到(match[i]),开个(vis)数组存一下标记
#include <bits/stdc++.h>
using namespace std;
const int maxn=500+10;
int n,m,match[maxn],vis[maxn],ans;
vector<int> G[maxn];
int dfs(int x){
int y;
for(int i=0;i<G[x].size();i++){
y=G[x][i];
if(!vis[y]){
vis[y]=1;
if(!match[y]||dfs(match[y])){
match[y]=x;match[x]=y;
return 1;
}
}
}
return 0;
}
void print(int x){
x+=n;
for(int i=x;i;i=match[i-n]){
vis[i-n]=1;
printf("%d ",i-n);
}
printf("
");
}
int main()
{
scanf("%d%d",&n,&m);
int x,y;
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
G[x].push_back(y+n);
}
ans=n;
for(int i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
if(dfs(i)) ans--;
}
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++)
if(!vis[i]) print(i);
printf("%d
",ans);
return 0;
}
4、魔术球问题
这题贪心随便水,但是网络流可做
#include <bits/stdc++.h>
using namespace std;
const int maxn=100000+10;
const int inf=0x3f3f3f3f;
int n,m=5000,s=0,t=10000,head[maxn],tot=1,cnt;
int dep[maxn],cur[maxn],vis[maxn],nxt[maxn],ans[maxn];
struct node{
int to,next,val;
}e[maxn];
inline void add(int x,int y,int w){
e[++tot].to=y;
e[tot].val=w;
e[tot].next=head[x];
head[x]=tot;
}
int bfs(int s,int t){
queue<int> q;
for(int i=0;i<=t;i++)
cur[i]=head[i];
memset(dep,-1,sizeof(dep));
dep[s]=0;
q.push(s);
int u,v;
while(!q.empty()){
u=q.front(),q.pop();
for(int i=head[u];i;i=e[i].next){
v=e[i].to;
if(dep[v]==-1&&e[i].val){
dep[v]=dep[u]+1;
q.push(v);
}
}
}
return dep[t]!=-1;
}
int dfs(int now,int t,int limit){
if(!limit||now==t) return limit;
int flow=0,f,v;
for(int i=cur[now];i;i=e[i].next){
cur[now]=i;v=e[i].to;
if(dep[v]==dep[now]+1&&(f=dfs(v,t,min(limit,e[i].val)))){
flow+=f;
limit-=f;
e[i].val-=f;
e[i^1].val+=f;
if(!limit) break;
}
}
return flow;
}
int Dinic(){
int maxflow=0;
while(bfs(s,t))
maxflow+=dfs(s,t,inf);
return maxflow;
}
int main()
{
scanf("%d",&n);
int now=0,flow=0;
while(1){
flow++;now++;
for(int i=1;i<now;i++)
if(sqrt(i+now)==(int)sqrt(i+now)){
add(i,now+m,1);
add(now+m,i,0);
}
add(s,now,1);
add(now,s,0);
add(now+m,t,1);
add(t,now+m,0);
flow-=Dinic();
if(flow>n) break;
}
printf("%d
",--now);
for(int u=1;u<=now;u++){
for(int i=head[u];i;i=e[i].next){
if(!e[i].val){
nxt[u]=e[i].to-m;
break;
}
}
}
for(int i=1;i<=now;i++){
if(!vis[i]){
for(int u=i;u!=-m;u=nxt[u]){
vis[u]=1;
printf("%d ",u);
}
printf("
");
}
}
return 0;
}
5、方格取数问题
奇偶图弄一下,连容量为方格中的数,然后在相邻方格连一条容量为(inf)的边
#include <bits/stdc++.h>
using namespace std;
const int maxn=100000+10;
const int inf=1e9;
int n,m,s,t;
struct Edge{
int to,val,next;
}e[maxn<<1];
int head[maxn],cur[maxn],deep[maxn],tot=1;
int x[4]={0,0,1,-1},y[4]={1,-1,0,0};
void add(int x,int y,int w,int flag)
{
e[++tot].to=y;
e[tot].next=head[x];
head[x]=tot;
if(flag) e[tot].val=w;
}
int bfs(int s,int t)
{
queue<int> q;
for(int i=1;i<=n*m+2;i++)
cur[i]=head[i];
memset(deep,0x7f,sizeof(deep));
deep[s]=0;
q.push(s);
while(!q.empty())
{
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].next)
{
int y=e[i].to;
if(deep[y]>inf&&e[i].val)
{
deep[y]=deep[u]+1;
q.push(y);
}
}
}
if(deep[t]<inf)
return 1;
return 0;
}
int dfs(int now,int t,int limit)
{
if(!limit||now==t) return limit;
int f,flow=0;
for(int i=cur[now];i;i=e[i].next){
cur[now]=i;
if(deep[e[i].to]==deep[now]+1&&(f=dfs(e[i].to,t,min(limit,e[i].val)))){
flow+=f;
limit-=f;
e[i].val-=f;
e[i^1].val+=f;
if(!limit) break;
}
}
return flow;
}
int Dinic(){
int maxflow=0;
while(bfs(s,t))
maxflow+=dfs(s,t,inf);
return maxflow;
}
int main()
{
scanf("%d%d",&n,&m);s=n*m+1,t=n*m+2;
int sum=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
int x;scanf("%d",&x);sum+=x;
if((i+j)%2==1){add(s,(i-1)*m+j,x,1);add((i-1)*m+j,s,x,0);}
else {add((i-1)*m+j,t,x,1);add(t,(i-1)*m+j,x,0);}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
if((i+j)%2==1){
for(int k=0;k<4;k++){
int u=i+x[k],v=j+y[k];
if(u<1||u>n||v<1||v>m) continue;
add((i-1)*m+j,(u-1)*m+v,inf,1);
add((u-1)*m+v,(i-1)*m+j,inf,0);
}
}
}
printf("%d
",sum-Dinic());
return 0;
}
6、圆桌问题
比较经典的建图,类似试题库问题,经常结合二分答案+最大流判定(此题不用)
// luogu-judger-enable-o2
#include <bits/stdc++.h>
using namespace std;
const int maxn=100000+10;
const int inf=1e9;
int n,m,s,t;
struct Edge{
int to,val,next;
}e[maxn<<1];
int head[maxn],cur[maxn],deep[maxn],tot=1;
void add(int x,int y,int w,int flag)
{
e[++tot].to=y;
e[tot].next=head[x];
head[x]=tot;
if(flag) e[tot].val=w;
}
int bfs(int s,int t)
{
queue<int> q;
for(int i=0;i<=n+m+1;i++)
cur[i]=head[i];
memset(deep,0x7f,sizeof(deep));
deep[s]=0;
q.push(s);
while(!q.empty())
{
int u=q.front();q.pop();
for(int i=head[u];i;i=e[i].next)
{
int y=e[i].to;
if(deep[y]>inf&&e[i].val)
{
deep[y]=deep[u]+1;
q.push(y);
}
}
}
if(deep[t]<inf)
return 1;
return 0;
}
int dfs(int now,int t,int limit)
{
if(!limit||now==t) return limit;
int f,flow=0;
for(int i=cur[now];i;i=e[i].next){
cur[now]=i;
if(deep[e[i].to]==deep[now]+1&&(f=dfs(e[i].to,t,min(limit,e[i].val)))){
flow+=f;
limit-=f;
e[i].val-=f;
e[i^1].val+=f;
if(!limit) break;
}
}
return flow;
}
int Dinic(){
int maxflow=0;
while(bfs(s,t))
maxflow+=dfs(s,t,inf);
return maxflow;
}
int main()
{
scanf("%d%d",&n,&m);
s=0,t=n+m+1;
int x,sum=0;
for(int i=1;i<=n;i++){
scanf("%d",&x);
add(s,i,x,1);
add(i,s,x,0);
sum+=x;
}
for(int i=1;i<=m;i++){
scanf("%d",&x);
add(i+n,t,x,1);
add(t,i+n,x,0);
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
add(i,j+n,1,1);
add(j+n,i,1,0);
}
if(Dinic()==sum){
printf("1
");
for(int i=1;i<=n;i++){
for(int j=head[i];j;j=e[j].next)
if(e[j].to>n&&e[j].to<=n+m&&!e[j].val)
printf("%d ",e[j].to-n);
printf("
");
}
}
else printf("0
");
return 0;
}
8、孤岛营救问题
看到题解全是状压+(bfs),我也忍不住打了一个状压+(bfs),一遍过此题
#include <bits/stdc++.h>
using namespace std;
int n,m,p,k,s;
int vis[11][11][1<<11];
int mp[11][11][11][11];
int now[11][11],nx[4]={1,-1,0,0},ny[4]={0,0,1,-1};
struct point{
int x,y,sta,step;
};
int bfs(){
queue<point> q;
vis[0][0][0]=1;
q.push((point){1,1,0,0});
point u;int x,y,k;
while(!q.empty()){
u=q.front(),q.pop();
if(u.x==n&&u.y==m) return u.step;
for(k=0;k<4;k++){
x=u.x+nx[k];y=u.y+ny[k];
if(x<1||x>n||y<1||y>m||vis[x][y][u.sta|now[x][y]]) continue;
if(mp[u.x][u.y][x][y]==-1) continue;
if(mp[u.x][u.y][x][y]>0&&!(u.sta&(1<<mp[u.x][u.y][x][y]))) continue;
vis[x][y][u.sta|now[x][y]]=1;
q.push((point){x,y,u.sta|now[x][y],u.step+1});
}
}
return -1;
}
int main()
{
scanf("%d%d%d",&n,&m,&p);
scanf("%d",&k);
int x1,y1,x2,y2,g,x,y,q;
for(int i=0;i<k;i++){
scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&g);
if(!g) mp[x1][y1][x2][y2]=mp[x2][y2][x1][y1]=-1;
else mp[x1][y1][x2][y2]=mp[x2][y2][x1][y1]=g;
}
scanf("%d",&s);
for(int i=0;i<s;i++){
scanf("%d%d%d",&x,&y,&q);
now[x][y]|=1<<q;
}
printf("%d
",bfs());
return 0;
}
9、分配问题
二分图最佳完美匹配,可以类似网络流跑二分图跑两遍费用流,容量全部为(1),涉及超级源超级汇费用为(0),其他情况费用为(c_{ij})
#include <bits/stdc++.h>
using namespace std;
const int maxn=1000+10;
const int maxm=20000+10;
const int inf=0x3f3f3f3f;
int n,s,t,a[maxn][maxn],head[maxn],tot=1,maxflow,mincost;
int pre[maxn],last[maxn],flow[maxn],dis[maxn],vis[maxn];
struct node{
int to,next,flow,val;
}e[maxm];
inline void add(int x,int y,int w,int f){
e[++tot].to=y;
e[tot].flow=w;
e[tot].val=f;
e[tot].next=head[x];
head[x]=tot;
}
int spfa(){
memset(dis,inf,sizeof(dis));
memset(flow,inf,sizeof(flow));
memset(vis,0,sizeof(vis));
queue<int> q;
q.push(s);dis[s]=0;vis[s]=1;pre[t]=-1;
int u,v;
while(!q.empty()){
u=q.front(),q.pop();vis[u]=0;
for(int i=head[u];i;i=e[i].next){
v=e[i].to;
if(e[i].flow&&dis[v]>dis[u]+e[i].val){
dis[v]=dis[u]+e[i].val;
flow[v]=min(flow[u],e[i].flow);
pre[v]=u;last[v]=i;
if(!vis[v]){
vis[v]=1;
q.push(v);
}
}
}
}
return pre[t]!=-1;
}
void mcmf(){
int now;
while(spfa()){
now=t;
maxflow+=flow[t];
mincost+=flow[t]*dis[t];
while(now!=s){
e[last[now]].flow-=flow[t];
e[last[now]^1].flow+=flow[t];
now=pre[now];
}
}
}
int main()
{
scanf("%d",&n);
int f;s=0;t=n<<1|1;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++) scanf("%d",&a[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
add(i,j+n,1,a[i][j]);add(j+n,i,0,-a[i][j]);
}
for(int i=1;i<=n;i++){
add(s,i,1,0);add(i,s,0,0);
add(i+n,t,1,0);add(t,i+n,0,0);
}
mcmf();
printf("%d
",mincost);
tot=1;memset(head,0,sizeof(head));
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
add(i,j+n,1,-a[i][j]);add(j+n,i,0,a[i][j]);
}
for(int i=1;i<=n;i++){
add(s,i,1,0);add(i,s,0,0);
add(i+n,t,1,0);add(t,i+n,0,0);
}
maxflow=mincost=0;
mcmf();
printf("%d
",-mincost);
return 0;
}
10、运输问题
此题是上题的加强版,其他都一样,就是涉及超级源和超级汇的容量是输入的(a_i)和(b_j),因为(sum_{i=1}^{m}a_i=sum_{j=1}^{n}b_j),所以就是求满流的情况下的最小费用和最大费用,跑两遍费用流
最后就是最大费用边连成负边,最后(-mincost)就是最大费用
#include <bits/stdc++.h>
using namespace std;
const int maxn=200+10;
const int maxm=30000+10;
const int inf=0x3f3f3f3f;
int n,m,s,t,a[maxn],b[maxn],c[maxn][maxn],head[maxn],tot=1,maxflow,mincost;
int dis[maxn],vis[maxn],flow[maxn],pre[maxn],last[maxn];
struct node{
int to,next,flow,val;
}e[maxm];
inline int read(){
register int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return (f==1)?x:-x;
}
inline void add(int x,int y,int w,int f){
e[++tot].to=y;
e[tot].flow=w;
e[tot].val=f;
e[tot].next=head[x];
head[x]=tot;
}
int spfa(){
memset(dis,inf,sizeof(dis));
memset(flow,inf,sizeof(flow));
memset(vis,0,sizeof(vis));
queue<int> q;
q.push(s);dis[s]=0;vis[s]=1;pre[t]=-1;
int u,v;
while(!q.empty()){
u=q.front(),q.pop();vis[u]=0;
for(int i=head[u];i;i=e[i].next){
v=e[i].to;
if(e[i].flow>0&&dis[v]>dis[u]+e[i].val){
dis[v]=dis[u]+e[i].val;
flow[v]=min(flow[u],e[i].flow);
pre[v]=u;last[v]=i;
if(!vis[v]){
vis[v]=1;
q.push(v);
}
}
}
}
return pre[t]!=-1;
}
void mcmf(){
int now;
while(spfa()){
now=t;
maxflow+=flow[t];
mincost+=flow[t]*dis[t];
while(now!=s){
e[last[now]].flow-=flow[t];
e[last[now]^1].flow+=flow[t];
now=pre[now];
}
}
}
int main()
{
n=read(),m=read();
s=0,t=n+m+1;
int f;
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<=m;i++) b[i]=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) c[i][j]=read();
for(int i=1;i<=n;i++) add(s,i,a[i],0),add(i,s,0,0);
for(int i=1;i<=m;i++) add(i+n,t,b[i],0),add(t,i+n,0,0);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) add(i,j+n,inf,c[i][j]),add(j+n,i,0,-c[i][j]);
mcmf();
printf("%d
",mincost);
tot=1;memset(head,0,sizeof(head));
for(int i=1;i<=n;i++) add(s,i,a[i],0),add(i,s,0,0);
for(int i=1;i<=m;i++) add(i+n,t,b[i],0),add(t,i+n,0,0);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) add(i,j+n,inf,-c[i][j]),add(j+n,i,0,c[i][j]);
maxflow=mincost=0;
mcmf();
printf("%d
",-mincost);
return 0;
}