面试题8：二叉树的下一个节点

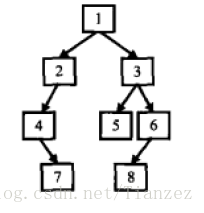
一.题目

给定一棵二叉树和其中的一个结点，如何找出中序遍历顺序的下一个结点？树中的结点除了有两个分别指向左右子结点的指针以外，还有一个指向父结点的指针。

二.思路

分析题目之后，我们发现，待处理节点只存在三种状态，我们分别处理即可：

1. 待处理节点有右子树。那么它的下一个节点为其右子树的最左子节点，如上图节点3的下一个节点为8；
2. 待处理节点无右子树，且是父节点的左节点。那么它的下一个节点为其父节点，如上图节点5的下一个节点为3；
3. 待处理节点无右子树，且是父节点的右节点。我们可以沿着它的父节点向上遍历，直至找到一个这样的节点，该节点是其父节点的左子节点，那么该节点的父节点就是所求节点，如上图节点6的下一个节点为1.

三.代码

BinaryTreeNode* GetNext(BinaryTreeNode* pNode){
    
    if(pNode == nullptr)
        return nullptr;

    BinaryTreeNode* pNext = nullptr;
    if(pNode->m_pRight != nullptr){
        BinaryTreeNode* pRight = pNode->m_pRight;
        while(pRight->m_pLeft != nullptr)
            pRight = pRight->m_pLeft;
        pNext = pRight;

    }

    else if(pNode->m_pParent != nullptr){
        BinaryTreeNode* pCurrent = pNode;
        BinaryTreeNode* pParent = pNode->m_pParetn;

        while(pParent != nullptr && pNode = pParent->m_pRight){
            pCurrent = pParent;
            pParent = pParent->m_pParent;
        }
        pNext = pParent;

    }
    return pNext;

}

四.本题考点

1. 考查应聘者对二叉树遍历的理解程度。只有对二叉树的遍历算法有了深刻的理解，应聘者才有可能准确找出每个节点的中序遍历的下一个节点。
2. 考查应聘者分析复杂问题的能力。应聘者只有画出二叉树的结构图、通过具体的例子找出中序遍历的下一个节点的规律，才有可能设计出可行的算法。