Kmp算法和BF算法的区别在于不需要把“搜索位置”移动到已经比较过的位置。
例子-->
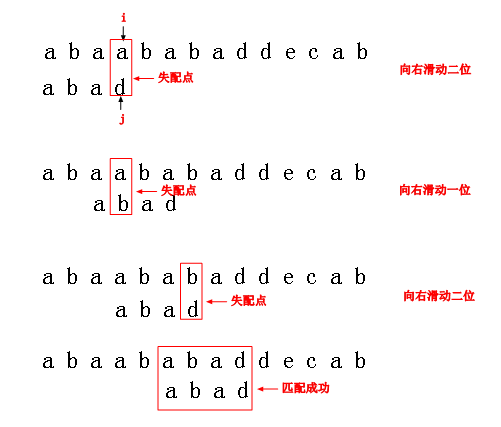
->移动位数 = 已经匹配的字符数 - 对应匹配部分字符串前缀和后缀共有长度
如以上主串中的“abab”和目标串中的“abad”,已经匹配的字符数为3(“aba”),
“aba”的前缀为[a,ab],后缀为[ba,a]。共有“a”的长度为1 ,移动位数=3-1=2;
因此目标串中的匹配字符串前缀和后缀信息是固定的,我现在只需要把这个信息放在一个数组里
->next数组的含义就是一个固定字符串的最长前缀和最长后缀相同的长度。
对于目标字符串ptr,ababaca,长度是7,所以next[0],next[1],next[2],next[3],next[4],next[5],next[6]分别计算的是
a,ab,aba,abab,ababa,ababac,ababaca的相同的最长前缀和最长后缀的长度。由于a,ab,aba,abab,ababa,ababac,ababaca的相同的最长前缀和最长后缀是“”,“”,“a”,“ab”,“aba”,“”,“a”,所以next数组的值是[-1,-1,0,1,2,-1,0],这里-1表示不存在,0表示存在长度为1,2表示存在长度为3。
求next数组c#代码-->
private static unsafe int[] cal_next(string str) { int len = str.Length; int[] next = new int[len]; next[0] = -1; int k = -1; for (int q=1;q< len;q++) { while(k>-1&&str[k+1]!=str[q]) { k = next[k]; } if (str[k+1] == str[q]) { k = k + 1; } next[q] = k; } return next; }
求匹配位置kmr c#代码-->
private static int kmr(string m,string s) { int m_len = m.Length; int s_len = s.Length; int[] next = cal_next(s); int k = -1; for(int i=0;i<m_len;i++) { while(k>-1 && s[k+1]!=m[i]) { k = next[k]; } if (s[k+1] == m[i]) { k = k + 1; } if(k==s_len-1) { return i - s_len + 1; } } return -1; }
参考-->
1-> http://blog.csdn.net/hyjoker/article/details/51190726
2-> https://www.cnblogs.com/huangxincheng/archive/2012/12/01/2796993.html