hdu 1198 Farm Irrigation

Problem Description

Benny has a spacious farm land to irrigate. The farm land is a rectangle, and is divided into a lot of samll squares. Water pipes are placed in these squares. Different square has a different type of pipe. There are 11 types of pipes, which is marked from A to K, as Figure 1 shows.


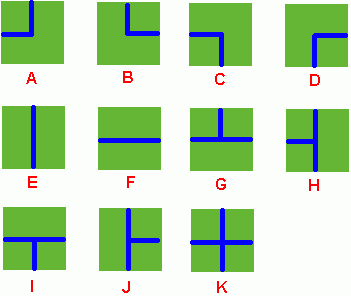
Figure 1

Benny has a map of his farm, which is an array of marks denoting the distribution of water pipes over the whole farm. For example, if he has a map 

ADC
FJK
IHE

then the water pipes are distributed like 


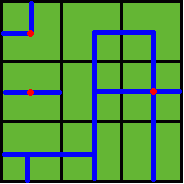
Figure 2

Several wellsprings are found in the center of some squares, so water can flow along the pipes from one square to another. If water flow crosses one square, the whole farm land in this square is irrigated and will have a good harvest in autumn. 

Now Benny wants to know at least how many wellsprings should be found to have the whole farm land irrigated. Can you help him? 

Note: In the above example, at least 3 wellsprings are needed, as those red points in Figure 2 show.

 

Input

There are several test cases! In each test case, the first line contains 2 integers M and N, then M lines follow. In each of these lines, there are N characters, in the range of 'A' to 'K', denoting the type of water pipe over the corresponding square. A negative M or N denotes the end of input, else you can assume 1 <= M, N <= 50.

 

Output

For each test case, output in one line the least number of wellsprings needed.

 

Sample Input

2 2

DK

HF

3 3

ADC

FJK

IHE

-1 -1

 

Sample Output

2

3

 

http://acm.hdu.edu.cn/showproblem.php?pid=1198;

简单搜索题目；

题目思路：

1、首先把A——F的每一个形状描述出来（可以与另一个想通的赋值为1，无法相通的赋值为0，每一个方形都有四个值up,down,left,right);

2、判断与下一个方形是否会相通，根据相对位置，如果本身在下一个方形的上面，则判断本身的down与下一个方形的up值是不是都是1，是的话，就能相通，则标记次方形。

其他的相对位置同理去思考，不作具体解释。。。

#include <iostream>
#include <stdio.h>
#include <queue>
#include <string.h>
using namespace std;
struct node
{
    int up,down,left,right;
}dd[11];

int dir[][2]={{1,0},{0,1},{-1,0},{0,-1}};

struct node2
{
    int xx,yy;
};

int m,n;
int map[55][55];
bool flag[55][55];
queue<node2>q;

bool judge(node2 p,node2 temp,int kk)
{
    if(kk==0)//上下;
    {
        if(dd[map[p.xx][p.yy]].down==1 && dd[map[temp.xx][temp.yy]].up==1)
        {
            return true;
        }
        else
        {
            return false;
        }
    }
    else if(kk==1)//左右；
    {
        if(dd[map[p.xx][p.yy]].right==1 && dd[map[temp.xx][temp.yy]].left==1)
        {
            return true;
        }
        else
        {
            return false;
        }
    }
    else if(kk==2)//下上；
    {
        if(dd[map[p.xx][p.yy]].up==1 && dd[map[temp.xx][temp.yy]].down==1)
        {
            return true;
        }
        else
        {
            return false;
        }
    }
    else   //右左;
    {
        if(dd[map[p.xx][p.yy]].left==1 && dd[map[temp.xx][temp.yy]].right==1)
        {
            return true;
        }
        else
        {
            return false;
        }
    }
}

bool judge2(node2 temp)
{
    if(temp.xx<0 || temp.xx>=m || temp.yy<0 || temp.yy>=n || flag[temp.xx][temp.yy])
    return false;
    return true;
}

void bfs(int x,int y)
{
    while(!q.empty())
    {
        q.pop();
    }
    node2 temp,p;
    int i;
    p.xx=x;
    p.yy=y;
    q.push(p);
    flag[x][y]=true;
    while(!q.empty())
    {
        p=q.front();
        q.pop();
        for(i=0;i<4;i++)
        {
            temp=p;
            temp.xx+=dir[i][0];
            temp.yy+=dir[i][1];
            if(!judge2(temp))
            continue;
            if(judge(p,temp,i))
            {
                q.push(temp);
                flag[temp.xx][temp.yy]=true;
            }
        }
    }

}
void init()
{
    dd[0].up=1,dd[0].down=0,dd[0].left=1,dd[0].right=0;
    dd[1].up=1,dd[1].down=0,dd[1].left=0,dd[1].right=1;
    dd[2].up=0,dd[2].down=1,dd[2].left=1,dd[2].right=0;
    dd[3].up=0,dd[3].down=1,dd[3].left=0,dd[3].right=1;
    dd[4].up=1,dd[4].down=1,dd[4].left=0,dd[4].right=0;
    dd[5].up=0,dd[5].down=0,dd[5].left=1,dd[5].right=1;
    dd[6].up=1,dd[6].down=0,dd[6].left=1,dd[6].right=1;
    dd[7].up=1,dd[7].down=1,dd[7].left=1,dd[7].right=0;
    dd[8].up=0,dd[8].down=1,dd[8].left=1,dd[8].right=1;
    dd[9].up=1,dd[9].down=1,dd[9].left=0,dd[9].right=1;
    dd[10].up=1,dd[10].down=1,dd[10].left=1,dd[10].right=1;
    memset(flag,false,sizeof(flag));

}
int main()
{
    while(~scanf("%d%d",&m,&n))
    {
        int i,j;
        if(m<0 || n<0)
        break;
        init();
        char op;
        for(i=0;i<m;i++)
        {
            for(j=0;j<n;j++)
            {
                cin>>op;
                map[i][j]=op-'A';
            }
        }

        int cnt=0;

        for(i=0;i<m;i++)
        {
            for(j=0;j<n;j++)
            {
                if(!flag[i][j])
                {
                    bfs(i,j);
                    cnt++;
                }
            }
        }
        printf("%d\n",cnt);

    }
    return 0;
}