突破蝙蝠的包围,yifenfei来到一处悬崖面前,悬崖彼岸就是前进的方向,好在现在的yifenfei已经学过御剑术,可御剑轻松飞过悬崖。
现在的问题是:悬崖中间飞着很多红,黄,蓝三种颜色的珠子,假设我们把悬崖看成一条长度为n的线段,线段上的每一单位长度空间都可能飞过红,黄,蓝三种珠子,而yifenfei必定会在该空间上碰到一种颜色的珠子。如果在连续3段单位空间碰到的珠子颜色都不一样,则yifenfei就会坠落。
比如经过长度为3的悬崖,碰到的珠子先后为 “红黄蓝”,或者 “蓝红黄” 等类似情况就会坠落,而如果是 “红黄红” 或者 “红黄黄”等情况则可以安全到达。
现在请问:yifenfei安然抵达彼岸的方法有多少种?

现在的问题是:悬崖中间飞着很多红,黄,蓝三种颜色的珠子,假设我们把悬崖看成一条长度为n的线段,线段上的每一单位长度空间都可能飞过红,黄,蓝三种珠子,而yifenfei必定会在该空间上碰到一种颜色的珠子。如果在连续3段单位空间碰到的珠子颜色都不一样,则yifenfei就会坠落。
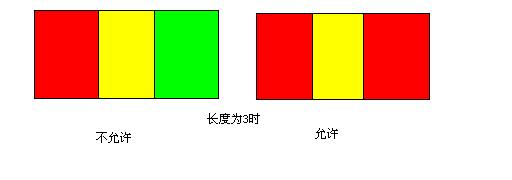
比如经过长度为3的悬崖,碰到的珠子先后为 “红黄蓝”,或者 “蓝红黄” 等类似情况就会坠落,而如果是 “红黄红” 或者 “红黄黄”等情况则可以安全到达。
现在请问:yifenfei安然抵达彼岸的方法有多少种?


Input
输入数据首先给出一个整数C,表示测试组数。
然后是C组数据,每组包含一个正整数n (n<40)。
然后是C组数据,每组包含一个正整数n (n<40)。
Output
对应每组输入数据,请输出一个整数,表示yifenfei安然抵达彼岸的方法数。
每组输出占一行。
每组输出占一行。
Sample Input
2 2 3
Sample Output
9 21
 View Code
View Code
1 #include<iostream> 2 #include<stdio.h> 3 #include<string.h> 4 using namespace std; 5 int main() 6 { 7 int t; 8 scanf("%d",&t); 9 while(t--) 10 { 11 int n; 12 scanf("%d",&n); 13 __int64 dd1,dd2,dd3,dd; 14 dd1=3; 15 dd2=9; 16 dd3=21; 17 if(n==1) 18 { 19 printf("%I64d\n",dd1); 20 continue; 21 } 22 else if(n==2) 23 { 24 printf("%I64d\n",dd2); 25 continue; 26 } 27 else if(n==3) 28 { 29 printf("%I64d\n",dd3); 30 continue; 31 } 32 else 33 { 34 int i; 35 for(i=4;i<=n;i++) 36 { 37 dd=2*dd3+dd2; 38 dd2=dd3; 39 dd3=dd; 40 } 41 printf("%I64d\n",dd); 42 } 43 } 44 return 0; 45 }
找规律,首先当n=1时,结果是3;
n=2时,结果是9;
n=3时,结果是21;
n=4时,结果是51;
因此,不难发现,D(n)=D(n-1)*2+D(n-2);
详细看代码。
