首先要先清楚最大流的含义,就是说从源点到经过的所有路径的最终到达汇点的所有流量和EK算法的核心
反复寻找源点s到汇点t之间的增广路径,若有,找出增广路径上每一段[容量-流量]的最小值delta,若无,则结束。
在寻找增广路径时,可以用BFS来找,并且更新残留网络的值(涉及到反向边)。
而找到delta后,则使最大流值加上delta,更新为当前的最大流值。
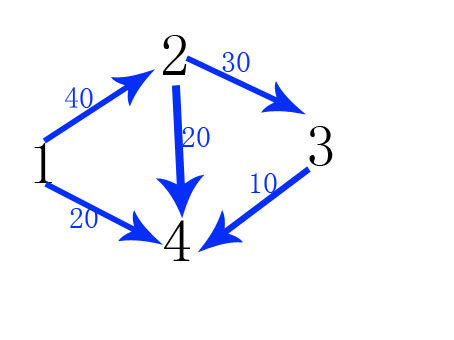
这么一个图,求源点1,到汇点4的最大流
由于我是通过模版真正理解ek的含义,所以先上代码,通过分析代码,来详细叙述ek算法

1 #include <iostream> 2 #include <queue> 3 #include<string.h> 4 using namespace std; 5 #define arraysize 201 6 int maxData = 0x7fffffff; 7 int capacity[arraysize][arraysize]; //记录残留网络的容量 8 int flow[arraysize]; //标记从源点到当前节点实际还剩多少流量可用 9 int pre[arraysize]; //标记在这条路径上当前节点的前驱,同时标记该节点是否在队列中 10 int n,m; 11 queue<int> myqueue; 12 int BFS(int src,int des) 13 { 14 int i,j; 15 while(!myqueue.empty()) //队列清空 16 myqueue.pop(); 17 for(i=1;i<m+1;++i) 18 { 19 pre[i]=-1; 20 } 21 pre[src]=0; 22 flow[src]= maxData; 23 myqueue.push(src); 24 while(!myqueue.empty()) 25 { 26 int index = myqueue.front(); 27 myqueue.pop(); 28 if(index == des) //找到了增广路径 29 break; 30 for(i=1;i<m+1;++i) 31 { 32 if(i!=src && capacity[index][i]>0 && pre[i]==-1) 33 { 34 pre[i] = index; //记录前驱 35 flow[i] = min(capacity[index][i],flow[index]); //关键:迭代的找到增量 36 myqueue.push(i); 37 } 38 } 39 } 40 if(pre[des]==-1) //残留图中不再存在增广路径 41 return -1; 42 else 43 return flow[des]; 44 } 45 int maxFlow(int src,int des) 46 { 47 int increasement= 0; 48 int sumflow = 0; 49 while((increasement=BFS(src,des))!=-1) 50 { 51 int k = des; //利用前驱寻找路径 52 while(k!=src) 53 { 54 int last = pre[k]; 55 capacity[last][k] -= increasement; //改变正向边的容量 56 capacity[k][last] += increasement; //改变反向边的容量 57 k = last; 58 } 59 sumflow += increasement; 60 } 61 return sumflow; 62 } 63 int main() 64 { 65 int i,j; 66 int start,end,ci; 67 while(cin>>n>>m) 68 { 69 memset(capacity,0,sizeof(capacity)); 70 memset(flow,0,sizeof(flow)); 71 for(i=0;i<n;++i) 72 { 73 cin>>start>>end>>ci; 74 if(start == end) //考虑起点终点相同的情况 75 continue; 76 capacity[start][end] +=ci; //此处注意可能出现多条同一起点终点的情况 77 } 78 cout<<maxFlow(1,m)<<endl; 79 } 80 return 0; 81 }
显而易见capacity存变的流量,进行ek求解
对于BFS找增广路:
1. flow[1]=INF,pre[1]=0;
源点1进队列,开始找增广路,capacity[1][2]=40>0,则flow[2]=min(flow[1],40)=40;
capacity[1][4]=20>0,则flow[4]=min(flow[1],20)=20;
capacity[2][3]=30>0,则flow[3]=min(folw[2]=40,30)=30;
capacity[2][4]=30,但是pre[4]=1(已经在capacity[1][4]这遍历过4号点了)
capacity[3][4].....
当index=4(汇点),结束增广路的寻找
传递回increasement(该路径的流),利用前驱pre寻找路径,路径也自然变成了这样:

2.flow[1]=INF,pre[1]=0;
源点1进队列,开始找增广路,capacity[1][2]=40>0,则flow[2]=min(flow[1],40)=40;
capacity[1][4]=0!>0,跳过
capacity[2][3]=30>0,则flow[3]=min(folw[2]=40,30)=30;
capacity[2][4]=30,pre[4]=2,则flow[2][4]=min(flow[2]=40,20)=20;
capacity[3][4].....
当index=4(汇点),结束增广路的寻找
传递回increasement(该路径的流),利用前驱pre寻找路径,图也被改成

接下来同理
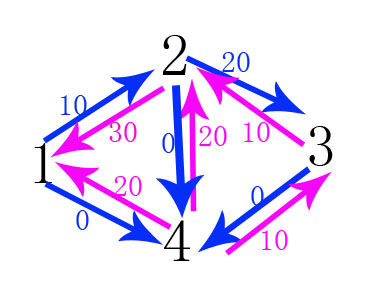
这就是最终完成的图,最终sumflow=20+20+10=50(这个就是最大流的值)
PS,为什么要有反向边呢?

我们第一次找到了1-2-3-4这条增广路,这条路上的delta值显然是1。于是我们修改后得到了下面这个流。(图中的数字是容量)

这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是1。
但这个答案明显不是最大流,因为我们可以同时走1-2-4和1-3-4,这样可以得到流量为2的流。
那么我们刚刚的算法问题在哪里呢?问题就在于我们没有给程序一个”后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢?回溯搜索吗?那么我们的效率就上升到指数级了。
而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边(I,j)都有一条反向边(j,i),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少delta的同时,也把每一段上的反方向的容量增加delta。即在Dec(c[x,y],delta)的同时,inc(c[y,x],delta)
我们来看刚才的例子,在找到1-2-3-4这条增广路之后,把容量修改成如下
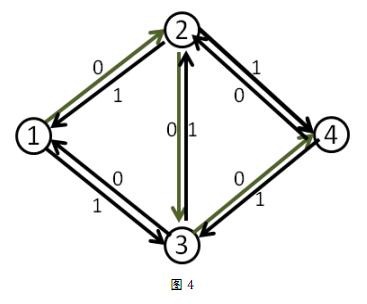
这时再找增广路的时候,就会找到1-3-2-4这条可增广量,即delta值为1的可增广路。将这条路增广之后,得到了最大流2。

那么,这么做为什么会是对的呢?我来通俗的解释一下吧。
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给”退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。(有人问如果这里没有2-4怎么办,这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流量。
这就是这个算法的精华部分,利用反向边,使程序有了一个后悔和改正的机会。而这个算法和我刚才给出的代码相比只多了一句话而已。
至此,最大流Edmond-Karp算法介绍完毕。
更复杂的最小值流问题 每条边不仅有容量 还有单位流的价值 求解所有最大流中最小价值的流。最大流和最小值流问题都是仍然在研究中。
转自:http://www.cnblogs.com/zsboy/archive/2013/01/27/2878810.html
