TransE 理解
一、输入:
实体集合E = {e1,e2,……,en},
关系集合 L = { l1 , l2 ,……, lm },
三元组 S { (ei1,ej1, lj1),……,(eim,ejm, ljm)}
Embeddings dim : k
Margin : 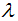
Learing Rate : LR
二、输出:
实体集合的向量表示:
E = {e1=(x1,x2,……,xk),e2=(x1,x2,……,xk),……,en=(x1,x2,……,xk)}
关系集合的向量表示
L = {l1=(x1,x2,……,xk),l2=(x1,x2,……,xk),……,ln=(x1,x2,……,xk)}
三、优化目标(取最小值):
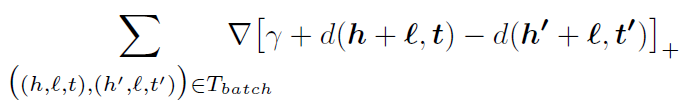
四、算法

五、算法理解
5.1 初始化关系集合L
li=( li: x1,x2,……,xk)
其中l中的每一个元素由公式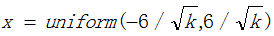 来计算,uniform(a,b)表示[a,b)之间的一个随机数
来计算,uniform(a,b)表示[a,b)之间的一个随机数
对l单位化
5.2 初始化实体集合E
初始化方式同初始化关系集合L
ei=( ei: x1,x2,……,xk)
5.3 在三元组S中随机选择一个子集Sbatch
令 Tbatch 等于空集
对每一个s=(h,l,t) ,生产 s’=(h’,l,t’) 其中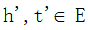 而且h’ != h, t’ != t
而且h’ != h, t’ != t
Tbatch = Tbatch + {((h,l,t),(h’,l,t’))}
更新优化目标:
按如下公式更新h,t,l,h’,t’
positive = 2 * LR * (t_before_batch - h_before_batch - l_before_batch)
negtative = 2 * LR * (t'_before_batch - h'_before_batch - l_before_batch)
h = h + positive
t = t - positive
l = l + positive - negtative
h' = h' - negtative
t' = t' + negtative
当优化目标取得最小值时,程序结束