朴素贝叶斯法

一、朴素贝叶斯法

　　　朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入输出的联合概率分布，然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。

二、数学理论

2.1 条件概率公式

　　P(X=x|Y=C_k)=P(Y=C_k , X=x)/P(X=x)

2.2 条件独立假设

　　

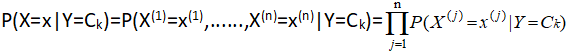
2.3 极大似然估计

　　

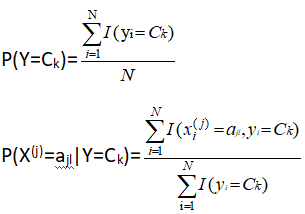
2.4 输出

 　　

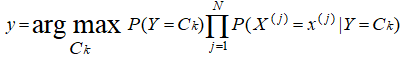
三、基本方法：

　　设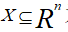为n维向量的集合，输出空间为标记集合Y={C₁,C₂,......,C_k}. P(X,Y)是定义在X和Y上的联合概率分布。

3.1条件概率分布：

　　P(X=x|Y=C_k)=P(X⁽¹⁾=x⁽¹⁾,......,X⁽ⁿ⁾=x⁽ⁿ⁾|Y=C_k). 朴素贝叶斯法对条件概率分布作了条件独立假设，故而

　　

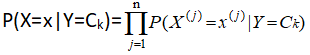
　　而P(Y=C_k|X=x)=P(Y=C_k,X=x)/P(X=x),要使得P(Y=C_k|X=x)最大，对于不同的类别，分母相同，只要使得分子最大。

而分子:

　　

3.2极大似然估

　　根据极大似然估计可求得P(Y=C_k)和P(X^(j)=x^(j)|Y=C_k)

　　

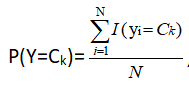
　　其中N为样本容量的个数。设第j个特征x^(j)可能取值的集合为{a_j1,a_j2,......,},则

　　

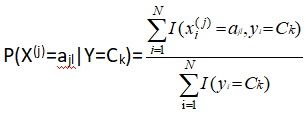
　　故而，当样本确定以后，

  

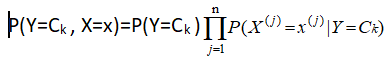
   可计算，从而可比较出最大值，从而确定X=x_i时Y的分类。