动态规划-带权区间问题

一、动态规划算法的定义：

　　为了着手开发一个动态规划算法，我们需要一组从初始问题导出的满足某些基本性质的子问题。

1. 只存在多项式个子问题
2. 可以容易的从子问题的解计算出初始问题的解
3. 在子问题中，从“最小”到“最大”存在一种自然的顺序，与一个容易计算的递推公式相联系。这个递推公式允许我们从某些更小的子问题的解来确定一个子问题的解。

二、带权区间调度问题：

　　我们有N个需求，标记为1,2,3,......,N,每个需求指定一个开始时间s_i,结束时间f_i ,每个需求i有一个权值v_i,如果两个需求不重叠，那么他们是相容的。

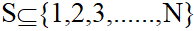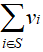　　目标：选择一个两两相容的子集，使得最大。

三、动态规划算法：

　　首先让所有的需求按照结束时间非降序排序:f₁<=f₂.....<f_n

　　定义p(j) 为使得区间i与j不相交的最大的标记，既i是最右边的在j开始之前的区间。

　　设最优解为O,则显然对每个区间都有：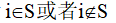

　　令区间{1,2,3,......,j}的最优解为OPT(j)

　　则：

　　　　OPT(j) = MAX( v_j + OPT(p(j)), OPT(j-1))

　　并且需求j属于OPT(j)，当且仅当：

　　　　OPT(p(j)) + v_j >= OPT(j-1)

 

动态规划算法如下：

1. 求出所有的OPT(j)

　　　 其中数组M用于存储OPT(j)

　　  M-Comupte-OPT(j)

　　　　 If j == 0 then

　　　　　　Return 0

　　　  Else if M[j] 不为空 then

　　　　　　Return M[j]

　　　  Else

　　　　　　M[j] = MAX( v_j + Comupte-OPT(p(j)), Comupte-OPT(j-1))

　　　　　　Return M[j]

　　　　 End

　　　　

　　2. 根据上一步求出的OPT[j]，求出最优解中包含的区间

　　　Find-Solution(j)

　　　　If j == 0 then

　　　　　　Return “”;

　　　　Else

　　　　　　If  OPT(p(j)) + v_j >= OPT(j-1) then

　　　　　　　　Return j + Find-Solution(p(j))

　　　　　　Else

　　　　　　　　Return Find-Solution(p(j))

        End

　　   End