-------------------------------------------------------------------------------------------
1,一根木棒,截成三截,组成三角形的概率是多少?
2,抛一个六面的色子,连续抛直到抛到6为止,问期望的抛的次数是多少?
3,一个木桶里面有M个白球,每分钟从桶中随机取出一个球涂成红色(无论白或红都涂红)再放回,问将桶中球全部涂红的期望时间是多少?
4,你有一把宝剑。每使用一个宝石,有50%的概率会成功让宝剑升一级,50%的概率会失败。如果宝剑的级数大于等于5的话,那么失败会使得宝剑降1级。如果宝剑的级数小于5的话,失败没有效果。问题是:期望用多少个宝石可以让一把1级的宝剑升到9级?
5,一个黑盒里是一个图,结构未知,只知道点的个数是n,边的个数是m,写公式给出两个点相连的概率。
6,54张牌,平均分成三堆,大小王在同一堆的概率?
Solutions:
1, 0.25
假设整体长度为1(因为这个值不影响概率的计算,所以可以这样假设),第一段的长度是x,第二段为y,第三段为1-x-y。
x,y值要想成为木棍切出来的长度必须要满足的条件为 0<x<1, 0<y<1,0<x+y<1,这些点构成了下图1中红色的部分。
而这三段要构成三角形还必须满足:
x+y>1-x-y => x+y>0.5
x+1-x-y>y => y<0.5;
y+1-x-y>y => x<0.5
这些点构成图2中黄色区域。黄色区域与红色区域面积的比值就是,所有切割中能构成三角形的切割方式和所有切割方式的比值。也就是题目的答案。

2,这种一种概率模型?叫啥来着
因为每次抛到6的概率相等,都是1/6,于是期望的次数就是1/(1/6)=6次。
3,一个木桶里面有M个白球,每分钟从桶中随机取出一个球涂成红色(无论白或红都涂红)再放回,问将桶中球全部涂红的期望时间是多少?
这题目和上面的用到了同样的概率模型。
在M个球中取到第1个未着色的取得次数期望是:1
在M个球中取到第2个未着色的取得次数期望是:1/(M-1/M) ---- 这就是用题目2的模型得出的期望,就像抛色子(只有两色),第一个着色的点数为1,其它所有未着色的是点数为2。
在M个球中取到第3个未着色的取得次数期望是:1/(M-2/M)
...
在M个球中取到第M个未作色的求所需要的取得次数的期望是:1/(1/M)
整体次数的期望就是 1+ 1/(M-1/M)+1/(M-2/M)+...+M
4,
用a[i]表示从第i-1级升到第i级期望使用的宝石数量。
当i<=5时,因为不会降级,则期望的数量均为2,即a[2] = a[3] = a[4] = a[5] = 2
当i>5时,因为会降级,成功时一个宝石就够了,不成功时需要倒退一级,需要先使用a[i-1]个宝石先回到i-1级,再使用a[i]个宝石升到第i级,即
a[i] = 1 * 1/2 + (1 + a[i-1] + a[i]) * 1/2
即 a[i] = a[i-1] + 2
可知,a[6]= 4, a[7] = 6, a[8] = 8, a[9] = 10
则1级到9级需要的宝石数为 a[2]+…+a[9] = 36。
5,(only my solution, maybe it's not right...)
n个顶点可以有N=n*(n-1)/2条边,所以这个问题与问题:进行N次实验,每次实验的结果符合伯努利分布,成功的概率为p(未知),N次实验总的成功(平均)次数为m,那么p是多少?是相同的。设随机变量A表示N次伯努利实验成功的次数,Ai表示第i次实验的结果,P(Ai=0)=p,那么A=A1+A2+... 。m=E(A)=E(A1)+E(A2)+.. 。而且E(Ai)=p,所以很容易就求出p来了。
6,
在高中时,这种题太小菜了!!可惜我已经高中过去七八年了~~~
随机事件A: 小王和大王在同一堆
随机事件Ai:小王和大王在第i堆, i=1,2,3 。 A1,A2和A3互斥
P(A)=P(A1+A2+A3)=P(A1)+P(A2)+P(A3)=P(大王在第一堆,小王在第一堆)+P(大王在第二堆,小王在第二堆)+P(大王在第三堆,小王在第三堆)
=P(大王在第一堆|小王在第一堆)P(小王在第一堆)+P(大王在第二堆|小王在第二堆)P(小王在第二堆)+P(大王在第三堆|小王在第三堆)P(小王在第三堆)
=3*(17/53)*(1/3)
=17/53
----------------------------------------------------------------------------------------------------
1, 给你一个数组,设计一个既高效又公平的方法随机打乱这个数组
2,有一苹果,两个人抛硬币来决定谁吃这个苹果,先抛到正面者吃。问先抛这吃到苹果的概率是多少?
3,快速生成10亿个不重复的18位随机数的算法(从n个数中生成m个不重复的随机数)
Solution1:
1,对于A[i],i=0,1,2,...N,随机在数组A[i,i+1,..N]中挑选一个数字交换到A[i]。
为什么这么做会随机?
证明算法随机,只需证明每个数字分配到每个位置的概率是相等的。
易得,数组0-N位置的任意一个数字到位置0的概率都是1/n
到位置1的概率是(1-1/n)*(1/(n-1))=1/n
解释:P(到位置1)=P(第一次调用随机算法的时候没交换到位置0)P(第二次到位置1|第一次调用随机算法的时候没交换到位置0)
到位置2的概率是(1-1/n)(1-1/(n-1))(1/n-2)=1/n
...
2,A表示随机事件先抛的人吃到苹果,那么
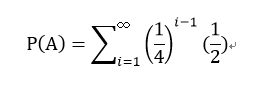
i表示先抛的人一共抛了的次数,上面的式子可以求出,P(A)=2/3
3,