CS231n note
5.1 CNN_history
now:
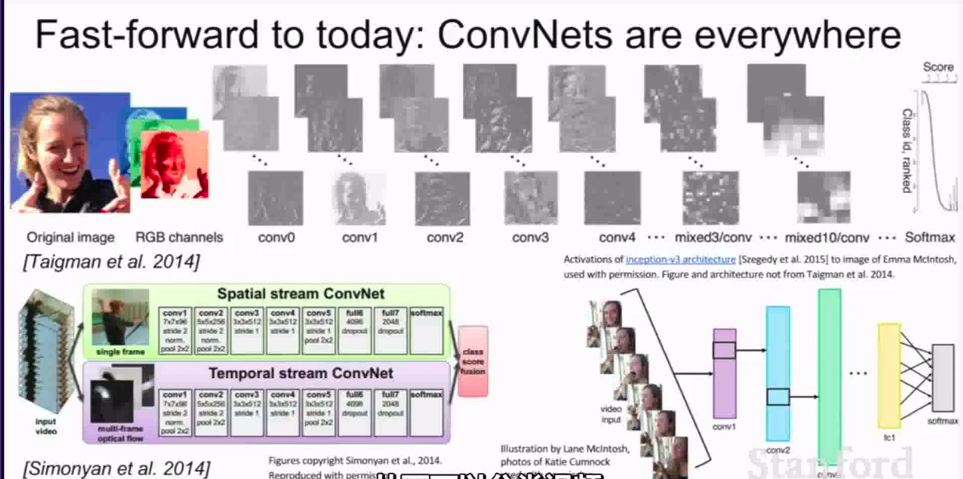
略
5.2 CNN
上节课我们谈到了全连接层的概念:
对于全连接层而言,我们要做的就是在这些向量上进行操作。
例如:
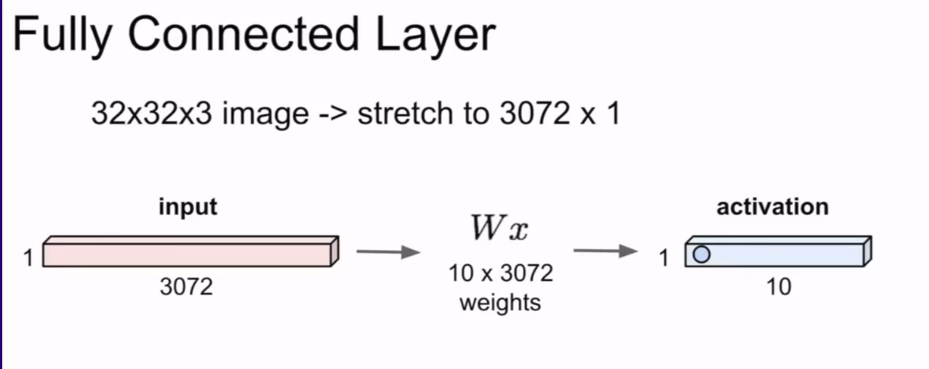
但是至于卷积层,与前者截然不同的地方就是可以保持空间结构
例如下图:
一张32×32×3的图片,我们并非将它展成长向量,而是保持图片的结构。这个三维输入的结构,变成5×5×3
我们将卷积核在图片上滑动,计算出每一个空间定位时的点积结果。
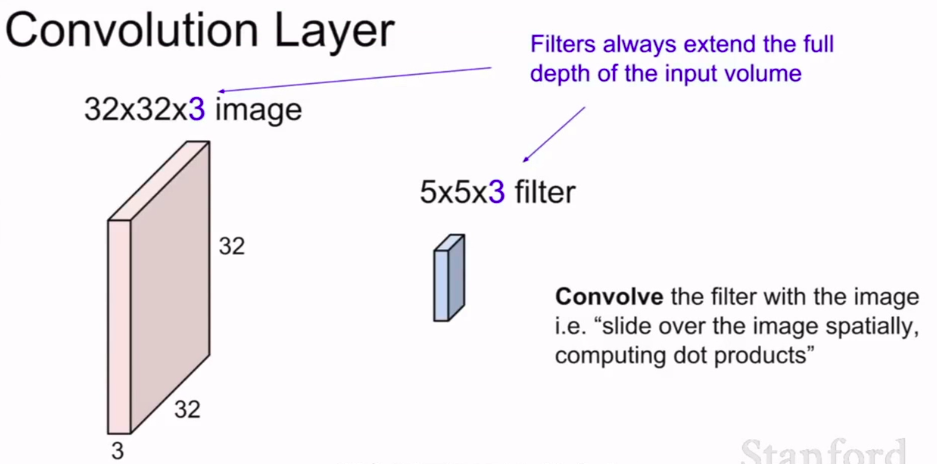
首先我们采用的卷积核总是会将输入量扩展至完全,所以它们一般是很小的区域,比如这里的5×5×3
然后我们用这个卷积核,在图片和卷积核之间进行卷积运算。——我们要做的就是在图片空间区域上覆盖这个卷积核,然后进行点积运算——也就是将卷积核每个位置元素和与之对应图像区域的像素值相乘,这个区域是从图像上取出的。运算之后我们会得到一个点积结果
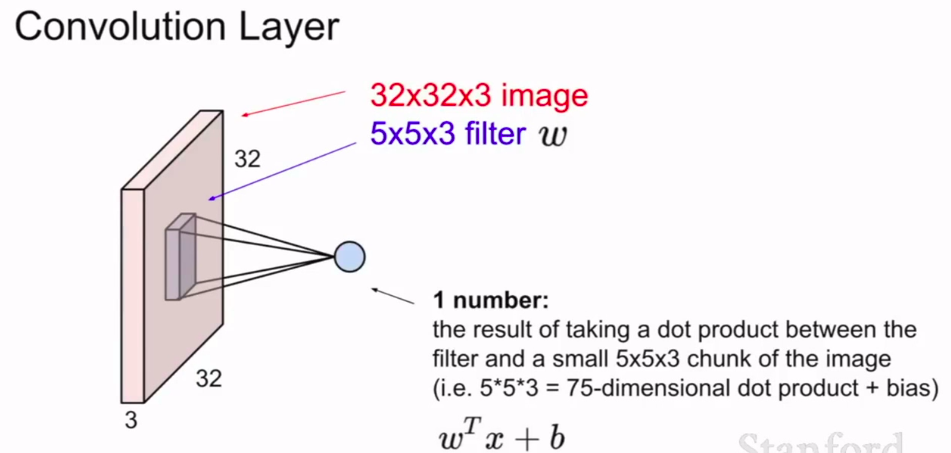
这个例子中,我们进行了5×5×3次运算,这个乘法运算的次数,之后我们再加上偏置项。
接下来我们的问题就是:我们如何滑动卷积核并遍历所有空间位置??
从左上角开始,一直滑动并计算
但我们要先决定:你是否按像素逐个滑动的,或者其他滑动方式。
所以:刚才的例子中,我们采用了一卷积核,然后将它在图像的整个平面进行滑移,然后我们输出它的激活映射。
它里面的值就是卷积核在每个位置求得的结果。
当我们在处理卷积层中,我们希望运用多个卷积核。因为每一个卷积核都可以得到一种特殊的模式或者概念。
所以我们会有一组卷积核。
如图:(一个蓝的一个绿的)
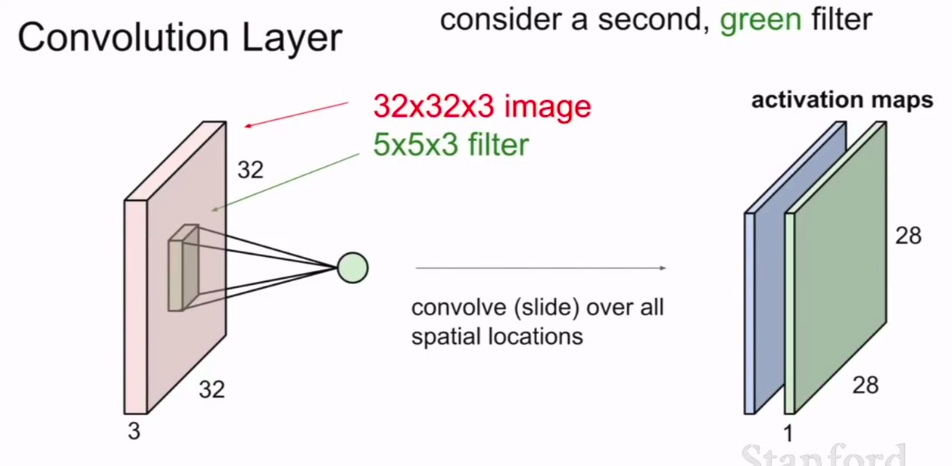
同样我们可以进一步:用6个卷积核
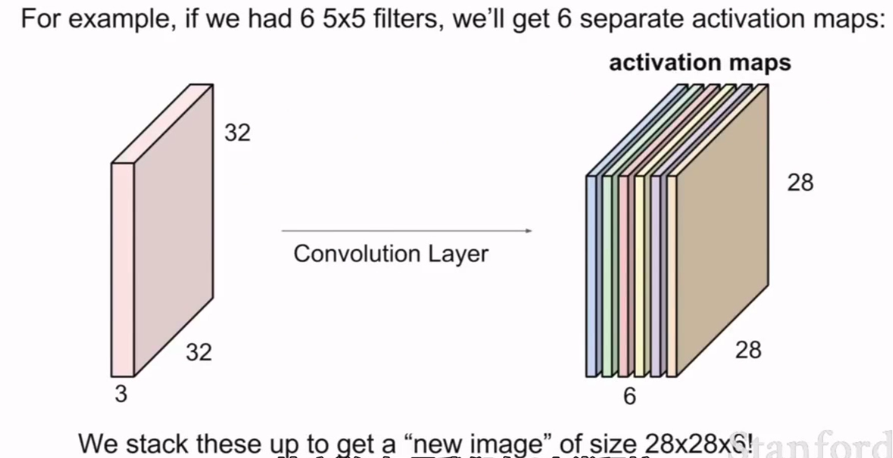
这样我们就得到一个6层的激活映射
我们来描述一下如何在卷积神经网络之中使用这些卷积层?
我们的ConvNet基本上是由多个卷积层组成的一个序列,它们依次堆叠,像是在堆叠简单的线性层一样。
之后我们将用激活函数逐一进行处理
如图:
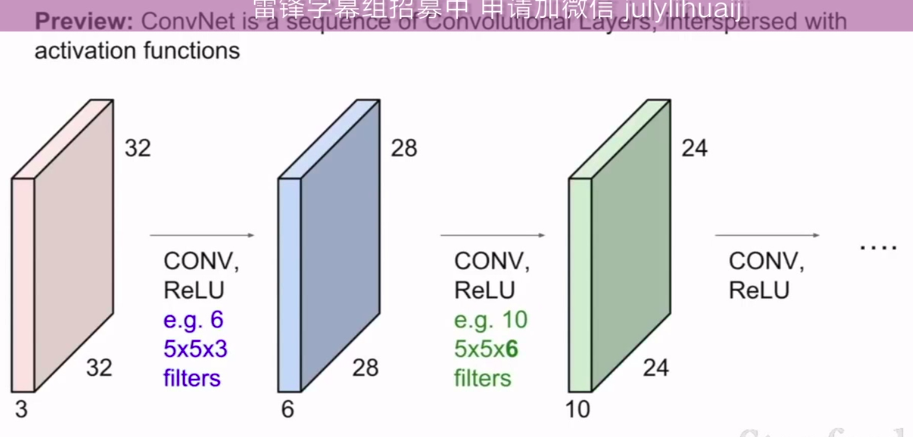
使用多个卷积核,然后每一个卷积核都有一个激活函数
然后结果是你可以把处理好了的叠成一个ConvNet
最后就是学习好了的。

来几个例子:
这是由每个卷积核生成的一些激活函数的例子
当然我们进行了可视化:

例子2:
回到我们第一个的那个32×32×3的图。看看卷积核是如何在图片上滑动并计算的

如图,一直滑动,就像滑动窗口一样。
当然,我们也可以每次滑过2个像素点或者3个之类的。
这取决于实际要求了。
但是,如果我们采用3个像素步伐的话:

这不能匹配!
所以我们要慎重选择!
我们再看一下我们如何计算输出尺寸:可以归纳为一个公式
Output size:
(N - F) / stride + 1
注意,这个公式只有边缘没有被填充的时候才适用
例子:
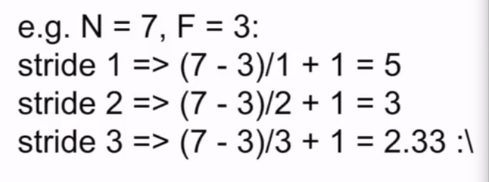
显然,3的时候不能成功。
最后,我们采用0来填充边界来得到最后我们想要的大小。所以这样我们完全可以在左上角放上一个卷积核
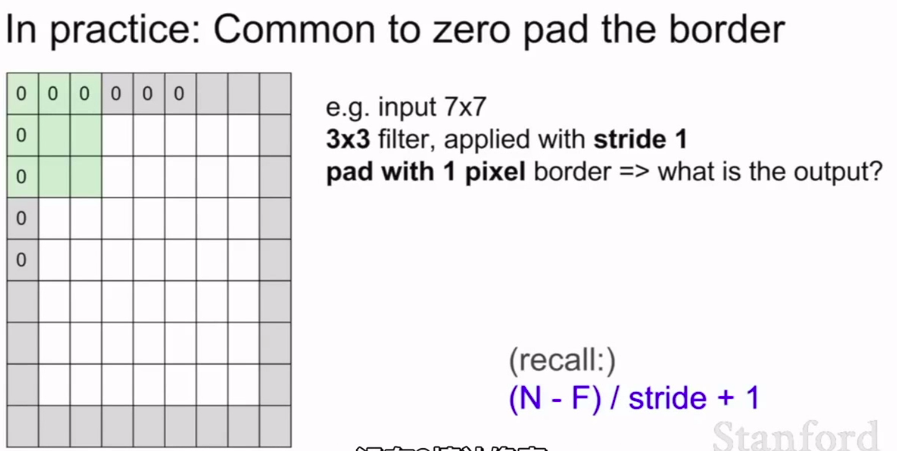
(7 - 1) / 1 + 1 = 7
若是边缘填充了1圈的话,我们还需要一个新的输出。就变成了 9 了(从图像边缘扫描,每行比原来多扫描了2个单元)
- 问题1: 0填补是否在角落增加了一些而外的特征?
0填补只是我们得到一些值的一种方式,以此来处理那个图像范围的事。当然,我们也可以通过其他方式,比如扩充或者复制等等。 - 问题2:如果我们有非方形图片,我们需要会使用横纵不同的步伐吗?
这没什么问题,但实际上通常是相同的步伐,因为我们一般处理方形的图片。 - 问题3:为什么我们要做0填补?
我们做0填补的方式是保持我们之前的输入大小相同。因为我们用卷积核扫描的时候一般会得到一个尺寸比较小的,但我们又想使之全尺寸输出。
例如在深度神经网络当中,有很多卷积核,这样操作的话会使图片的大小迅速减小,这并不是我们想要的。这会损失一些信息,来表示原始图像。同时,关于图片边角的信息也会失去很多
所以总结一下:要考虑:步长(stride),卷积核(filter),卷积核大小,步长大小,零填充
一般卷积核大小会3×3,5×5,7×7
这都是很常用的
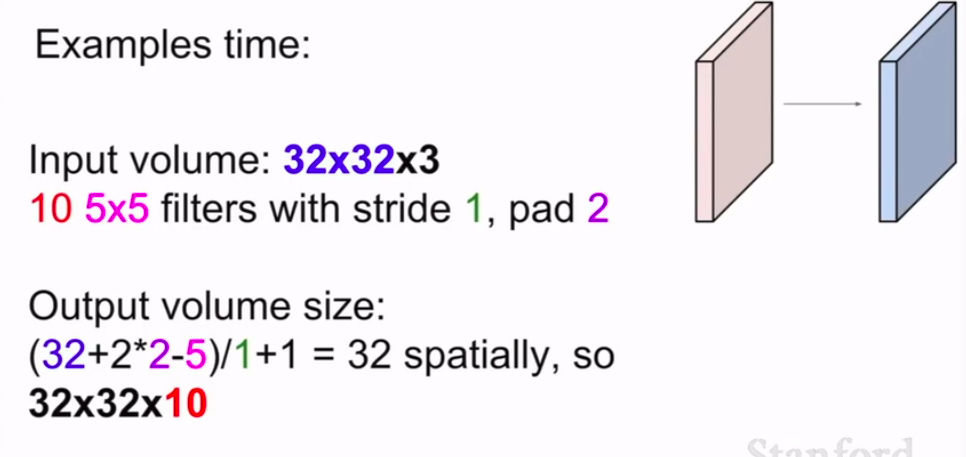
例子:
很容易得到答案。
但是:这一层的参数有多少?
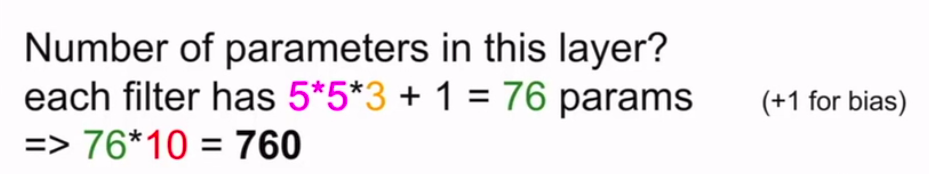
一定要记住我们还有一个偏置项!
总结:

另一方面,我们也可以用1*1的点积

也可以在这个深度上进行计算,但是就是比较麻烦就是 了
最后,我们可以进到caffe或者torch上看看卷积核详细定义