EOJ月赛-OLED【二维前缀和】

C. OLED

单点时限: 2.5 sec

内存限制: 256 MB

OLED 是一种新兴的显示技术。相比于传统 LED 屏幕，可以实现更高的显示亮度、对比度，同时更轻更薄。然而发展至今，OLED 仍然有一个根源性的缺陷：由于 OLED 的每一个像素点单独发光，所以发光时常更长、发光亮度更大的像素，老化速度更快。因此，如果屏幕长时间显示静止的画面，各个像素由于衰减速度不一，时间一长，画面的纹路就好像被烙在了屏幕上。这个现象俗称”烧屏”。

由于现在 OLED 技术的发展，屏幕寿命更加持久，因此烧屏现象不再那么明显。此外，手机厂商也利用了一些软件方面的技术缓解烧屏问题。

屏保（熄屏图像）由于是静止图像，且显示时常非常长，自然是烧屏的重灾区。如今的手机厂商往往会采取以下技术方案：每过一定时间，随机地平移屏保图像。这样，各个像素的发光时常就会更加均匀，不易引发烧屏。

可是，即便如此，烧屏的隐患也没有根本去除。理论上说，虽然屏保图像的位置会移动，但是屏幕上的所有像素的发光时常也不完全均等。只要时间足够长，烧屏依然会发生。Cuber QQ 非常好奇他的手机屏幕在很久以后烧屏情况如何。因此他把他的屏保图像和屏幕尺寸告诉了你，请求出期望的烧屏情况。

为了简化问题，我们规定如下。

屏幕是一个 a 行 b 列（下简称 a×b）的矩阵。屏保图像是一个 （）n×m（1≤n≤a,1≤m≤b） 的黑白图像。1 表示白色，0 表示黑色。当屏保图像显示在屏幕上时，白色对应的像素发光，屏幕上其余的所有像素不发光 （显然， 屏保至少有一点发光， 也就是图像中至少有一个 1）。

每分钟，这个屏保图像会等概率地随机出现在屏幕上的任何一个合法位置（合法位置满足：屏保图像上的每一个像素不超过屏幕边界，图像不缩放，不旋转）。因此学过数学的同学肯定会发现，屏幕一共有 (a−n+1)⋅(b−m+1) 种等概率的显示状态。

Cuber QQ 发现，一个像素的衰减系数和它的发光时长成正比。为了方便后续研究，Cuber QQ 规定屏幕上衰减程度最大（也就是发光时长最长）的像素的衰减系数为 100，其余像素的衰减系数以此为基准可以相应得出。

给定屏幕尺寸和屏保图案，请你求出经过足够长的时间，每一个像素期望的衰减系数。

输入格式

第一行 n,m,a,b (1≤a≤3840, 1≤b≤2160, 1≤n≤a, 1≤m≤b)。

接下来一个 n×m 的 01 矩阵表示屏保图案, 且矩阵中至少有一个 1。

输出格式

输出一个 a×b 的整数矩阵表示每个像素的衰减系数的整数部分 （即将衰减系数从小数向下取整）。根据题目描述，矩阵中的最大值显然为 100。

做法：

　　对于每一个像素矩阵中的‘1’点，可以在一个矩形区域上平移出现在其中任何一个位置

　　换句话说，原像素矩阵中的每一个‘1’，都对大矩阵上某一矩阵的每个点都有一次贡献

　　

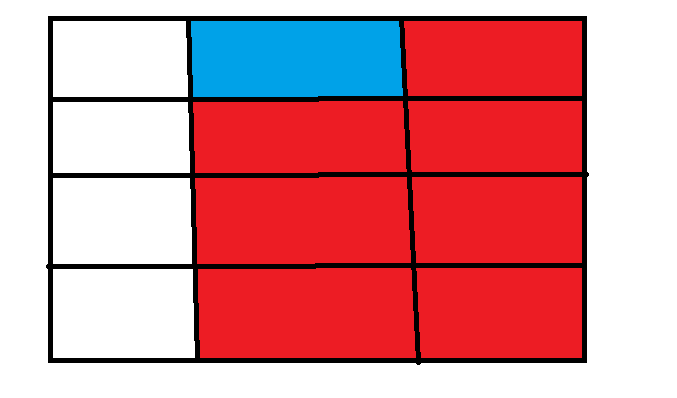
　　　　例如样例1中的这个像素点（1,2），可以通过平移到它右下矩形区域的任一位置，并对这些位置上的像素点有1的贡献

　　 可以想到利用二维前缀和来统计矩阵上每个点‘1’像素出现的次数

　　 通过观察很容易发现当table[i][j] = 1时，此时的‘1’能通过平移出现在（i,j）~（i + a - n, j + b - n）这个矩阵范围内

　　 通过算二维前缀和在O(ab)的复杂度下可以得到每个格子‘1’像素点出现的次数

　　 此时每个点的答案 = 该点出现‘1’的次数 * 100 / max(矩阵中各点‘1’的出现次数）

CODE

#include <bits/stdc++.h>
#define dbg(x) cout << #x << "=" << x << endl
#define eps 1e-8
#define pi acos(-1.0)

using namespace std;
typedef long long LL;

const int inf = 0x3f3f3f3f;

template<class T>inline void read(T &res)
{
    char c;T flag=1;
    while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
    while((c=getchar())>='0'&&c<='9')res=res*10+c-'0';res*=flag;
}

namespace _buff {
    const size_t BUFF = 1 << 19;
    char ibuf[BUFF], *ib = ibuf, *ie = ibuf;
    char getc() {
        if (ib == ie) {
            ib = ibuf;
            ie = ibuf + fread(ibuf, 1, BUFF, stdin);
        }
        return ib == ie ? -1 : *ib++;
    }
}

int qread() {
    using namespace _buff;
    int ret = 0;
    bool pos = true;
    char c = getc();
    for (; (c < '0' || c > '9') && c != '-'; c = getc()) {
        assert(~c);
    }
    if (c == '-') {
        pos = false;
        c = getc();
    }
    for (; c >= '0' && c <= '9'; c = getc()) {
        ret = (ret << 3) + (ret << 1) + (c ^ 48);
    }
    return pos ? ret : -ret;
}

int n,m,a,b;

int table[4000][4000];
int ans[4000][4000];
int sum[4000][4000];

vector<pair<int,int>> v;

int main()
{
    read(n); read(m); read(a);           read(b);
    for ( int i = 0; i < n; ++i ) {
        for ( int j = 0; j < m; ++j ) {
            int x;
            read(x);
            if(x == 1) {
                table[i][j] ++;
                table[i + a - n + 1][j]--;
                table[i][j + b - m + 1]--;
                table[i + a - n + 1][j + b - m + 1]++;
            }
        }
    }
    int temp = -1;
    // for ( int i = 0; i <= a - n; ++i ) {
    //     for ( int j = 0; j <= b - m; ++j ) {
    //         for ( int k = 1; k <= n; ++k ) {
    //             for ( int z = 1; z <= m; ++z ) {
    //                 table[i + k][j + z] += c[k][z];
    //             }
    //         }
    //     }
    // }
    // for ( int i = 1; i <= n; ++i ) {
    //     for ( int j = 1; j <= m; ++j ) {
    //         table[i][j] = c[i][j];
    //     }
    // }
    for ( int i = 0; i <= a; ++i ) {
        for ( int j = 0; j <= b; ++j ) {
            if(i) {
                table[i][j] += table[i - 1][j];
            }
            if(j) {
                table[i][j] += table[i][j - 1];
            }
            if(i && j) {
                table[i][j] -= table[i - 1][j - 1];
            }
            temp = max(temp, table[i][j]);
        }
    }
    // for ( int i = 0; i <= a; ++i ) {
    //     for ( int j = 0; j <= b; ++j ) {
    //         cout << table[i][j] << ' ';
    //     }
    //     puts("");
    // }
    // dbg(temp);
    // for ( int i = 1; i <= a; ++i ) {
    //     for ( int j = 1; j <= b; ++j ) {
    //         cout << table[i][j] << ' ';
    //     }
    //     puts("");
    // }
    // for ( int i = 1; i <= a; ++i ) {
    //     for ( int j = 1; j <= b; ++j ) {
    //         cout << table[i][j] << ' ';
    //     }
    //     puts("");
    // }
    for ( int i = 0; i < a; ++i ) {
        for ( int j = 0; j < b; ++j ) {
            printf("%d ",table[i][j] * 100 / temp);
        }
        puts("");
    }
    return 0;
}