题目描述
给定一个由 nn 行数字组成的数字梯形如下图所示。
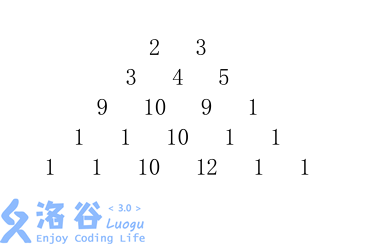
梯形的第一行有 mm 个数字。从梯形的顶部的 mm 个数字开始,在每个数字处可以沿左下或右下方向移动,形成一条从梯形的顶至底的路径。
分别遵守以下规则:
-
从梯形的顶至底的 mm 条路径互不相交;
-
从梯形的顶至底的 mm 条路径仅在数字结点处相交;
-
从梯形的顶至底的 mm 条路径允许在数字结点相交或边相交。
输入格式
第 11 行中有 22 个正整数 mm 和 nn,分别表示数字梯形的第一行有 mm 个数字,共有 nn 行。接下来的 nn 行是数字梯形中各行的数字。
第 11 行有 mm 个数字,第 22 行有 m+1m+1 个数字,以此类推。
输出格式
将按照规则 11,规则 22,和规则 33 计算出的最大数字总和并输出,每行一个最大总和。
输入输出样例
2 5 2 3 3 4 5 9 10 9 1 1 1 10 1 1 1 1 10 12 1 1
66 75 77
说明/提示
1leq m,n leq 201≤m,n≤20
思路
路径问题,关乎点权
以及三种限制条件
很容易想到这就是一个最大费用最大流问题
已经知道了这是一个最大费用最大流问题
就可以着手建图了
因为我们要求一个点权和的最大值
而网络流是无法解决点权的问题的
显然可以把点权转化成边权来做
也就是把一个点拆开成 X,Y 两个点
这个点的点权就是X、Y之间的边权
首先这道题有三个子任务点
(一)、路径互不相交
显然如果要路径互不相交,也就是既没有公共点,也没有公共边
所以,要建出这种限制相当容易,只需要让每个点Xi、Yi之间的流量为1.
且每个点和它下方相连的点的边的流量也应该为1
这样就可以成功限制每个点每条边都只能用一次这个条件
(二)、只能在点处相交
换句话说就是一个点能用多次
所以其他建图条件可以不变,把对点Xi和Yi之间的限制解除即可
(三)、只能在点和边相交
此时就已经完全没有限制条件了
除了超级源向第一行连边依然是1以外
其他所有的边的流量都可以置为无穷
具体详见代码
CODE

1 #include <bits/stdc++.h> 2 #define dbg(x) cout << #x << "=" << x << endl 3 #define eps 1e-8 4 #define pi acos(-1.0) 5 6 using namespace std; 7 typedef long long LL; 8 const int maxn = 1e5 +7; 9 const int inf = 0x3f3f3f3f; 10 11 int n, m, s, t; 12 int head[maxn],pre[maxn],inq[maxn],dis[maxn]; 13 int cnt = 1; 14 int mincost = 0, maxflow = 0; 15 struct edge { 16 int u,to,nxt,w,c; 17 }e[maxn << 1]; 18 19 template<class T>inline void read(T &res) 20 { 21 char c;T flag=1; 22 while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0'; 23 while((c=getchar())>='0'&&c<='9')res=res*10+c-'0';res*=flag; 24 } 25 26 inline void BuildGraph(int u, int v, int w, int cost) 27 { 28 e[++cnt] = (edge){u, v, head[u], w, cost}, head[u] = cnt; 29 e[++cnt] = (edge){v, u, head[v], 0, -cost}, head[v] = cnt;///反向边 30 } 31 32 queue<int> q; 33 34 inline void init() { 35 memset(head, 0, sizeof(head)); 36 memset(pre, 0, sizeof(pre)); 37 memset(inq, 0, sizeof(inq)); 38 memset(dis, 0, sizeof(dis)); 39 memset(e, 0, sizeof(e)); 40 while(!q.empty()) { 41 q.pop(); 42 } 43 mincost = maxflow = 0; 44 cnt = 1; 45 } 46 47 bool SPFA(int x) 48 { 49 memset(inq, 0, sizeof(inq)); 50 for(int i = s; i <= t; i++) { 51 dis[i] = inf; 52 } 53 q.push(x); 54 dis[x] = 0; 55 inq[x] = 1; 56 while(!q.empty()) { 57 int u = q.front(); 58 q.pop(); 59 inq[u] = 0; 60 for(int i = head[u]; i; i = e[i].nxt) { 61 int v = e[i].to, w = e[i].c; 62 if(e[i].w > 0) { 63 if(dis[u] + w < dis[v]) { 64 dis[v] = dis[u] + w; 65 pre[v] = i; 66 if(!inq[v]) { 67 q.push(v); 68 inq[v] = 1; 69 } 70 } 71 } 72 } 73 } 74 if(dis[t] == inf) 75 return 0; 76 return 1; 77 } 78 79 void MCMF() 80 { 81 while(SPFA(s)) { 82 int temp = inf; 83 for(int i = pre[t]; i; i = pre[e[i].u]) { 84 temp = min(temp, e[i].w); 85 } 86 for(int i = pre[t]; i; i = pre[e[i].u]) { 87 e[i].w -= temp; 88 e[i^1].w += temp; 89 mincost += e[i].c * temp; 90 //printf("maxflow:%d mincost:%d ",maxflow, mincost); 91 } 92 maxflow += temp; 93 } 94 } 95 96 int a[1007][1007]; 97 int Depth_Size = 0; 98 99 inline int id1(int a, int b) { 100 return (a-1) * Depth_Size + b; 101 } 102 103 inline int id2(int a, int b) { 104 return n * Depth_Size + (a - 1) * Depth_Size + b; 105 } 106 107 void task1() { 108 //! 3 5 9 10 12 = 39 109 //! 2 4 10 1 10 = 27 110 init(); 111 s = 0, t = n * Depth_Size * 3 + 1; 112 int temp = m + 1; 113 for ( int i = 1; i <= m; ++i ) { 114 BuildGraph(s, id1(1, i), 1, 0); 115 BuildGraph(id1(1, i), id2(1, i), 1, -a[1][i]); 116 BuildGraph(id2(1, i), id1(2, i), 1, 0); 117 BuildGraph(id2(1, i), id1(2, i + 1), 1, 0); 118 //printf("u:%d v:%d cost:%d ",id1(1, i), id2(1, i), -a[1][i]); 119 } 120 for ( int i = 2; i <= n - 1; ++i ) { 121 for ( int j = 1; j <= temp; ++j ) { 122 BuildGraph(id1(i, j), id2(i, j), 1, -a[i][j]); 123 BuildGraph(id2(i, j), id1(i + 1, j), 1, 0); 124 BuildGraph(id2(i, j), id1(i + 1, j + 1), 1, 0); 125 //printf("u:%d v:%d cost:%d ",id1(i, j), id2(i, j), -a[i][j]); 126 } 127 ++temp; 128 } 129 for ( int i = 1; i <= temp; ++i ) { 130 BuildGraph(id1(n, i), id2(n, i), 1, -a[n][i]); 131 BuildGraph(id2(n, i), t, 1, 0); 132 //printf("u:%d v:%d cost:%d ",id1(n, i), id2(n, i), -a[n][i]); 133 } 134 //dbg(t); 135 MCMF(); 136 //dbg(maxflow); 137 cout << -mincost << endl; 138 } 139 140 void task2() { 141 init(); 142 s = 0, t = n * Depth_Size * 3 + 1; 143 int temp = m + 1; 144 for ( int i = 1; i <= m; ++i ) { 145 BuildGraph(s, id1(1, i), 1, 0); 146 BuildGraph(id1(1, i), id2(1, i), inf, -a[1][i]); 147 BuildGraph(id2(1, i), id1(2, i), 1, 0); 148 BuildGraph(id2(1, i), id1(2, i + 1), 1, 0); 149 //printf("u:%d v:%d cost:%d ",id1(1, i), id2(1, i), -a[1][i]); 150 } 151 for ( int i = 2; i <= n - 1; ++i ) { 152 for ( int j = 1; j <= temp; ++j ) { 153 BuildGraph(id1(i, j), id2(i, j), inf, -a[i][j]); 154 BuildGraph(id2(i, j), id1(i + 1, j), 1, 0); 155 BuildGraph(id2(i, j), id1(i + 1, j + 1), 1, 0); 156 //printf("u:%d v:%d cost:%d ",id1(i, j), id2(i, j), -a[i][j]); 157 } 158 ++temp; 159 } 160 for ( int i = 1; i <= temp; ++i ) { 161 BuildGraph(id1(n, i), id2(n, i), inf, -a[n][i]); 162 BuildGraph(id2(n, i), t, inf, 0); 163 //printf("u:%d v:%d cost:%d ",id1(n, i), id2(n, i), -a[n][i]); 164 } 165 //dbg(t); 166 MCMF(); 167 //dbg(maxflow); 168 cout << -mincost << endl; 169 } 170 171 void task3() { 172 init(); 173 s = 0, t = n * Depth_Size * 3 + 1; 174 int temp = m + 1; 175 for ( int i = 1; i <= m; ++i ) { 176 BuildGraph(s, id1(1, i), 1, 0); 177 BuildGraph(id1(1, i), id2(1, i), inf, -a[1][i]); 178 BuildGraph(id2(1, i), id1(2, i), inf, 0); 179 BuildGraph(id2(1, i), id1(2, i + 1), inf, 0); 180 //printf("u:%d v:%d cost:%d ",id1(1, i), id2(1, i), -a[1][i]); 181 } 182 for ( int i = 2; i <= n - 1; ++i ) { 183 for ( int j = 1; j <= temp; ++j ) { 184 BuildGraph(id1(i, j), id2(i, j), inf, -a[i][j]); 185 BuildGraph(id2(i, j), id1(i + 1, j), inf, 0); 186 BuildGraph(id2(i, j), id1(i + 1, j + 1), inf, 0); 187 //printf("u:%d v:%d cost:%d ",id1(i, j), id2(i, j), -a[i][j]); 188 } 189 ++temp; 190 } 191 for ( int i = 1; i <= temp; ++i ) { 192 BuildGraph(id1(n, i), id2(n, i), inf, -a[n][i]); 193 BuildGraph(id2(n, i), t, inf, 0); 194 //printf("u:%d v:%d cost:%d ",id1(n, i), id2(n, i), -a[n][i]); 195 } 196 //dbg(t); 197 MCMF(); 198 //dbg(maxflow); 199 cout << -mincost << endl; 200 } 201 202 int main() 203 { 204 //freopen("data.txt", "r", stdin); 205 read(m); read(n); 206 Depth_Size = m; 207 for ( int i = 1; i <= n; ++i ) { 208 for ( int j = 1; j <= Depth_Size; ++j ) { 209 read(a[i][j]); 210 //printf("a[%d][%d]:%d%c",i, j, a[i][j], j == Depth_Size ? ' ' : ' '); 211 } 212 ++Depth_Size; 213 } 214 task1(); 215 task2(); 216 task3(); 217 return 0; 218 }
