预习笔记
MAP分类器
- 基于后验概率的分类器,后验概率 (p(C_{i}|x)=frac{p(x|C_{i})p(C_{i})}{p(x)})
- 判别方法:(p(x|C_{1})p(C_{1})>p(x|C_{2})p(C_{2})?C1类:C2类)
- 选择后验概率最大的类作为判别结果,即最小化概率误差
贝叶斯分类器
- 由于某些场景中,决策失误付出的实际代价不一样
- 因此在MAP分类器的基础上,引入决策风险的概念,即对每种决策失误赋予对应的权值
- 决策动作(α_i)的决策风险(R(α_{i}|x)=Σ_{j}λ_{ij}p(C_{j}|x)),其中(λ_{ij})表示将真值类别属于j类的样本归于i类的决策的损失
- 对每个样本均归类于其决策风险最小的类别,可使损失期望之和最小化
- 判别方法:(R(α_{i}|x)<R(α_{j}|x)?C_i类:C_j类)
最大似然估计
- 求 (θ_{ML}) 使似然函数 (prod_{n=1}^{N}p(x_{n}|θ)) 最大
- 一般可采用求导数为0点的方法,得到使似然函数取得最大值的(θ_{ML})
- 参数θ被看作确定值,取值为 (θ_{ML})
贝叶斯估计
- 相对于最大似然估计中参数θ是一个确定值,贝叶斯估计将θ也看作随机变量来估计
- 因此需要求参数θ的后验概率(p(θ|D_{i})=frac{p(D_{i}|θ)p(θ)}{p(D_{i})}=αprod_{n=1}^{N_{i}}p(x_{n}|θ)p(θ))(在认为特征间满足独立同分布(iid)时有后一个等式,其中α为归一化因子)
- 再求观测似然关于θ的边缘概率:(p(x|D_{i}))=(int_{θ} p(x|θ,D_{i}))=(int_{θ} p(x|θ)p(θ|D_{i}))
- 随着样本个数的增加,贝叶斯估计越趋于真实的观测似然分布
KNN估计
- 不知道概率分布形式的情况下,估计模式x的概率密度,即以x为中心,在极小区域R内的概率密度函数p(x)
- 设P是任意模式落入R的概率,则有k个样本落入R的概率(p(k)=C_{N}^{k}P^{k}(1-P)^{N-k})
- 由E(k)=NP,N非常大时,有k≈NP,故P≈(frac{k}{N})
- 设R的区域体积为V,则P≈p(x)V,故(p(x)≈frac{P}{V}=frac{k}{NV})
KNN分类器
- 同样基于MAP分类器,但假设观测似然概率基于KNN估计
- 由KNN估计,(p(x|C_i)=frac{k_i}{N_iV},p(x)=frac{k}{NV})
- 又(p(C_i)=frac{N_i}{N})
- 故(p(C_i|x)=frac{p(x|C_i)p(C_i)}{p(x)}=frac{k_i}{k})
- 因此,对于测试样本x,我们找到与其距离最近的k个样本,其中哪个类别的样本最多,就将x归于那一类。即选择最大的(k_i),使得后验概率最大。
直方图估计
- 直方图也是基于无参数概率密度估计的基本原理: (p(x)=frac{k}{NV})
- 将特征空间平均划分为m个格子,每个格子即一个区域R,因此区域R的位置、大小固定。
- 每个格子的统计值为(frac{k_m}{N}) ,其中 N为训练样本个数,(k_m)为落在该格子的训练样本数
- 对于任意模式x,概率密度为统计值/带宽,(p(x)=frac{k_m}{Nh})
核密度估计
- 核密度估计也是基于无参数概率密度估计的基本原理: (p(x)=frac{k}{NV})
- 以任意待估计模式x为中心、固定带宽h,以此确定一个区域R
- 概率密度 (p(x)=frac{Σ_{n=1}^{N}K(x|x_n,h)}{Nh})
复习笔记
贝叶斯决策和MAP分类器
后验概率

MAP分类器
将测试样本决策分类给后验概率最大的那个类
判别公式

决策边界
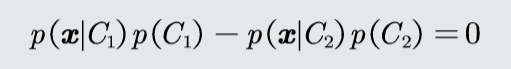
决策误差
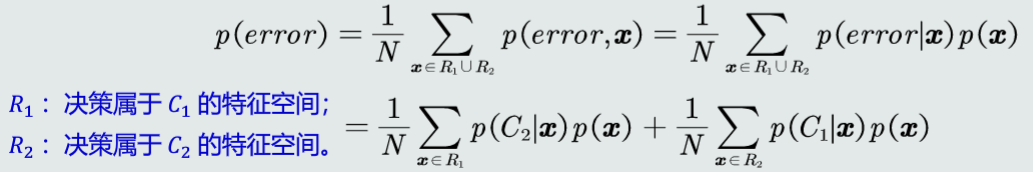
决策风险和贝叶斯分类器
- 决策失误的代价往往不同,因此对每种决策失误给予损失权值,引入决策风险的概念
- 假设该测试样本x的真值是属于(C_j)类,决策动作(a_i)对应的损失可以表达为: (λ(a_i|C_j)), 简写为(λ_{ij})
决策风险

决策目标:最小化期望损失

最大似然估计
目标
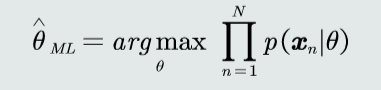
若观测似然概率服从高斯分布
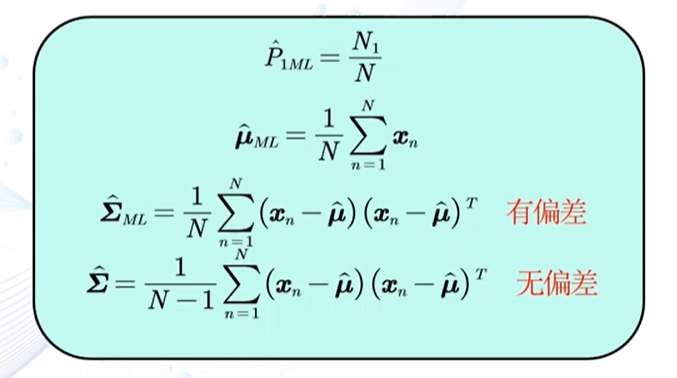
贝叶斯估计
给定参数θ分布的先验概率以及训练样本,估计参数θ分布的后验概率
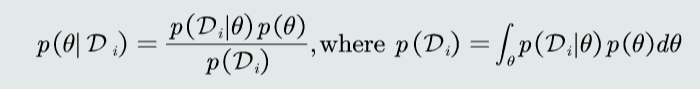
假设样本满足iid条件时
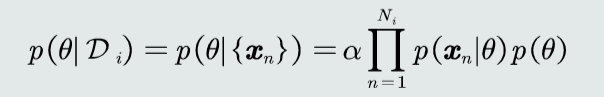
KNN估计
P为落入区域R的概率,k为落入区域R的样本个数
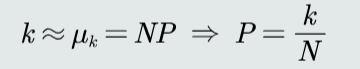
可得p(x)的近似估计,其中V为区域体积
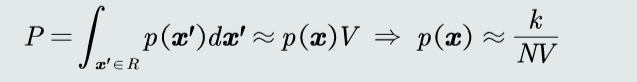
优缺点

直方图与核密度估计
直方图估计
区域R的位置大小固定
每个格子的统计值为(frac{k_m}{N}) ,其中 N为训练样本个数,(k_m)为落在该格子的训练样本数
对于任意模式x,概率密度为统计值/带宽,(p(x)=frac{k_m}{Nh})
优缺点

核密度估计
以任意待估计模式x为中心、固定带宽h,以此确定一个区域R
窗口函数
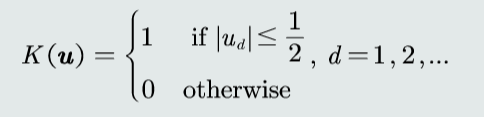
核函数

落入区域的个数k
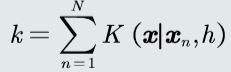
可得概率密度p(x)

优缺点
