论文阅读笔记（十七）【ICCV2017】：Dynamic Label Graph Matching for Unsupervised Video Re-Identification

Introduction

文章主要提出了 Dynamic Graph Matching（DGM）方法，以非监督的方式对多个相机的行人视频中识别出正确匹配、错误匹配的结果。本文主要思想如下图：

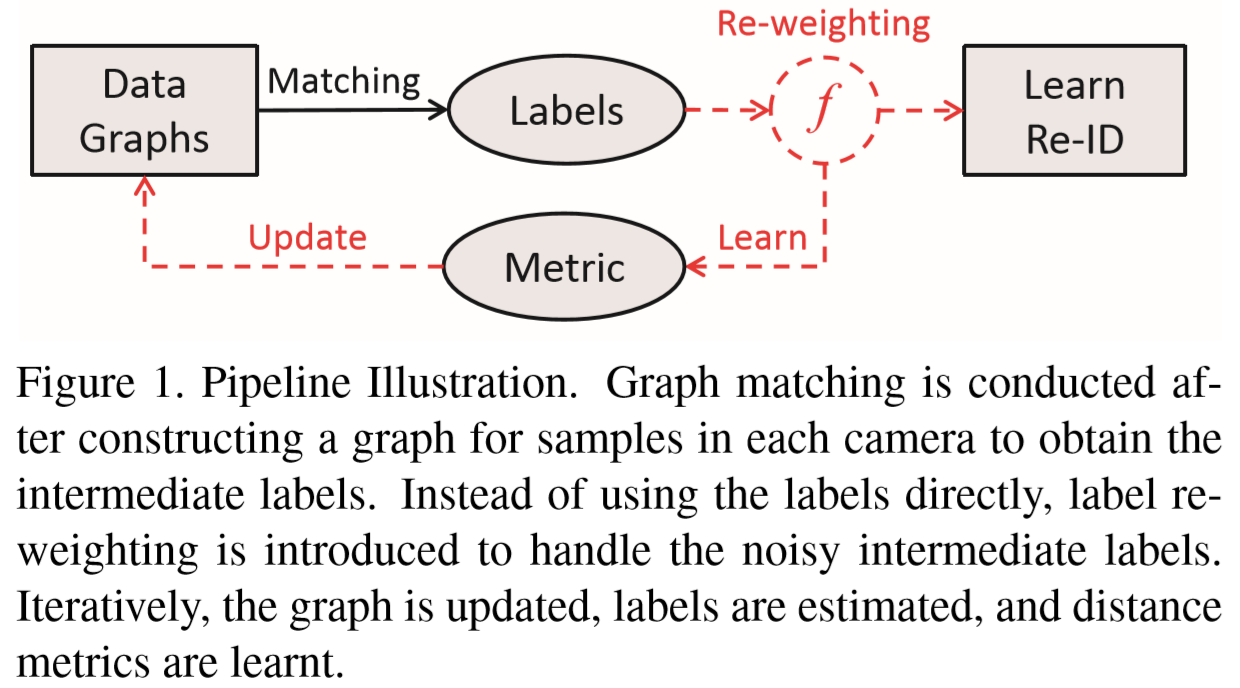
具体而言：方法采用迭代的方式，每次迭代生成一个二部图（bipartite），估计标签并学习区分矩阵。通过不断迭代，标签准确率提高，矩阵区分度更显著。方法加入了重新加权策略（re-weighting），提供软标签而不是硬标签，来降低标签的误差。

Graph Matching for Video Re-ID

（1）挖掘标签信息：

假设相机A拍摄的未标签图 G_A 包含 m 个行人，表示为 [A] = {x_aⁱ | i = 1, 2, ..., m};

相机B拍摄的图 G_B 包含 n 个行人，表示为 [B]₀ = {x_b^j | j = 0, 1, 2, ..., n}，[B]₀ 指除了 n 个元素外包含0元素（为什么加上0元素？）。

目标函数：

其中 y = {y_i^j} 表示 i 和 j 是否表示同一个行人，C = {C(i, j)} 为损失矩阵，其每个元素表示 i 到 j 的距离，计算为：（个人觉得这只是粗略提一下，具体损失函数在下面细说）

（2）惩罚函数：

总体惩罚函数：

Sequence Cost (C_S) 惩罚匹配视频序列之间的差距：

Neighborhood Cost（C_N）惩罚匹配视频邻居之间的差距：

其中和 表示相机A的第 i 个邻居行人和相机B的第 j 个邻居行人（即同一个人），k 为邻居参数，在本实验中 k 设置为5. 

存在约束条件：

其中 和分别是和的邻居；

由于不等式的右侧三项均是很小的正项，因此也是个很小的正项，即： 

Dynamic Graph Matching

（1）标签重新加权：

① positive re-weighting：

对于 y = 1 的项，设置软标签，可以过滤一些误报，然后分配不同的正样本对不同的权重：

② negative re-weighting：

对于 y = 0 的项，设置硬标签，过滤比较明显的负样本对：

其中设置 ，C_m 为 C 的均值，可参照下图进行理解：

 总结：

（2）采用重新加权标签进行矩阵学习：

矩阵学习损失函数：

其中 c₀ 位一个正数，定义为两个相机的平均距离，马氏距离函数为：

矩阵学习目标函数：

其中 w_ij 为平衡正负样本对的平衡因子，如果为正样本对，，如果是负样本对，。

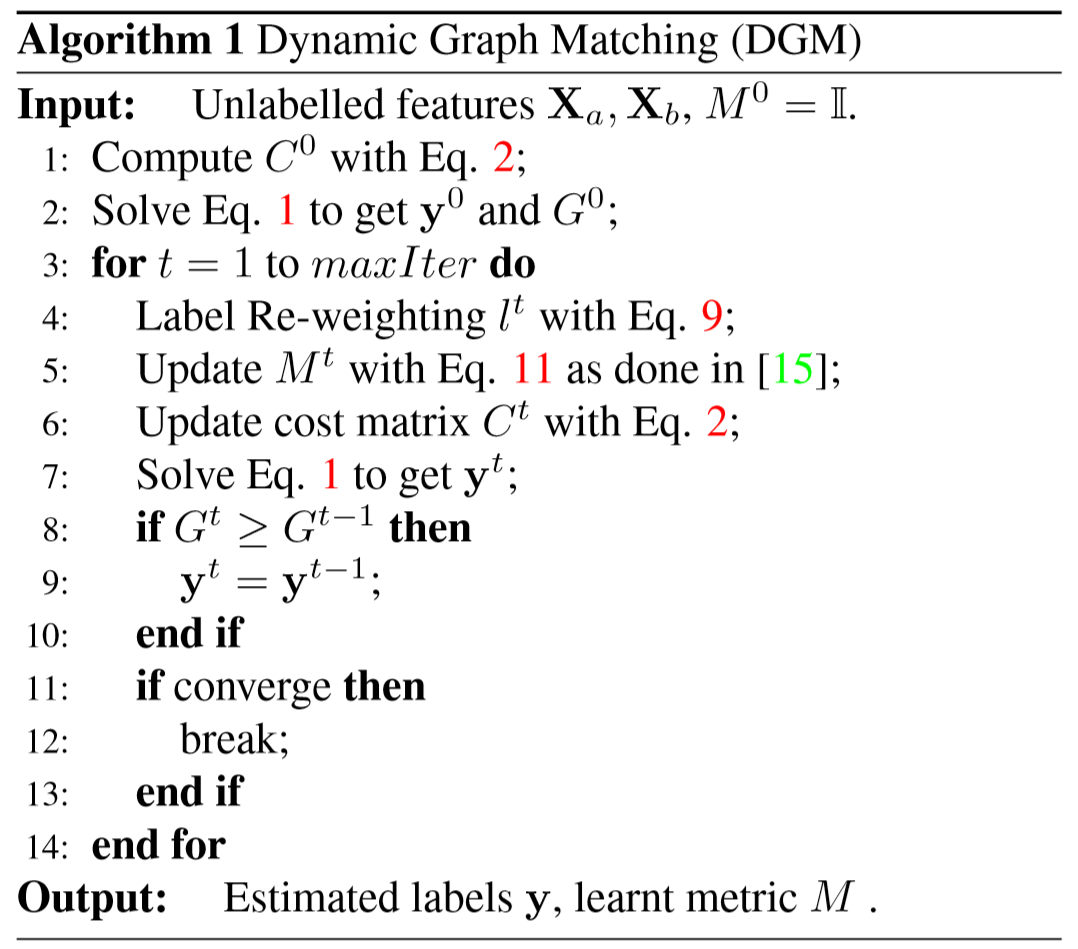
（3）算法描述：

Experiment

（1）实验设置：

① 数据集：PRID-2011、iLIDS-VID、MARS；

② 特征提取：提取帧特征 LOMO，所有图片帧正规化为 128*64，采用PCA方法将特征维度压缩至600维；

③ 参数设置：迭代次数10次，λ = 0.5；

④ 实验环境：PC with i7-4790K @4.0 GHz CPU and 16GB RAM

（2）自我评估：

① 迭代效果：

② 重新加权效果：

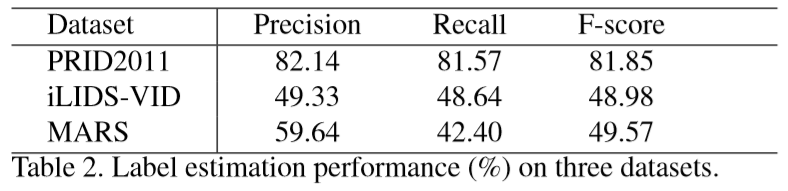
③ 标签评估效果：

（3）对比监督学习：

（4）其他方法对比实验：