1、超参数调试:
(1)超参数寻找策略:
对于所有超参数遍历求最优参数不可取,因为超参数的个数可能很多,可选的数据过于庞大.
由于最优参数周围的参数也可能比较好,所以可取的方法是:在一定的尺度范围内随机取值,先寻找一个较好的参数,再在该参数所在的区域更精细的寻找最优参数.
(2)选择合适的超参数范围:
假设 n[l] 可选取值 50~100:在整个范围内随机均匀取值
选取神经网络层数 #layers,L的可选取值为 2~4:在整个范围内随机均匀取值
学习速率 α 的可选取值 0.0001~1:在对数轴上随机均匀取值
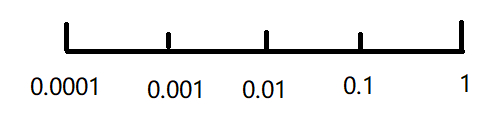
β 的可选取值 0.9~0.999:在 1-β 的对数轴上随机均匀取值
![]()
2、Batch归一化:
(1)问题背景:
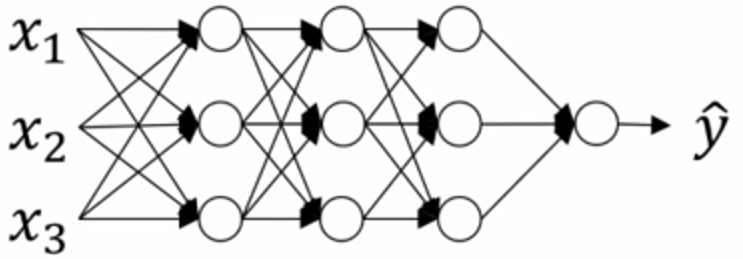
a[1] a[2] a[3]
之前介绍的正则化输入是对 X 进行正则化,那么能否对 a[2] 进行正则化(本质是对 z[2] 正则化),以更快地训练 w[3] 和 b[3] ?
(2)Batch归一化流程:
给出参数:Z(1) ... Z(m)
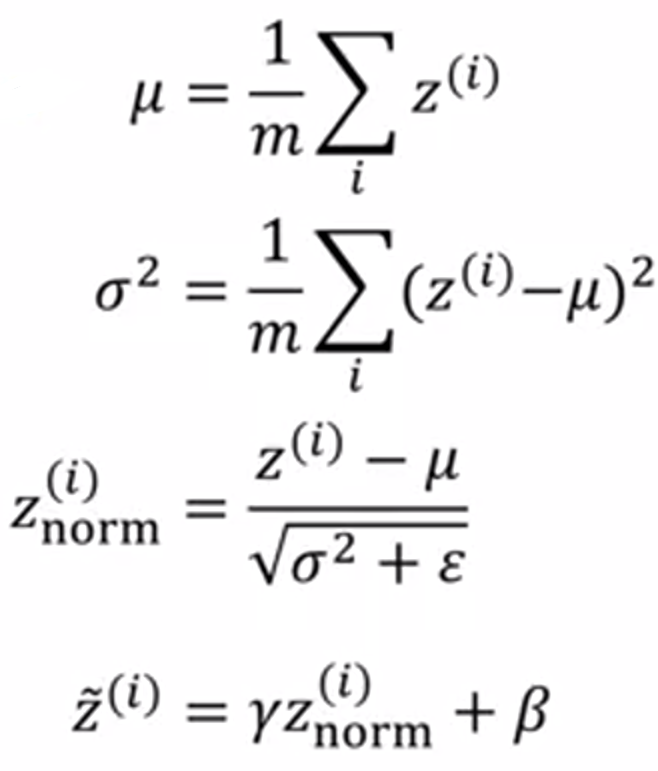
其中 γ 和 β 为学习参数,作用是:可以随意设置 Z~(i) 的平均值和方差.
传播过程:
X — w[1],b[1] —> Z[1] — γ[1], β[1] —> Z~[1] —g(Z~[1]) —> A[1] — w[2],b[2] —> Z[2] — ... —> Y^
需要优化的参数:
W[1], b[1], ..., W[L], b[L]
γ[1], β[1], ..., γ[L], β[L]
一个小的简化:
由于在计算 Z~(i) 前会通过正则化把均值设成0,那么参数 b 可以不用加上.
(3)应用:
for t = 1 ... num_MiniBatches:
Compute forward prop on X{t}
In each hidden layer,use Batch Norm to replace Z[l] with Z~[l]
Use backprop to compute dW[l], dβ[l], dγ[l]
Update parameters W[l], β[l], γ[l]
(Work with momentum、RMSprop、Adam)
3、Softmax回归:
(1)举例说明:
Softmax回归适用于多类别分类,以4分类为例:
神经网络模型:
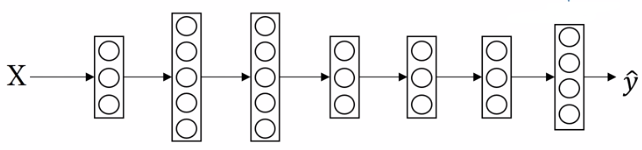
假设 Z[L] = [5, 2, -1, 3]T
t = [e5, e2, e-1, e3]T ≈ [148.4, 7.4, 0.4, 20.1]T
∑ t = 176.3
a[L] = t / ∑ t = [0.842, 0.042, 0.002, 0.114]T
即是分类0的概率是0.842,分类1的概率是0.042,分类2的概率是0.002,分类3的概率是0.114.
(2)Softmax分类器损失函数:
训练结果集:Y = [y(1), y(2), ..., y(m)],每一个 y(i) 都是一个列向量.
预测结果集:Y^ = [y^(1), y^(2), ..., y^(m)]
单个训练样本的损失函数: L(y^, y) = - ∑ yj * log(y^j)
整个训练集的损失函数:J(w[1], b[1], ...) = 1 / m * ∑ L(y^(i), y(i))
4、TensorFlow使用举例:
最小化 J = (w - 5)² = w² - 10w + 25:
(1)写法①:
w = tf.Variable(0, dtype = tf.float32)
cost = tf.add(tf.add(w**2, tf.multiply(-10, w)), 25)
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
init = tf.global_variables_initializer()
session = tf.Session()
session.run(init)
print(session.run(w))
#输出0.0
for i in range(1000):
session.run(train)
print(session.run(w))
#输出4.99999
(2)写法②:
coefficients = np.array([[1.], [-10.], [25.]])
w = tf.Variable(0, dtype = tf.float32)
x = tf.placeholder(tf.float32, [3,1])
cost = x[0][0]*w**2 + x[1][0]*w + x[2][0]
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
init = tf.global_variables_initializer()
session = tf.Session()
session.run(init)
print(session.run(w))
#输出0.0
for i in range(1000):
session.run(train, feed_dicts(x:coefficients))
print(session.run(w))
#输出4.99999