K-Means cluster (K-均值聚类)
1、算法思想:
算法分为两个步骤,簇分配和移动聚类中心。
在每次循环中,第一步是簇分配,即遍历样本,依据更接近哪一个聚类中心,分配到不同的聚类中,如下图所示;
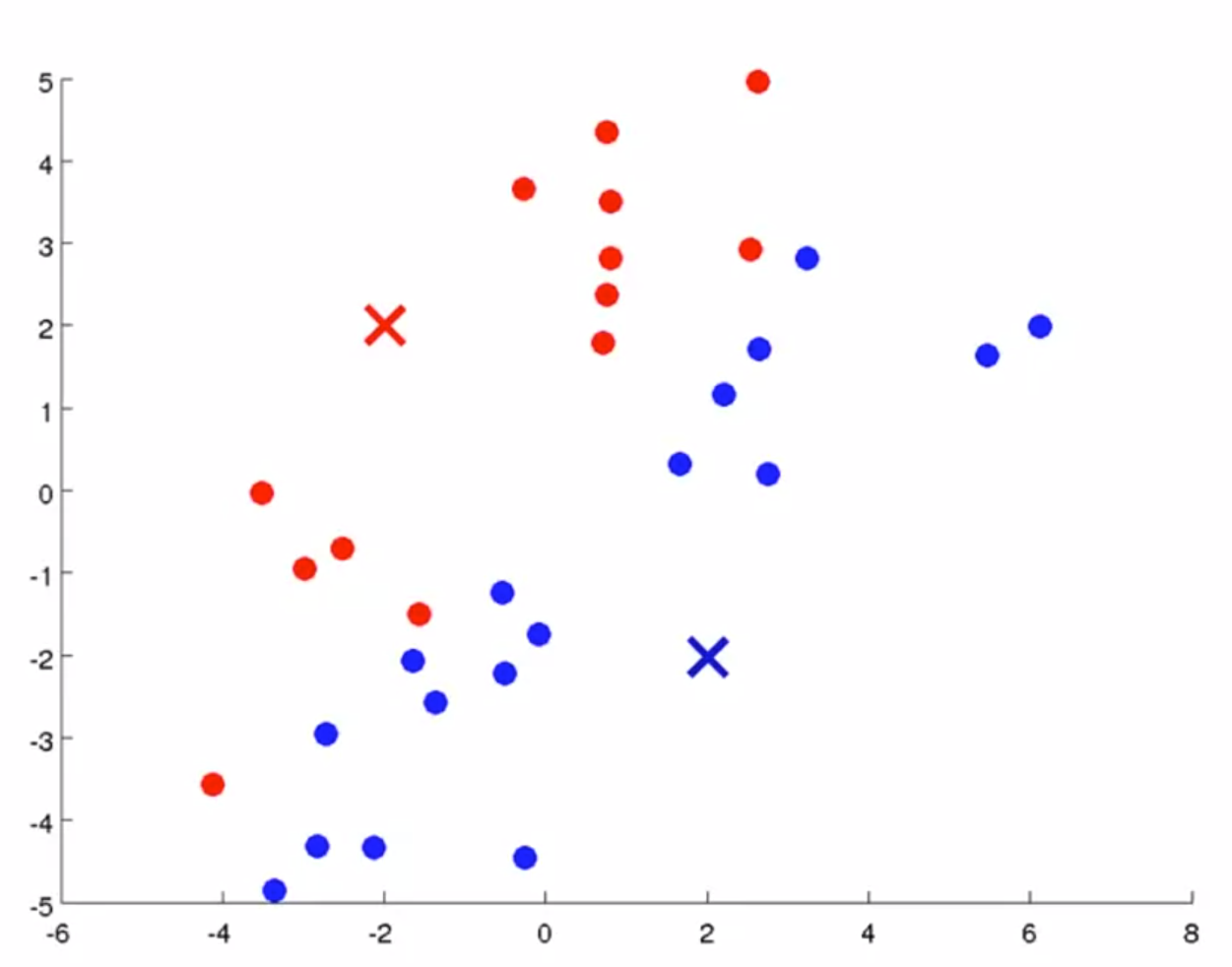
在确定分类后,根据堆点的均值移动聚类中心,如下图所示;

依据新的聚类中心,再次进行簇分配,如下图所示;

如此循环,直到聚类不再变化,即可称为“收敛”。
2、变量表示:
聚类的数量: K
训练集: {x(1), x(2), ..., x(m)} 其中 x(i) 是n维向量,因为不需要额外添加 x0 .
3、算法表示:

4、Optimization objective(优化目标函数):
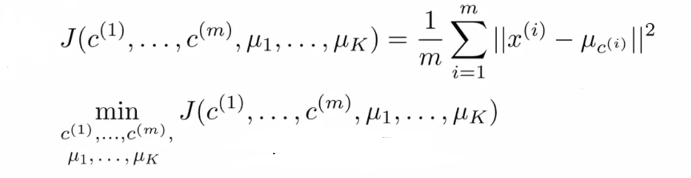
5、Random initialization(随机初始化):
要求 K < m;
随机选取 K 个训练样本作为聚类中心;
设置 μ1, ..., μK 等于这几个样本值,即 μi = xi .
可能存在局部最优的问题:
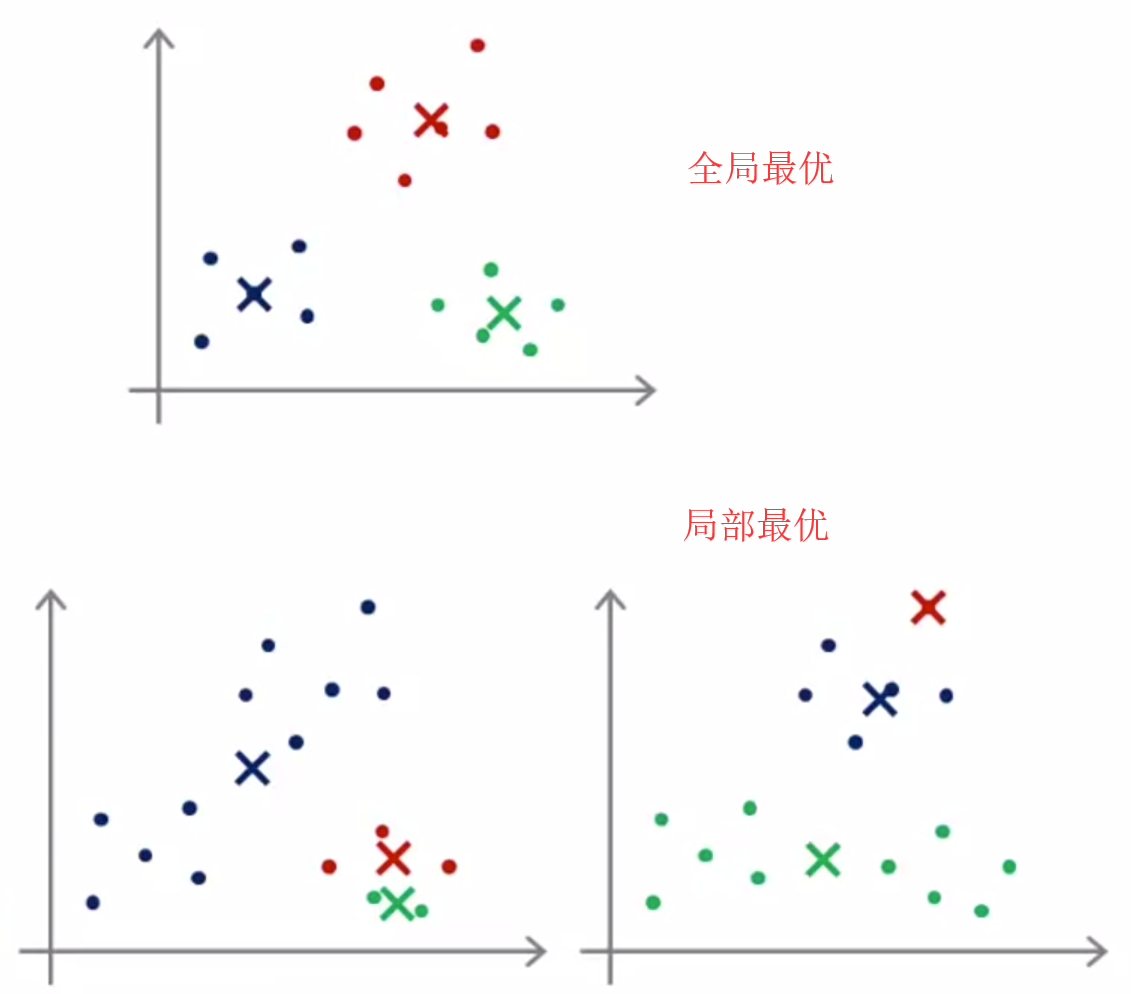
对应方法:多次随机初始化,选出代价最低的一个方法,具体如下:

![]()
6、选择聚类的数量:
(1)方法一:Elbow method(肘部法则):改变 K 的值,计算代价函数 J,绘制对应曲线. 选择曲线的肘点,即代价值下降速度的转折点.
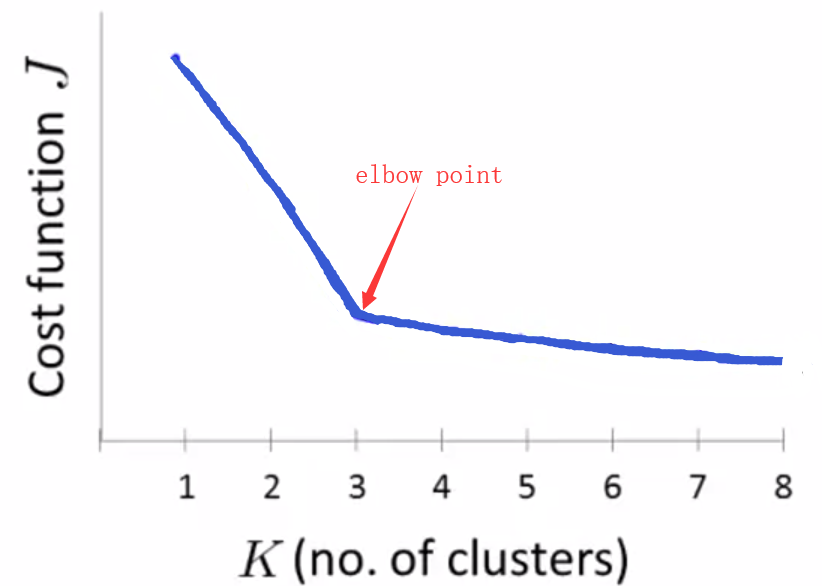
该方法不常用,原因是代价值下降的速度往往很相似,难以区别肘点 .
(2)方法二:依据不同的聚类数量提供的结果优劣.
Dimensionality reduction(维数约减)
1、维数约减的应用:
(1)应用一:数据压缩
将高维的数据映射为低维的数据.
如2维数据映射到一条直线上:

如3维数据映射到一个平面上:

(2)应用二:数据可视化
由于数据只能通过二维或者三维进行可视化,更高维度的数据需要进行压缩处理.
如遇到50维的特征,需要找出一种压缩方法,表示成2维的向量,再进行2D图像的绘制.
2、Principal Component Analysis(主成分分析法 PCA):
(1)问题定义:寻找一组向量,定义一个低维的空间,使得投影误差的平方和达到最小值。
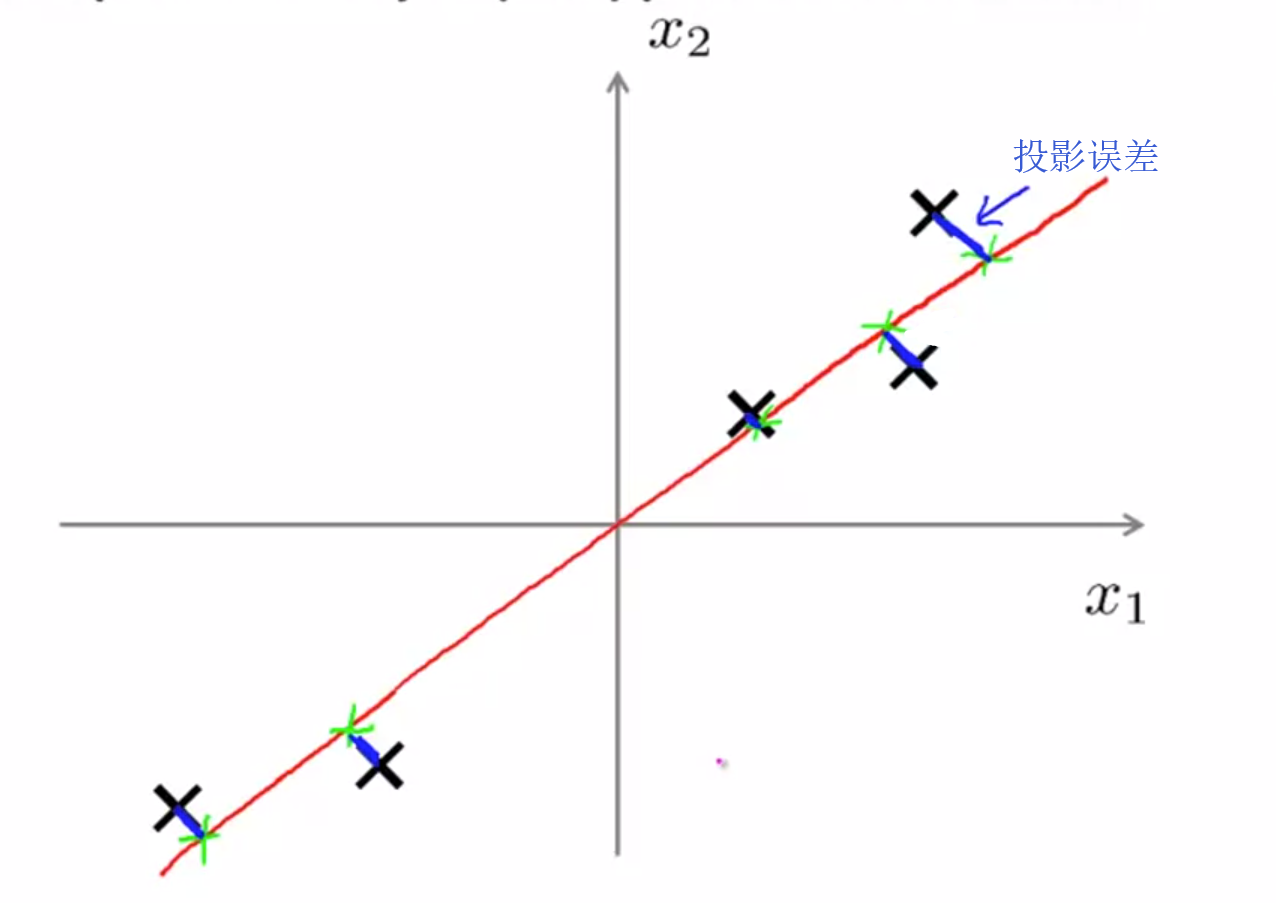
(2)与线性回归的区别:
线性回归:最小化预测值与样本值之间的距离,即 y 的差值;
PCA:最小化样本值和低维空间的距离,即垂线的长度;

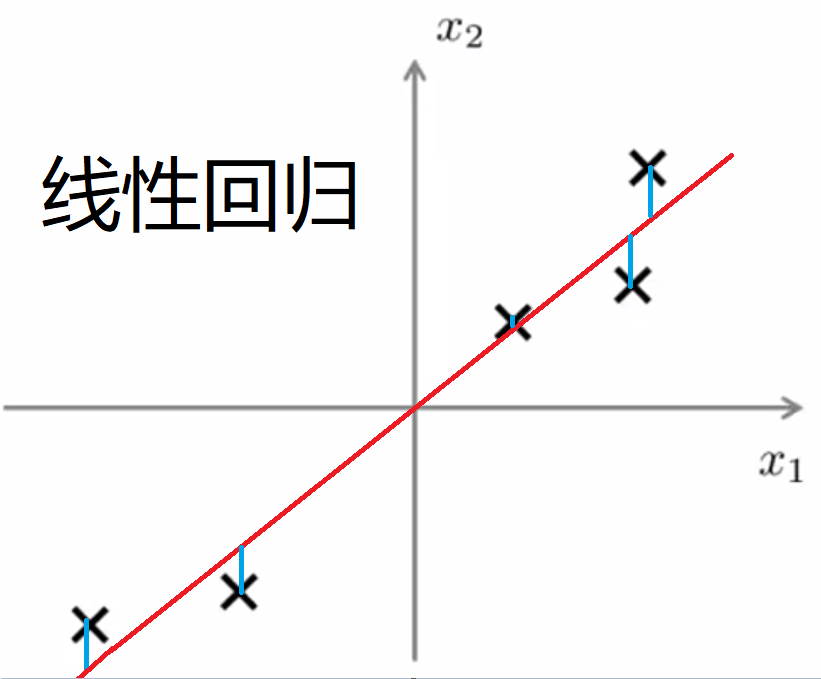
(3)算法流程:
① 数据初始化:对于训练集 {x(1), x(2), ..., x(m)} 进行特征缩放和均值归一化:
计算 μ:![]() ;
;
替换 x:xj(i) = xj - μj,使得所有特征的均值为0;
除以sj:sj 可以用最大最小值或者标准差表示,xj(i) = (xj - μj) / sj .
② PCA算法:将 n 维降低到 k 维
计算协方差矩阵(covariance matrix),记作sigma矩阵:![]() ,规格为 n*n;
,规格为 n*n;
使用svd(singular value decomposition 奇异值分解)函数计算sigma矩阵的特征向量(eigenvector):![]()
其中 U 也为 n*n, U的前 k 列即为所求的k个向量,记作 Ureduce ,即规格为 n*k;;
将获得的 k 列特征向量转置成行向量,计算 Z = UreduceT*X,由于 X 的规格为 n*m,Z 的规格为 k*m;
③ 总结:

什么是协方差矩阵?【传送门】
3、Reconstruction from compressed representation(原始数据重构):
压缩矩阵求法:Z = UreduceT*X
数据重构求法:Xapprox = Ureduce*Z
Xapprox 的每一个点都是原X值的近似点。
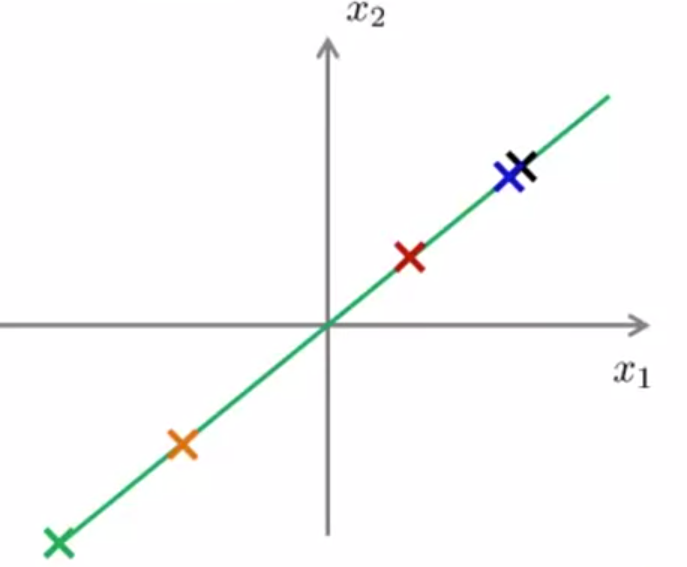
4、选择主成分的数量:
(1)概念:
Average squared projection error(平均平方映射误差):PCA最小化的量;
Total variation(总变差):每一个训练样本长度的平均值(平均来看训练样本距离零向量有多元);
Average squared projection error = ![]()
Total variation = ![]()
选择的k值要满足: (即保留99%的差异性,通常保留95%以上的差异性)
(即保留99%的差异性,通常保留95%以上的差异性)
(2)算法流程:

(3)代码实现:
![]()
其中 S 是一个只有主对角线非零的 n*n 矩阵,其主对角线为[S11, S22, ..., Snn].
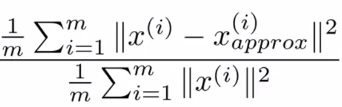
![]()
5、在监督学习中使用PCA提高算法的速度:
① 数据集 {(x(1), y(1)), (x(2), y(2)), ..., (x(m), y(m))},每一个数据 x 是10000维向量;
② 提取出 X,视为不带标签的训练集,即无监督学习,使用PCA算法,转为1000维;
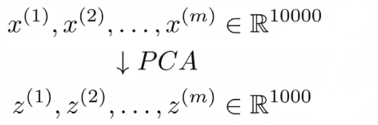
③ 得到新的数据集 {(z(1), y(1)), (z(2), y(2)), ..., (z(m), y(m))}