OpenCASCADE解非线性方程组
eryar@163.com
Abstract. 在科学技术领域里常常提出求解非线性方程组的问题,例如,用非线性函数拟合实验数据问题、非线性网络问题、几何上的曲线曲面求交问题等。OpenCASCADE中有关于非线性方程组定义的类及其求解类,本文主要介绍如何在OpenCASCADE中定义非线性方程组,及对其进行求解。
Key Words. Function Set, Function Set Root, Newton Raphson Algorithm
1.Introduction
在科学技术领域里常常提出求解非线性方程组的问题,例如,用非线性函数拟合实验数据问题、非线性网络问题等。在几何造型中很多问题也可以利用非线性方程组来解决。如曲线的光顺,曲线求交、曲面求交、Blend造型问题等。
OpenCASCADE提供了非线性方程组的类math_FunctionSet,可以先从类图上来看看有哪些算法使用了这个类:

图1 曲线光顺包FaireCurve
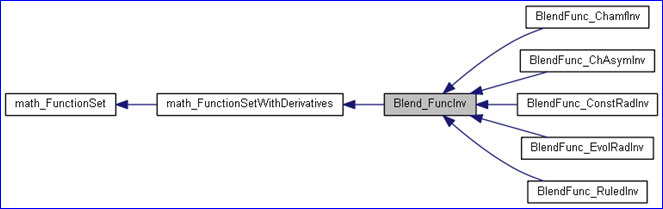
图2 Blending Surface between two surfaces
感兴趣的同学可以自己打开OpenCASCADE的类索引文件查看。可以看到很多算法涉及到方程组的求解问题。本文主要介绍如何定义非线性方程组及对其进行求解。理解这些套路后,对math_FunctionSet相关的派生类及其用用途就会有个清晰的认识,便于对源码的理解。
2.Function Set Definition
设有非线性方程组
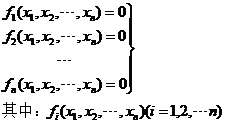
为实变量的非线方程函数。引入向量形式表示,引进记号:

于是非线性方程组可以简单记作:F(x)=0。我们的问题是寻求X使F(X)=0,这个X就是非线性方程组的解。
OpenCASCADE中使用类math_FunctionSet来表示方程组,这是个抽象类,定义了如下纯虚函数:
l NbVariables():变量的个数,即末知量的个数;
l NbEquations():方程的个数,即方程组中有几个方程;
l Value(const math_Vector&X, math_Vector& F):方程组的值,即代入变量每个方程的值;
3.Function Set Root Algorithm
解非线性方程组的牛顿法和解方程式的思路一样,要求方程有一阶导数。而非线性方程组即是要求有偏导数。由fi(x)偏导数作成的矩阵记为J(x)或F’(x),称为F(x)的Jacobi矩阵:

求解非线性方程组的牛顿法为:
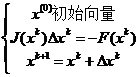
其中xk为方程线的近似解向量。
OpenCASCADE中也提供了非线性方程组的求解类,如:math_FunctionSetRoot,math_NewtonFunctionSetRoot。而使用这些类的输入都是要求具有一阶偏导数的线性方程组的定义math_FunctionSetWithDerivaties。这个类定义了具有一阶偏导数的非线性方程组,其纯虚函数除了前面说明的几个以外,还增加了如下两个:
l Derivatives(const math_Vector& X, math_Matrix& D):一阶偏导数值,即计算Jacobi矩阵;
l Values(const math_Vector& X, math_Vector& F, math_Matrix& D):计算方程的值及一阶偏导数矩阵Jacobi矩阵。
4.Code Example
下面给出一个具体的例子来说明这些类的用法。设有非线性方程组:
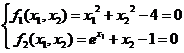
从几何上看其解就是圆心在原点,半径为2的圆与曲线的交点:
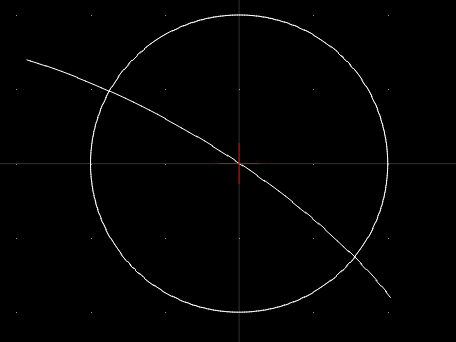
图3 圆与曲线求交
下面我们使用OpenCASCADE来对上述问题进行求解。首先定义这个非线性方程组:
#include <math_FunctionSet.hxx> #include <math_FunctionSetWithDerivatives.hxx> #include <math_FunctionSetRoot.hxx> #pragma comment(lib, "TKernel.lib") #pragma comment(lib, "TKMath.lib") class MyFunctionSet : public math_FunctionSetWithDerivatives { public: virtual Standard_Integer NbVariables() const { return 2; } virtual Standard_Integer NbEquations() const { return 2; } virtual Standard_Boolean Value(const math_Vector& X, math_Vector& F) { F(1) = X(1) * X(1) + X(2) * X(2) - 4.0; F(2) = Pow(M_E, X(1)) + X(2) - 1.0; return Standard_True; } virtual Standard_Boolean Derivatives(const math_Vector& X, math_Matrix& D) { // matrix D is Jacobi matrix. D(1, 1) = 2.0 * X(1); D(1, 2) = 2.0 * X(2); D(2, 1) = Pow(M_E, X(1)); D(2, 2) = 1.0; return Standard_True; } virtual Standard_Boolean Values(const math_Vector& X, math_Vector& F, math_Matrix& D) { Value(X, F); Derivatives(X, D); return Standard_True; } private: }; void test() { MyFunctionSet aFunctionSet; math_FunctionSetRoot aSolver(aFunctionSet); math_Vector aStartingPoint(1, 2); // 1. (1.0, 1.0) aStartingPoint(1) = 1.0; aStartingPoint(2) = 1.0; aSolver.Perform(aFunctionSet, aStartingPoint); if (aSolver.IsDone()) { aSolver.Dump(std::cout); } // 2. (1.0, -1.0) aStartingPoint(1) = 1.0; aStartingPoint(2) = -1.0; aSolver.Perform(aFunctionSet, aStartingPoint); if (aSolver.IsDone()) { aSolver.Dump(std::cout); } } int main(int argc, char* argv[]) { test(); return 0; }
上述代码先定义了带有一阶偏导数的非线性方程组类:MyFunctionSet,因为有两个变量及两个方程,再分别实现计算方程值及偏导数的虚函数。
然后使用类math_FunctionSetRoot来对方程组进行求解,求解的结果如下图所示:
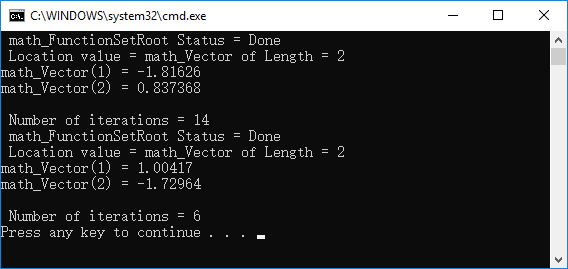
图4 非线性方程组求解结果
由图3可知,两个曲线相交有两个交点,但是使用类math_FunctionSetRoot一次只能计算一个解。从图4的计算结果还可以看出,初值的选择对解的影响很大,既影响计算结果,也影响迭代次数。
5.Conclusion
综上所述,OpenCASCADE的math工具箱中提供了方程组的定义、求解功能。其中对非线性方程组求解使用的是Newton迭代法,所以要求方程组必须实现计算一阶偏导数的虚函数,即计算Jacobi矩阵。
从OpenCASCADE类图中可以看出,方程组定义类用在了很多地方,所以理解上述对方程组的定义及解的用法,对其他使用这个派生类的地方更容易其源码。
6.References
- 同济大学数学教研室. 高等数学 第四版. 高等教育出版社. 2004
- 易大义, 沈云宝, 李有法. 计算方法. 浙江大学出版社. 2002