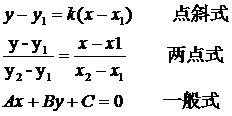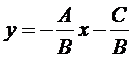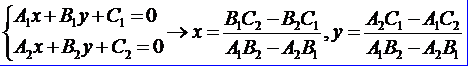Two analytical 2d line intersection in OpenCASCADE

Two analytical 2d line intersection in OpenCASCADE

eryar@163.com

Abstract. OpenCASCADE geometric tools provide algorithms to calculate the intersection of two 2d curves, surfaces, or a 3d curve and a surface. Those are the basis of the Boolean Operation, so under the implementation can help to under the BO algorithms. The paper focus on the intersection of two 2d analytical line.

Key Words. OpenCASCADE, Line Intersection

1.Introduction

在几何造型系统中，通常利用集合的并、交、差运算实现复杂形体的构造，而集合运算需要大量的求交运算。如何提高求交的实用性、稳定性、速度和精度等，对几何造型系统至关重要。当前的几何造型系统，大多数采用边界表示法来表示模型。在这种表示法中，形体的边界元素和某类几何元素相对应，它们可以是直线、圆弧、二次曲线、Bezier曲线和B样条曲线等，也可以是平面、球面、二次曲面、Bezier曲面和B样条曲面等，求交情况十分复杂。在一个典型的几何造型系统中，用到的几何元素通常有25种，为了建立一个通用的求交函数库，所要完成的求交函数多达：

在OpenCASCADE中也有类似的数据结构来表示几何体。本文先来学习最简单的一种求交：两条二维直线的相交。

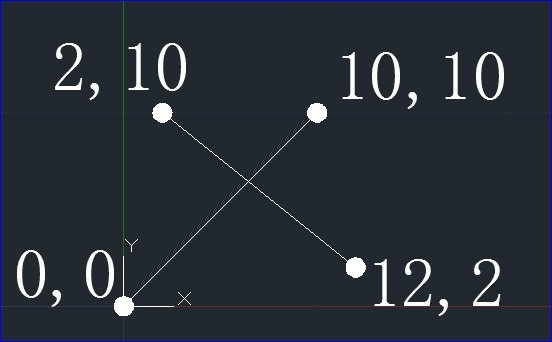
Figure 1. 2d line intersection

2.Code Usage

OpenCASCADE中计算二维解析曲线的类是IntAna2d_AnaIntersection，可用于计算如下的曲线之间的相交：

v 两条二维直线；

v 两个二维圆；

v 二维直线和二维圆；

v 二维直线、圆、椭圆、抛物线、双曲线二次曲线与另外一条二维曲线；

下面使用OpenCASCADE来对图1所示的两条二维直线进行求交计算。代码如下：

/*
Copyright(C) 2017 Shing Liu(eryar@163.com)

Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files(the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and / or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions :

The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT.IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.
*/

// NOTE
// ----
// Tool: Visual Studio 2013 & OpenCASCADE7.1.0
// Date: 2017-02-25  20:52 

#include <gp_Dir2d.hxx>
#include <gp_Lin2d.hxx>
#include <gp_Pnt2d.hxx>

#include <GCE2d_MakeLine.hxx>

#include <IntAna2d_AnaIntersection.hxx>

#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")

#pragma comment(lib, "TKG2d.lib")
#pragma comment(lib, "TKG3d.lib")
#pragma comment(lib, "TKGeomBase.lib")


void test(void)
{
    GCE2d_MakeLine aLineMaker1(gp_Pnt2d(0.0, 0.0),  gp_Pnt2d(10.0, 10.0));
    GCE2d_MakeLine aLineMaker2(gp_Pnt2d(2.0, 10.0), gp_Pnt2d(12.0, 2.0));

    gp_Lin2d aLine1 = aLineMaker1.Value()->Lin2d();
    gp_Lin2d aLine2 = aLineMaker2.Value()->Lin2d();
    
    IntAna2d_AnaIntersection aIntAna;
    aIntAna.Perform(aLine1, aLine2);
    if (aIntAna.IsDone())
    {
        const IntAna2d_IntPoint& aIntPoint = aIntAna.Point(1);
        std::cout << "Number of IntPoint between the 2 curves: " 
                  << aIntAna.NbPoints() << std::endl;
        std::cout << "Intersect Point: " << aIntPoint.Value().X() 
                  << ", " << aIntPoint.Value().Y() << std::endl;
    }

}

int main(int argc, char* argv[])
{
    test();

    return 0;
}

计算得到交点为（6.44, 6.44）：

Number of IntPoint between the 2 curves: 1
Intersect Point: 6.44444, 6.44444
Press any key to continue . . .

3.Code Analysis

计算二维直线相交的代码在文件IntAna2d_AnaIntersection_1.cxx中，其中名字IntAna2d的意思是Intersection Analytical两个单词前三个字母，即二维解析曲线求交包。源码列出如下：

void IntAna2d_AnaIntersection::Perform (const gp_Lin2d& L1,
                    const gp_Lin2d& L2) {

 
  done = Standard_False;

  Standard_Real A1,B1,C1;
  Standard_Real A2,B2,C2;
  L1.Coefficients(A1,B1,C1);
  L2.Coefficients(A2,B2,C2);

  Standard_Real al1,be1,ga1;
  Standard_Real al2,be2,ga2;
  
  Standard_Real Det =Max (Abs(A1),Max(Abs(A2),Max(Abs(B1),Abs(B2))));

  if (Abs(A1)==Det) {
    al1=A1;
    be1=B1;
    ga1=C1;
    al2=A2;
    be2=B2;
    ga2=C2;
  }
  else if (Abs(B1)==Det) {
    al1=B1;
    be1=A1;
    ga1=C1;
    al2=B2;
    be2=A2;
    ga2=C2;
  }
  else if (Abs(A2)==Det) {
    al1=A2;
    be1=B2;
    ga1=C2;
    al2=A1;
    be2=B1;
    ga2=C1;
  }
  else {
    al1=B2;
    be1=A2;
    ga1=C2;
    al2=B1;
    be2=A1;
    ga2=C1;
  }

  Standard_Real rap=al2/al1;
  Standard_Real denom=be2-rap*be1;

  if (Abs(denom)<=RealEpsilon()) {                // Directions confondues
    para=Standard_True;
    nbp=0;
    if (Abs(ga2-rap*ga1)<=RealEpsilon()) {          // Droites confondues
      iden=Standard_True;
      empt=Standard_False;
    }
    else {                                       // Droites paralleles
      iden=Standard_False;
      empt=Standard_True;
    }
  }
  else {
    para=Standard_False;
    iden=Standard_False;
    empt=Standard_False;
    nbp=1;
    Standard_Real XS = (be1*ga2/al1-be2*ga1/al1)/denom;
    Standard_Real YS = (rap*ga1-ga2)/denom;

    if (((Abs(A1)!=Det)&&(Abs(B1)==Det))||
    ((Abs(A1)!=Det)&&(Abs(B1)!=Det)&&(Abs(A2)!=Det))) {
      Standard_Real temp=XS;
      XS=YS;
      YS=temp;
    }

    Standard_Real La,Mu;
    if (Abs(A1)>=Abs(B1)) {
      La=(YS-L1.Location().Y())/A1;
    }
    else {
      La=(L1.Location().X()-XS)/B1;
    }
    if (Abs(A2)>=Abs(B2)) {
      Mu=(YS-L2.Location().Y())/A2;
    }
    else {
      Mu=(L2.Location().X()-XS)/B2;
    }
    lpnt[0].SetValue(XS,YS,La,Mu);
  }
  done=Standard_True;
}

从上述源码中可以看出，OpenCASCADE对二维直线求交计算使用的是解方程组的方法。步骤如下：

v 计算两条直线的系数；

v 计算系数方程组。

这些都是高中数学知识了，就当复习下，并由此看出OpenCASCADE中的一些编码风格。先看第一步，根据点和方向计算二维直线的系数，相关的源码如下所示：

inline void gp_Lin2d::Coefficients (Standard_Real& A,
    Standard_Real& B,
    Standard_Real& C) const
{
  A =   pos.Direction().Y();
  B = - pos.Direction().X();
  C = -(A * pos.Location().X() + B * pos.Location().Y());
}

由高中数学可知，二维直线的方程有三种形式：点斜式、两点式和一般式。

根据一般式方程，当B不等于0时，可得：

因为OpenCASCADE中的gp_Dir2d是单位向量，所以可将其X、Y值分别对应－B和A。确定A和B后，再根据一般式方程将C移项得到：C=-Ax-By

得到直线的系数后，交点的计算就变成如下方程组的求解了：

OpenCASCADE的源码中有多个条件判断，相当于高期消元法中的选主元操作，主要是为了避免分母为0的情况。其中有两个实数直接判断相等的语句，如Abs(A1)==Det这种。对于实数大小的比较，一般总是使用两者相减的值是否落在0的领域中来判断。OpenCASCADE中对于实数的比较没有采用领域比较技术，显得不够严谨。其实领域比较的方法已经在Precison.hxx中进行了说明，只是有些代码没有严格执行。

4.Conclusion

通过对OpenCASCADE中二维直线相交代码的分析，理解其实现原理：将点向式的直线转换成一般式，再对一般式联立方程求解。求解过程中使用了高期消元法的选主元方法。

对于实数的比较应该尽量采用领域比较技术，而避免直接使用两个数相等==或不相等!=的判断。

如果只是判断两条直线是否相交，而不用计算交点的话，《算法导论》中有使用向量来高效算法。

因为二维直线相交只涉及到高中数学知识，所以本文是抛砖引玉，通过继续学习，理解B样条曲线的相交算法实现。

5.References

1. 孙家广, 胡事民. 计算机图形学基础. 清华大学出版社. 2009

2. 人民教育出版社中学数学室. 数学第二册上. 人民教育出版社. 2000

3. 钱能. C++程序设计教程. 清华大学出版社. 2005

4. 易大义, 沈云宝, 李有法. 计算方法. 浙江大学出版社. 2002

5. 潘金贵等译. 算法导论. 机械工业出版社. 2011

PDF Version: Two analytical 2d line intersection in OpenCASCADE