Ensemble Learning
集成学习 就是构造若干模型并用它们的(加权预测/投票)值用于对新样本的预测。类似于多个决策者进行同一个决策。通常来说集成的效果要好于单个模型,当特征,数据,单个模型做到瓶颈时,多模型带来的提升很明显。因此集成学习广泛用于竞赛和实际应用中。集成学习中的单个模型也可以叫做基学习器,基学习器通过现有的学习算法从训练数据中训练得到,常见的如 Decision Tree 与 Neural Network 。衡量集成学习主要有两个指标:
- 准确性:即个体学习器要有一定的准确性,在训练集上正确率至少达到 0.5 才能有好的效果。
- 多样性:即学习器之间要有一些差异,因为完全相同的几个学习器集成起来后完全没有任何效果。
目前集成学习大致分为 Boosting 与 Bagging 两种方式,Boosting 中,基学习器存在强依赖关系,且基学习器是串行执行的,每个基学习器执行完成,更改错误样本的权重分布,以便下一次的基学习器会更加重视这些出错样本;Bagging 即 Bootstrap Aggregation, 即通过 Bootstrap 重采样得到多组训练集,在各个训练集上分别训练一个基学习器,Bagging 中基学习器不存在强依赖关系,各个学习器可以并行化执行。
一个基本问题是 ensemble 为什么 work ?
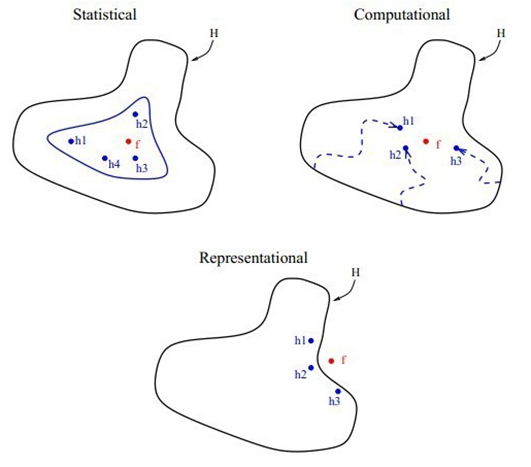
Dietterich 在 ensemble learning in machine learning 中从统计,计算与表示三个方面解释了这个问题,也有人认为这不是真正的“有效性理论基础”,说成是猜想或者直观解释可能更适合。在这之前先复习一下标准的学习理论:
假设样本是从分布 $p(x,y)$ 中采样得到。我们的目标是从所有可能的函数空间 $mathcal{H}$ 中找到最佳的假设函数 $h(x)$ 的, 该模型使得的 loss function 的期望值最小,即:
[h(x) = arg min_{h in mathcal{H}}E[L(h(x),y)|x,y]]
接下来从三个方面分析 ensemble 的有效性:
模型误差 : 通常我们是在子空间搜索(限定模型形式,或者引入先验)而不是在整个空间 $mathcal{H}$ 搜索,因此会带来模型误差。
由于假设空间是人为规定的,在大多数机器学习的应用场合中实际目标假设并不在假设空间之中,如果假设空间在某种集成运算下不封闭,那么我们通过把假设空间中的一系列假设集成起来就有可能表示出不在假设空间中的目标假设。关于表示上的原因比较特别,进一步的说明可以参考.
统计误差 : 因为 $p(x,y)$ 未知,所以只能根据它的一个采样(训练集)来最小化误差,对于一般的学习任务,往往要搜索的假设空间十分巨大,但是能够用于训练分类器的训练集中实例个数不足够用来精确地学习到目标假设,这个时候学习的结果便可能是一系列满足训练集的假设,而学习算法之能够选择这些假设的其中之一作为学习到的分类器进行输出。然而通过机器学习的过拟合问题我们看到,能够满足训练集的假设不一定在实际应用中有同样好的表现,这样学习算法选择哪个假设进行输出的时候就面临着一定的风险,把多个假设集成起来能够降低这种风险(这可以理解为通过集成使得各个假设和目标假设之间的误差得到一定程度的抵消),当采样数目为 $B$ 时:
[Var(frac{1}{N}sum_b L_b)=frac{1}{N} L_b , b = 1,2,...,B]
优化误差 : 在最小化 loss function 时可能是因为使用近似算法或者算法陷入局部最优导致没有收敛到全局最优值带来的误差。
已经证明了在人工神经网络学习和决策树学习中,学习到最好的人工神经网络或者是决策树是一个 NP-hard 问题,其他的分类器模型也面临着类似的计算复杂度的问题。这使得我们只能用某些启发式的方法来降低寻找目标假设的复杂度,但这样的结果是找到的假设不一定是最优的。通过把多个假设集成起来能够使得最终的结果更加接近实际的目标函数值。
虽然以上几方面的原因使得集成学习可能取得更好的学习效果,但是并不是所有的集成方式都有效的,集成学习有效的条件是每个单一的学习器错误率都应当低于 0.5,否则集成的结果反而会提高错误率.
综上,以上的三点原因,现有算法都没有很好的解决,那么通过集成部分弥补标准学习算法的不足, 本文主要讨论了集成学习为什么有效,之后将会继续讨论几种常见的集成学习方法。
参考
ensemble learning in machine learning Dietterich.el