堆是一种图的树形结构,被用于实现“优先队列”(priority queues)
优先队列是一种数据结构,可以自由添加数据,但取出数据时要从最小值开始按顺序取出。在堆的树形结构中,各个顶点被称为“结点”(node),数据就存储在这些结点中。
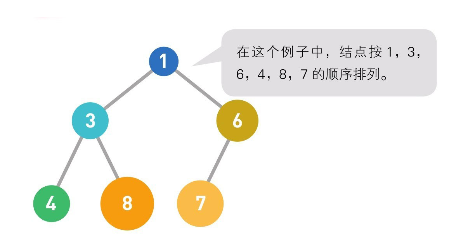
这就是堆的示例。结点内的数字就是存储的数据。堆中的每个结点最多有两个子结点。树的形状取决于数据的个数。另外,结点的排列顺序为从上到下,同一行里则为从左到右。
在堆中存储数据时必须遵守这样一条规则:子结点必定大于父结点。因此,最小值被存储在顶端的根结点中。往堆中添加数据时,为了遵守这条规则,一般会把新数据放在最下面一行靠左的位置。当最下面一行里没有多余空间时,就再往下另起一行,把数据加在这一行的最左端。
试试往堆里添加数字5。寻找新数据的位置。该图中最下面一排空着一个位置,所以将数据加在此处。如果父结点大于子结点,则不符合上文提到的规则,因此需要交换父子结点的位置。这里由于父结点的6大于子结点的5,所以交换了这两个数字。重复这样的操作直到数据都符合规则,不再需要交换为止。这样,往堆中添加数据的操作就完成了。
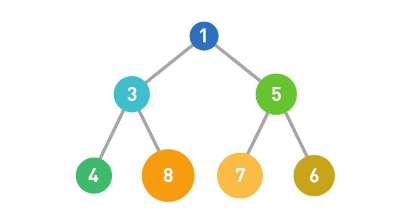
从堆中取出数据时,取出的是最上面的数据。这样,堆中就能始终保持最上面的数据最小。由于最上面的数据被取出,因此堆的结构也需要重新调整。将最后的数据(此处为6)移动到最顶端。如果子结点的数字小于父结点的,就将父结点与其左右两个子结点中较小的一个进行交换。这里由于父结点的6大于子结点(右)的5大于子结点(左)的3,所以将左边的子结点与父结点进行交换。重复这个操作直到数据都符合规则,不再需要交换为止。
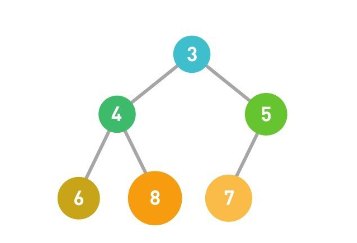
堆中最顶端的数据始终最小,所以无论数据量有多少,取出最小值的时间复杂度都为O(1)。另外,因为取出数据后需要将最后的数据移到最顶端,然后一边比较它与子结点数据的大小,一边往下移动,所以取出数据需要的运行时间和树的高度成正比。假设数据量为n,根据堆的形状特点可知树的高度为log2n,那么重构树的时间复杂度便为O(logn)。
添加数据也一样。在堆的最后添加数据后,数据会一边比较它与父结点数据的大小,一边往上移动,直到满足堆的条件为止,所以添加数据需要的运行时间与树的高度成正比,也是O(logn)。
参考:我的第一本算法书 1-7 堆