前阵子需要用到PID算法控制电机转速，因为之前学的概念都模糊了，所以在网上查了一圈资料，重新学习了下，不过发现很多都是基于文字的描述，很少有通过例子展现算法过程的。这里算是记录,也是给新手理解PID提供多一种思路.
目的:
PID 的重要性应该无需多说了,这个控制领域的应用最广泛的算法了.
本篇文章的目的是希望通过一个例子展示算法过程,并解释以下概念
(1)简单描述何为PID, 为何需要PID,PID 能达到什么作用
(2)理解P(比例环节)作用:基础比例环节
缺点: 产生稳态误差.
疑问: 何为稳态误差 为什么会产生稳态误差.
(3)理解I(积分环节)作用:消除稳态误差.
缺点: 增加超调
疑问: 积分为何能消除稳态误差?
(4) 理解D(微分环节)作用:加大惯性响应速度,减弱超调趋势
疑问: 为何能减弱超调
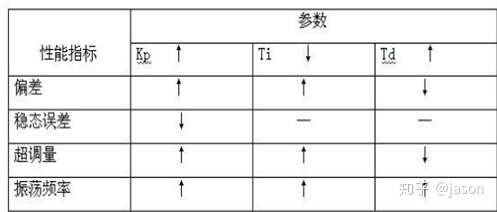
(5)理解各个比例系数的作用
好的下面就开始进入正题吧
一: 何为PID以及为何需要PID
以下即PID 控制的整体框图,过程描述为: 设定一个输出目标,反馈系统传回输出值,如与目标不一致,则存在一个误差,PID 根据此误差调整输入值,直至输出达到设定值.
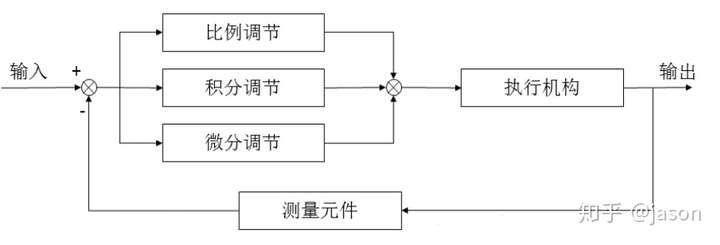
疑问:那么我们为什么需要PID 呢,比如我控制温度,我不能监控温度值,温度值一到就停止吗?
这里必须要先说下我们的目标,因为我们所有的控制无非就是想输出能够达到我们的设定,即如果我们设定了一个目标温度值,那么我们想要一个什么样的温度变化呢.
比如设定目标温度为30度, 目标无非是希望达到图1 希望其能够快速而且没有抖动的达到30度.
那这样大家应该就明白,如果使用温度一到就停止的办法,当然如果要求不高可能也行,当肯定达不到图1 这样的要求,因为温度到了后余温也会让温度继续升高.而且温度自身也会通过空气散热的.
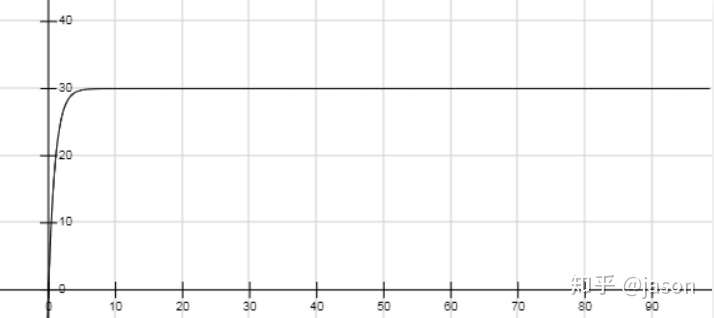图1 系统输出的响应目标
总结: 我们需要PID 的原因无非就是普通控制手段没有办法使输出快速稳定的到达设定值.
如果你扔对此感到疑问,我们就开始用一个常用的例子来具体说明吧
二 一个例子
在开始前,我们需要将我们的公式搬出
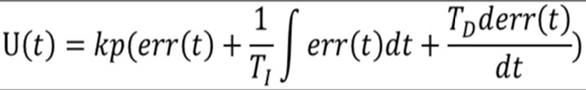
咋一看,这个公式挺唬人的.其实你只要知道微分和积分的基本定义就可以理解.而且最终我们所有的努力也都是能够理解这个公式,否则再精妙的比喻也无法使你真正的明白和使用.
这里我们将其离散化.(如果这步骤有些太快的话,后面再加入对此的解释)
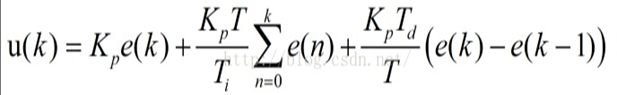
Kp-------比例常数
Ki= (Kp*T)/Ti------积分常数
Kd=(Kp*Td)/T------微风常数
以下我就通过一个例子具体暂时这个方程是如何工作的.
(1) 小明接到一个任务: 有个水桶,需要时刻保持1m 的高度,目前水桶里有0.2m 的水
那么小明采用P(比例) 的方法加水:即每次测量与1m 的误差,并加入与误差成比例的水量
比如设Kp=0.5.
第一次,误差是 1-0.2=0.8m,那么加入水量是 Kp*0.8= 0.4mm.
第二次, 误差是1-0.4 =0.6m 那么加入水量是 Kp*0.6=0.3m
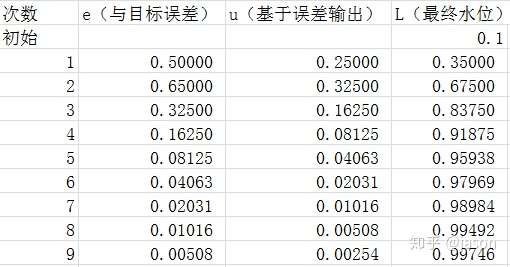
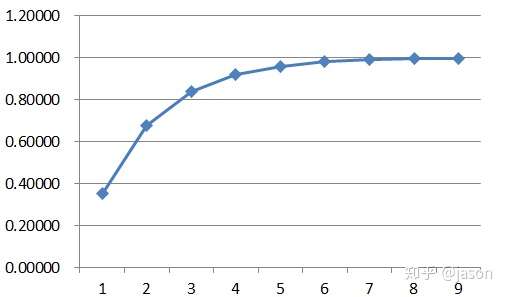
我们发现这太完美了,那么比例环节就能够完美的解决问题了,可是等等,在下这个结论前,我们看小明的新任务
(2)小明的新任务: 有个水桶,但桶底漏了个洞,仍需保持1m 的高度,目前水桶里有0.2m 的水,但每次加水都会流出0.1m. 这个例子就接近我们实际工程的例子了,比如电机摩擦的阻力,损耗.
我们还是来给小明解决问题吧,
第一次仍是使用P (比例控制) u= Kp* e
仍然设Kp=0.5. 则u= 0.5*e
L(最终水位) = 本次输入u 加上上一次水位
第一次,误差是 1-0.2=0.8m,那么加入水量是 Kp*0.8= 0.4mm.最终水位时是0.4+0.2-0.1=0.5
第二次, 误差是1-0.5 =0.5mm 那么加入水量是 Kp*0.5=0.25mm,最终水位是0.5+0.25-0.1=0.65
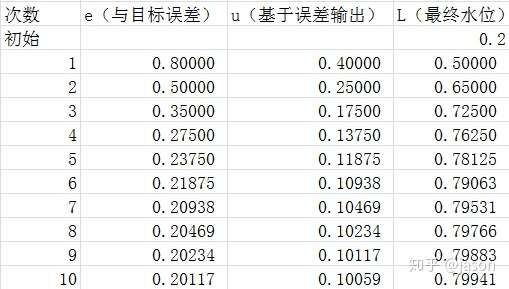表1
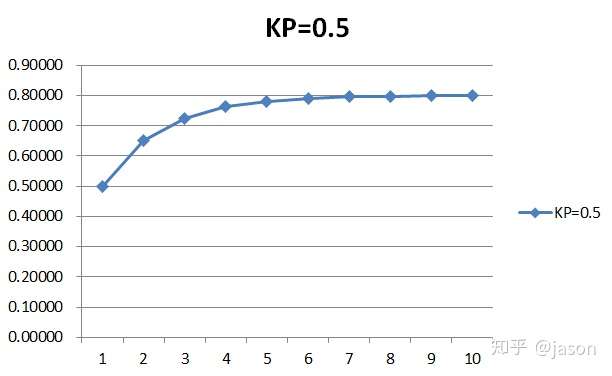
我们发现了问题,水位最终在0.8m 处稳定了,这个也很好理解,当误差是0.2m 时,加水量时0.1,每次加入的刚好等于漏掉的.
这里就引入了稳态误差的概念:即当系统到达稳态时与目标的误差.
那么我们加大Kp 呢.
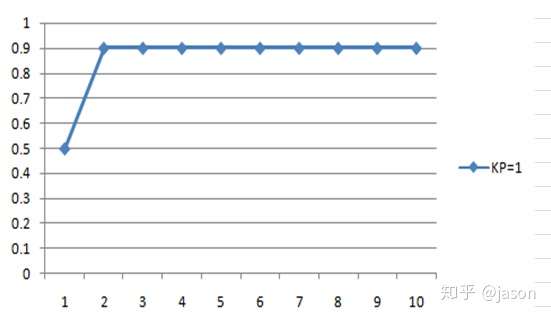
我们发现误差变小了,那我们继续增大吧
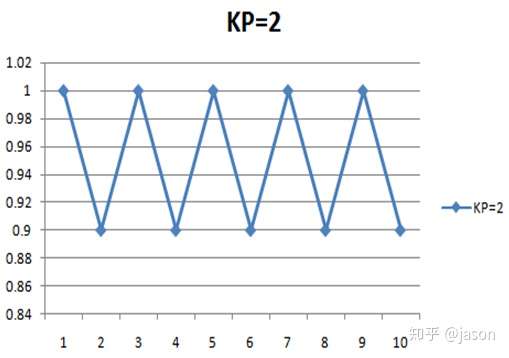
我们发现系统开始震荡了.
此处使用excel 折线图,大家可以调节参数观察变化
结论: 比例控制引入了稳态误差,且无法消除.比例常数增大可以减小稳态误差,但如果太大则引起系统震荡,不稳定.
为了消除稳态误差,第二次加入积分,使用PI(比例积分控制) u=
积分控制就是将历史误差全部加起来乘以积分常数.
这个式子什么意思呢,为啥就能消除稳态误差呢.
还是先设Kp=0.5,Ki= 0.3(这个值我这里是随意设置的)
第一次: 误差为0.8, 比例部分 Kp*0.8=0.4, 积分部分 Ki*(e(1))= 0.24,加入水量u为0.4+0.24=0.64. 最终水位0.2+0.64-0.1= 0.74m
第二次: 误差为0.26,比例部分Kp0.26=0.13,积分部分Kp*(e(1)+e(2))= 0.318,加入水量u为 0.13+0.318=0.448.最终水位 0.74+0.448-0.1=1.088m
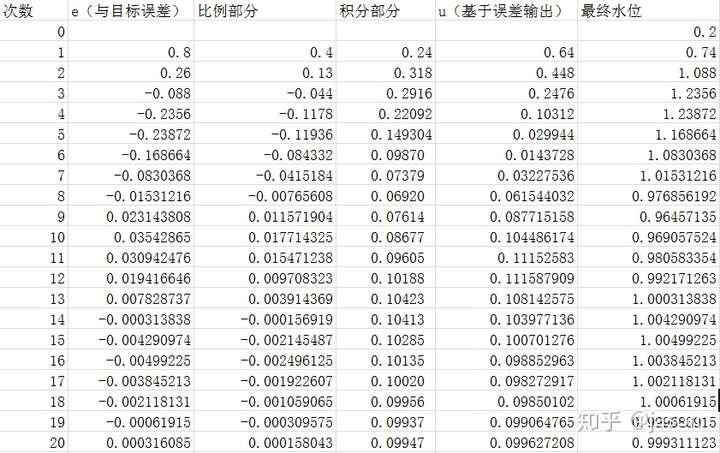表2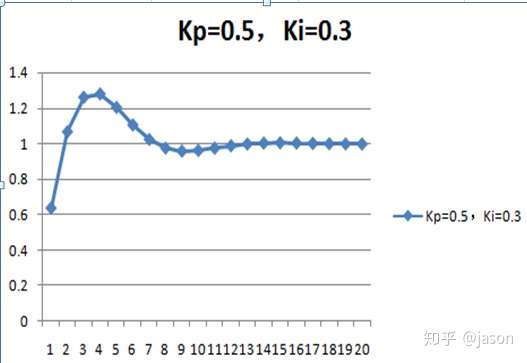
我们发现,虽然过程曲折,但是最终可以稳定到设定值了.
如果 加大Ki 呢
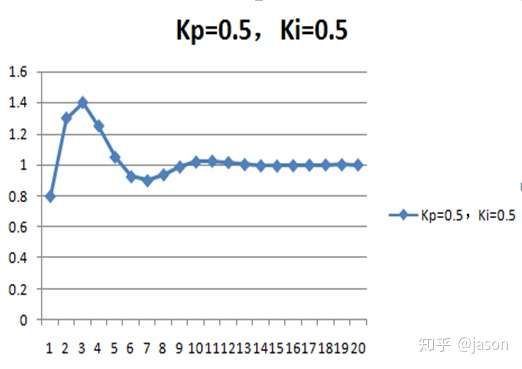
此处使用excel 折线图,大家可以调节参数观察变化
结论:
1 只要存在偏差,积分就不停的累计,直到误差为0, 积分项不再累加,变成一个常数,可以抵消稳态误差.
大家可以看到表2 中系统稳定后,积分项约是0.1.
2 引入积分可以消除稳态误差,但会增加超调,且Ki 增大,超调量也增大.
为了消除超调,我们引入微分作用
现在式子变成了 u=
还是先设Kp=0.5,Ki= 0.5,Kd=0.3
第一次: 误差为0.8, 比例部分 Kp*0.8=0.4, 积分部分 Ki*(e(1))= 0.24,微分部分 =0 (因为没加水前水位差就是0.8) 加入水量u为0.4+0.4=0.8. 最终水位0.2+0.8-0.1= 0.9m
第二次: 误差为0.1,比例部分Kp*0.1=0.5,积分部分Kp*(e(1)+e(2))= 0.45,微分部分为Kd*(e(2)-e(1))加入水量u为 0.5+0.45-0.21=0.29.最终水位 0.9+0.29-0.1=1.09m
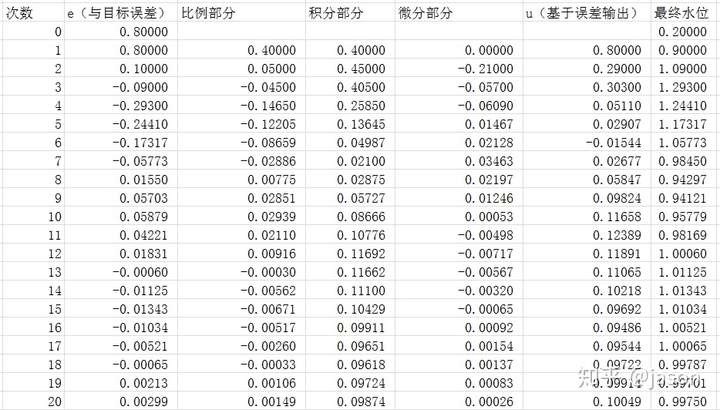表3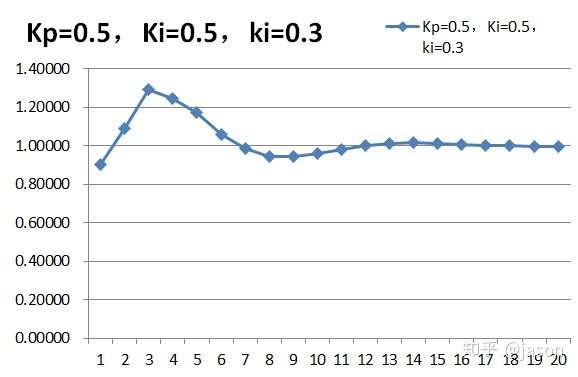
我们发现对比 上面那张Kp= 0.5,Ki=0.5 的图,这张图的震荡减轻了,这正是微分发生了作用,
大家可以看到表3中 当第2次 误差为0.1 时,上一次误差为0.8 时,微分是一个负数,阻止结果快速的变化.
结论: 微分能够减弱超调趋势.
可是,这个波形还是在震荡啊,是的,别忘了,这个值是我随手设置的,我们不能指望我们随便设一个值 就能使 PID 完美的工作起来,如果你自己用excel 模拟一下你就会发现,如果Ki,Kd 设置大些,这个系统会大幅度震荡起来.
因此我们就需要对Kp,Ki,Kd 整定,其实就是试 怎么使输出达到图1 的要求
当然这个例子其实使用PI 就可以了,我们这里是为了理解其作用的原理.
以上,如果有错误的地方请大家及时的指出.