日期:2020.02.12
博客期:152
星期三
老师给的任务都做完了,15篇博客也都写好了,剩下的几天居然还要每天写一篇~唉~为难我 PH ,剩下的几天就把 我的数独要义分享一下吧!
1、基本局规则
数独表是一个 9 X 9 的宫格!其中对这个 81宫格 的每一种划分的区块内,标注着不重复的 1 ~ 9 数字!
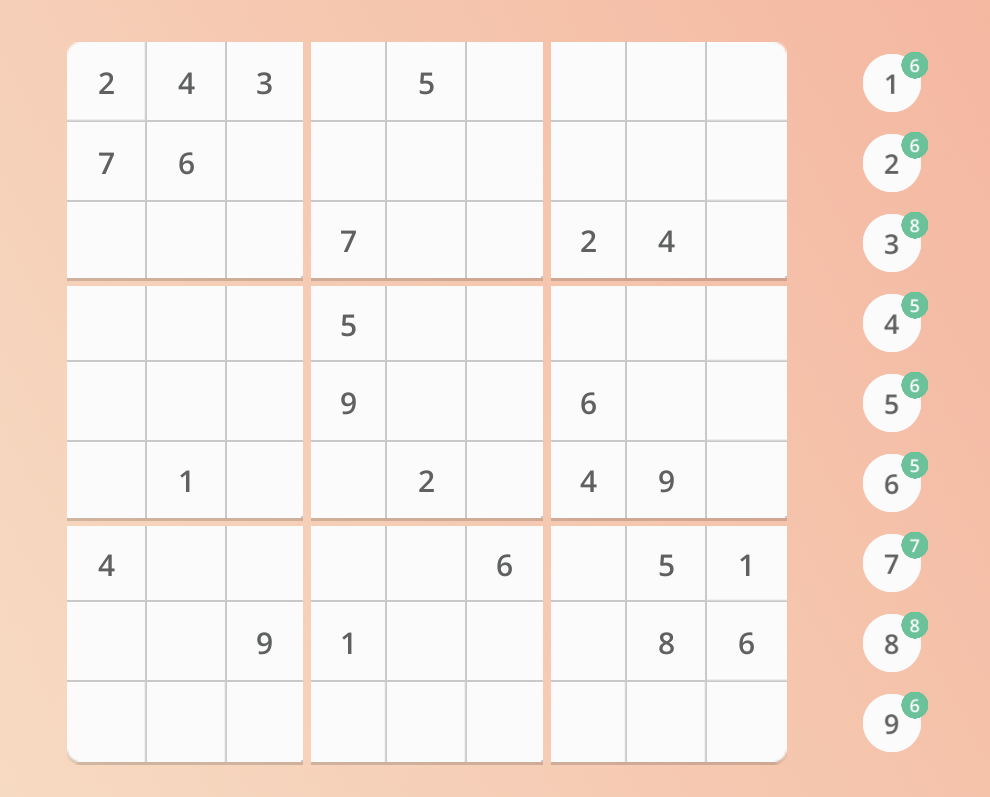
一共有三种划分方法:
第一种——像上面的图一样,中间的粉线把 81 宫格分成了 9 个 九宫格!
第二种——上面的每一行都看作一个区块(上面的八条横线,将 81宫格 划分成 9 行 )
第三种——上面的每一列都看作一个区块(上面的八条竖线,将 81宫格 划分成 9 列)
将上述三种划分的区块里 1~9数字不重复的填入,这就是我们数独游戏的内容了!(其实我不知道怎么玩,也没有看过规则,这是自己总结的)
2、我的开局思路
(a). 首先需要找到表格上未填入的数字每一种有多少个,找到剩余未填数目最少的那一个(如上图就是 6 ,它剩余 5 个是没有填的)
(b). 我们看看有什么地方可以填入 6

(c). 看右上角的九宫格,由于它的下面两个九宫格都有 6,分析得出结论——左上角的 6 应该在 这个九宫格的第 2 列,然后分析行,得出结论——左上角的 6 应该在这个九宫格的第 1 行 或 第 3 行,综上所述 6 的坐标应该是 (1,2) 或 (3,2)位置【九宫格内】!因为 (3,2)位置已经有了数字 4,所以 6 应该在 (1,2)位置。
(d). 同理,找到其余结果。(剩下的两个九宫格里的 6 没有办法找到,因为是有 2 种可能,所以我们只标记一下)
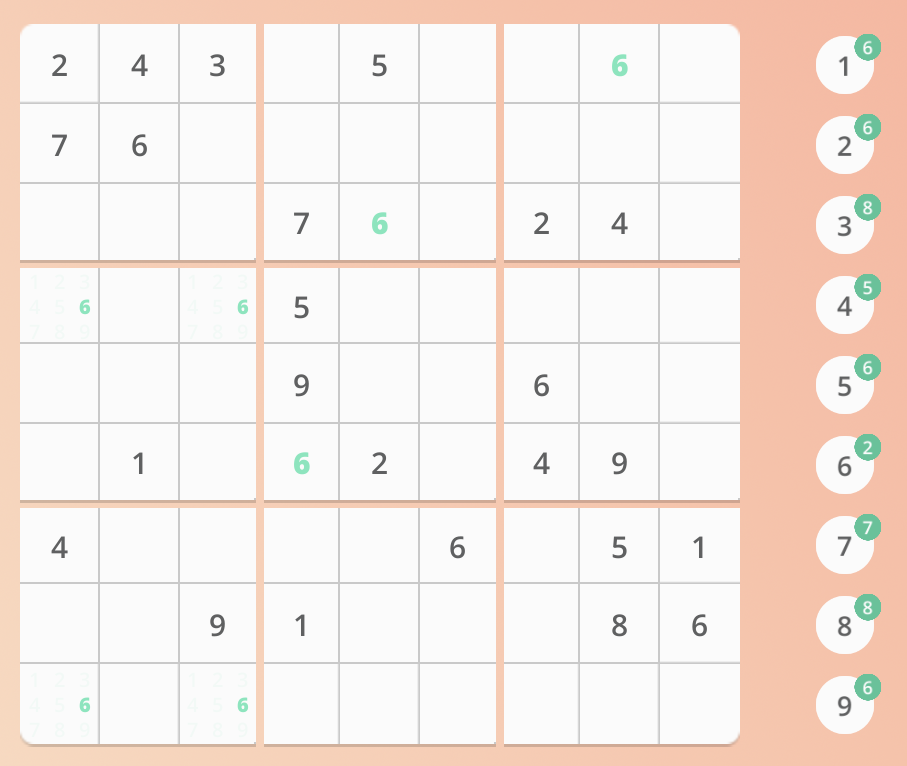
(e).可以继续选择去找下一个(除了已经处理过的 6 以外)剩余数目最小的数字,去操作。
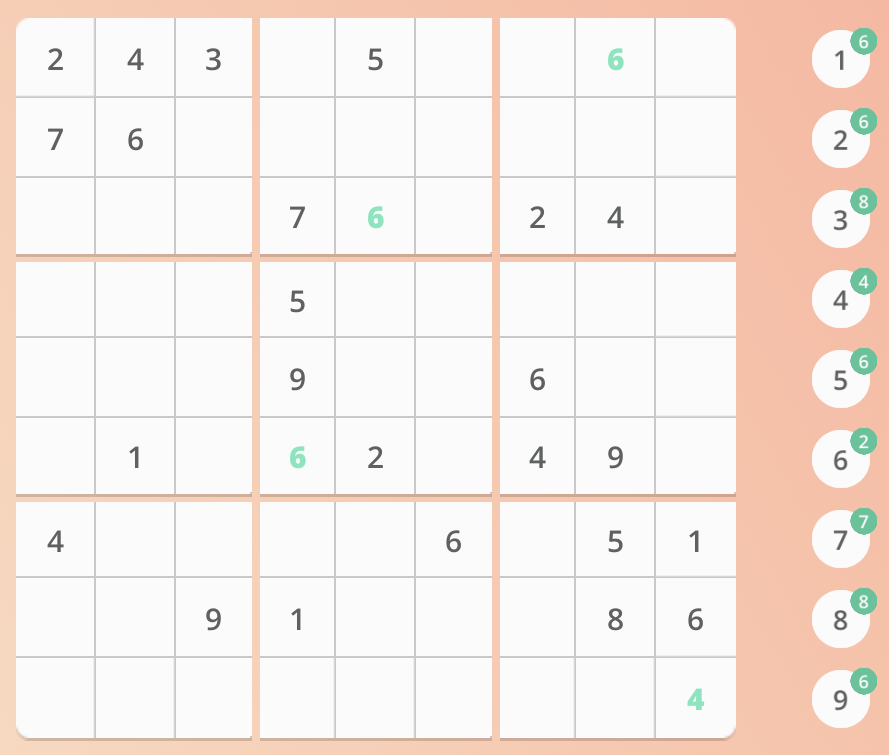
(f). 然后我就发现,做不动了!怎么办呢?我们可以根据 竖列的性质来做,因为每一竖列划分也是不能 同为一值 的。(比如最右方 1 6 4 已经占领了右下九宫格的最后一列,所以我们的 2 只能在前两列出现,但是右上九宫格的 2 出现在了第一列,所以 2 只能在右下九宫格的 (2,3) 位置了)。
(g). 还有呢?我们可以做横列分析这个是比较笨的方法,我能不用就不用!
原理——一个位置可能出现的数值集合 = {1,2,3,4,5,6,7,8,9} - {在这一行出现过的数值} - {在这一列出现过的数值} - {在这一个九宫格出现过的数值},当这个集合只能有 1个数值的时候我们就可以做判断了。
适用范围——当某一行和某一列的出现过的数值集合相差较大时,以及某一个划分已经有8个数值填好了的情况。
举例——上面图中的 8 号位置的 7 号位所在行出现数值集合 = {2,3,4,5,6},列对应集合 = {1,5,6,7,9},所以只能填 8 了。
(h). 那这样就可以了吗?显然不是这样!看下图的提示位置实际上能出现的值里没有 9,为什么呢?因为 1 号位 九宫格的 6 号位是 9 所以 第 3 列是不可能有 9 的,进而确定了 7 号位九宫格的 9 只能出现在 (3,1) 和 (3,2) 位置,也就是说第 3 行,所以自动绑定了 8、9 号位的九宫格内 9 不能出现在 第 3 行!同理,可以得到 9 号位九宫格的 9 只能出现在 第三列。

(i). 特别的还有 多项对应,就是比如 有 3 个位置, 第一个位置可能取值于 {1,2,3}中的一个,而第二第三位置可能取值{2,3}中的一个!那么第一个位置只可能是 1!