1.norm实现数据归一化
import numpy as np
x=np.array([[0, 3, 4], [2, 6, 4]])
y=np.linalg.norm(x, axis=1, keepdims=True)
z=x/y
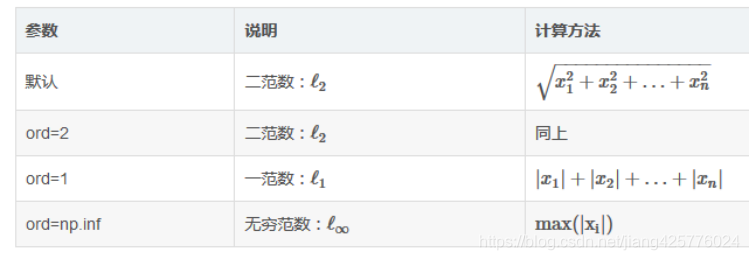
ord : 为设置具体范数值, axis 向量的计算方向。
axis=1表示按行向量处理,求多个行向量的范数
axis=0表示按列向量处理,求多个列向量的范数
axis=None表示矩阵范数。
keepdims:是否保持矩阵的二维特性,True表示保持矩阵的二维特性,False相反
例子:
x = np.array([
[0, 3, 4],
[1, 6, 4]])
#默认参数ord=None,axis=None,keepdims=False
print "默认参数(矩阵整体元素平方和开根号,不保留矩阵二维特性):",np.linalg.norm(x)
print "矩阵整体元素平方和开根号,保留矩阵二维特性:",np.linalg.norm(x,keepdims=True)
print "矩阵每个行向量求向量的2范数:",np.linalg.norm(x,axis=1,keepdims=True)
print "矩阵每个列向量求向量的2范数:",np.linalg.norm(x,axis=0,keepdims=True)
print "矩阵1范数:",np.linalg.norm(x,ord=1,keepdims=True)
print "矩阵2范数:",np.linalg.norm(x,ord=2,keepdims=True)
print "矩阵∞范数:",np.linalg.norm(x,ord=np.inf,keepdims=True)
print "矩阵每个行向量求向量的1范数:",np.linalg.norm(x,ord=1,axis=1,keepdims=True) 
估计线性模型中的系数:a=np.linalg.lstsq(x,b),有b=a*x
求方阵的逆矩阵np.linalg.inv(A)
求广义逆矩阵:np.linalg.pinv(A)
求矩阵的行列式:np.linalg.det(A)
解形如AX=b的线性方程组:np.linalg.solve(A,b)
求矩阵的特征值:np.linalg.eigvals(A)
求特征值和特征向量:np.linalg.eig(A)
Svd分解:np.linalg.svd(A)