利用有限差分法,解矩形波导内场解和截止频率:
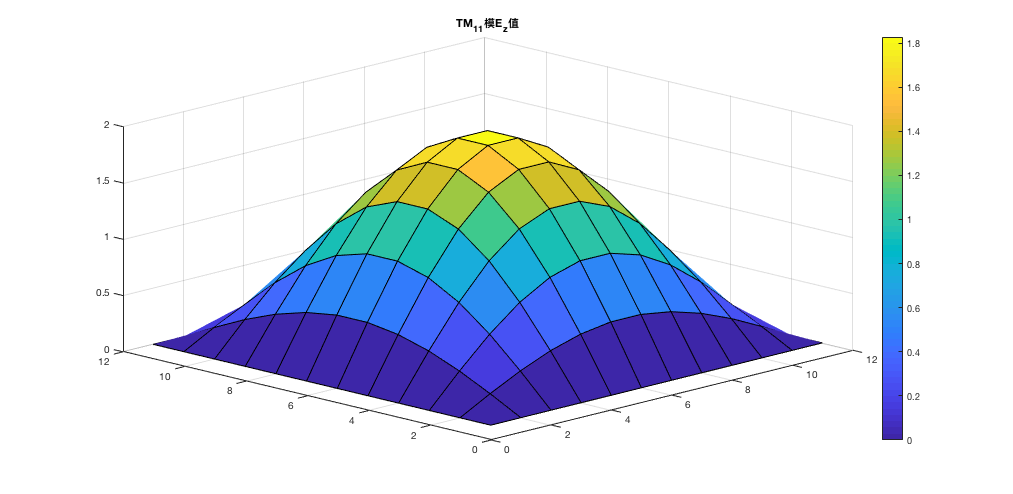
这里以解TM11模为例,利用双重迭代法,每4次场值,更新一次Kc:
%% % 求矩形波导中TM11模 截面内场分布、截止频率kc和特性阻抗Zc % 2018/11/12 % %% Init clear; clc w = 1.5; %收敛因子 count = 20000; %迭代次数 xa = 12; xb = 12; %矩阵长宽度 h = pi / 7; aa = h*(xa-1); bb = h*(xb-1); %% 赋初值 % 内点初值 for i = 2 : (xa-1) for j = 2 : (xb - 1) u(i, j) = 1.15; end end % 边的初值 u(1,:) = 0; u(12,:) = 0; u(:,1) = 0; u(:,12) = 0; % kc初值 kc = 0.15; %% 迭代更新 k = 0; k2 = 0; sum1 = 0; sum2 = 0; sum = 0; while k < count for i = 2 : xa-1 for j = 2 : xb-1 u(i,j) = u(i,j) + w*((u(i+1,j)+u(i,j+1)+u(i-1,j)+u(i,j-1))/(4-(kc*h)^2) -u(i,j)); end end k = k + 1; k2 = k2 + 1; if(rem(k2,3) == 0) for i = 2 : xa-1 for j = 2 : xb-1 sum1 = sum1+ u(i,j)*(u(i+1,j)+u(i,j+1)+u(i-1,j)+u(i,j-1)-4*u(i,j)); sum2 = sum2 + u(i,j)^2; end end kc = sqrt(-sum1/sum2)/h; end end %% 结果展示 surf(u); title('TM_{11}模E_z值'); colorbar c = 3 * 10^8; fc = c * kc /(2*pi*10^6) kc kc0 = sqrt((pi/aa)^2+(pi/bb)^2) max(max(u))
最后效果如图所示: