1、bellman-ford算法

对每条边松弛|V|-1次。

运行结果如下:
(实现的例子)


1 #include<stdio.h> 2 #include<stdlib.h> 3 #define maxnum 100 4 #define maxint 99999 5 6 // 边, 7 typedef struct Edge{ 8 int u, v; // 起点,终点 9 int weight; // 边的权值 10 }Edge; 11 12 Edge edge[maxnum]; // 保存边的值 13 int dist[maxnum]; // 结点到源点最小距离 14 15 int nodenum, edgenum, source; // 结点数,边数,源点 16 17 // 初始化图 18 void init() 19 { 20 // 输入 21 printf("请输入结点数 边数 源点: "); 22 scanf("%d %d %d",&nodenum, &edgenum, &source); 23 for(int i=1; i<=nodenum; ++i) 24 dist[i] = maxint; 25 dist[source] = 0; 26 27 for(int i=1; i<=edgenum; ++i) 28 { 29 scanf("%d %d %d",&edge[i].u, & edge[i].v,&edge[i].weight); 30 if(edge[i].u == source) //注意这里设置初始情况 31 dist[edge[i].v] = edge[i].weight; 32 } 33 } 34 35 // 松弛计算 36 void relax(int u, int v, int weight) 37 { 38 if(dist[v] > dist[u] + weight) 39 dist[v] = dist[u] + weight; 40 } 41 42 bool Bellman_Ford() 43 { 44 for(int i=1; i<=nodenum-1; ++i) 45 for(int j=1; j<=edgenum; ++j) 46 relax(edge[j].u, edge[j].v, edge[j].weight); 47 bool flag = 1; 48 // 判断是否有负环路 49 for(int i=1; i<=edgenum; ++i) 50 if(dist[edge[i].v] > dist[edge[i].u] + edge[i].weight) 51 { 52 flag = 0; 53 printf("有负环路 "); 54 break; 55 } 56 printf("没有负环路 "); 57 return flag; 58 59 } 60 int main() 61 { 62 init(); 63 if(Bellman_Ford()) 64 for(int i = 1 ;i < nodenum; i++) 65 printf("点s->点%d:%d ",i,dist[i]); 66 return 0; 67 }
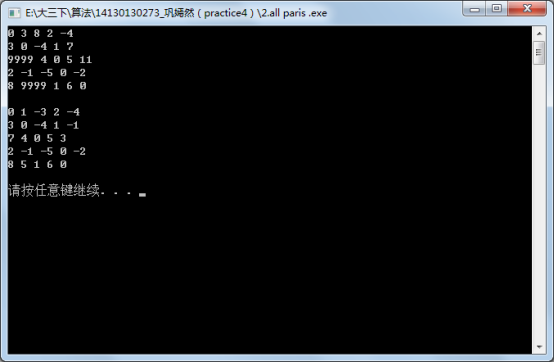
2、All-pairs shortest path (choose one from the three algorithms)


(实现的例子)
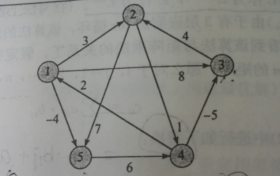
运行结果:
1 #include <cstdlib> 2 #include <iostream> 3 #define N 9999 4 using namespace std; 5 int l[5][5] = {{0, 3, 8, N, -4}, {N, 0, N, 1, 7}, {N, 4, 0, N, N}, {2, N, -5, 0, N}, {N, N, N, 6, 0}}; 6 int w[5][5]; 7 void print() 8 { 9 for(int i = 0; i < 5; i++) 10 { 11 for(int j = 0; j < 5; j++) 12 cout << w[i][j] << " "; 13 cout << endl; 14 } 15 } 16 17 void ExtendShortestPath() 18 { 19 int t; 20 for(int i = 0; i < 5; i++) 21 for(int j = 0; j < 5; j++) 22 { 23 t = N; 24 for(int k = 0; k < 5; k++)//k值代表最多几条路径 25 { 26 27 if(l[i][j] > l[i][k] + l[k][j] && t > l[i][k] + l[k][j]) 28 { 29 w[i][j] = l[i][k] + l[k][j]; 30 t = w[i][j]; 31 } 32 } 33 } 34 } 35 36 int main(int argc, char *argv[]) 37 { 38 for(int i = 0; i < 5; i++) 39 { 40 for(int j = 0; j < 5; j++) 41 { 42 w[i][j] = l[i][j]; 43 } 44 } 45 int m; 46 m = 1; 47 while(m < 4) 48 { 49 ExtendShortestPath(); 50 m*=2; 51 print(); 52 for(int i = 0; i <5; i++) 53 { 54 for(int j = 0; j < 5; j++) 55 { 56 l[i][j] = w[i][j]; 57 } 58 } 59 cout << endl; 60 } 61 62 system("PAUSE"); 63 return 0; 64 }
3、8-queen problem (back backing)


运行结果如下:

1 #include <stdio.h> 2 #include <stdlib.h> 3 4 #define max 8 5 6 7 int queen[max], sum=0; /* max为棋盘最大坐标 */ 8 9 void show() /* 输出所有皇后的坐标 */ 10 { 11 int i; 12 for(i = 0; i < max; i++) 13 { 14 printf("(%d,%d) ", i, queen[i]); 15 } 16 printf(" "); 17 sum++; 18 } 19 20 int check(int n) /* 检查当前列能否放置皇后 */ 21 { 22 int i; 23 for(i = 0; i < n; i++) /* 检查横排和对角线上是否可以放置皇后 */ 24 { 25 if(queen[i] == queen[n] || abs(queen[i] - queen[n]) == (n - i)) 26 { 27 return 1; 28 } 29 } 30 return 0; 31 } 32 33 void put(int n) /* 回溯尝试皇后位置,n为横坐标 */ 34 { 35 int i; 36 for(i = 0; i < max; i++) 37 { 38 queen[n] = i; /* 将皇后摆到当前循环到的位置 */ 39 if(!check(n)) 40 { 41 if(n == max - 1) 42 { 43 show(); /* 如果全部摆好,则输出所有皇后的坐标 */ 44 } 45 else 46 { 47 put(n + 1); /* 否则继续摆放下一个皇后 */ 48 } 49 } 50 } 51 } 52 53 int main() 54 { 55 put(0); /* 从横坐标为0开始依次尝试 */ 56 printf(" 总方法数:%d", sum); 57 system("pause"); 58 return 0; 59 }
4、0-1 knapsack problem (back tracking)

对一组数据,有两种可能:选或不选,在树种用左右字数表示。
使用递归,在遍历完n个数时,判断最终的数是否比最佳价值大,如比最佳大,则把值付给besrv。

上界函数:当前的价值cw+剩余可容纳的最大价值<=当前最优解

运行结果如下:
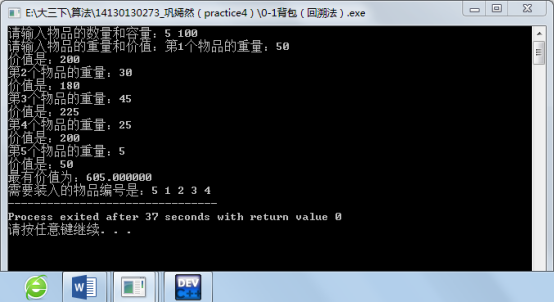
1 #include <stdio.h> 2 #include <conio.h> 3 4 int n;//物品数量 5 double c;//背包容量 6 double v[100];//各个物品的价值 7 double w[100];//各个物品的重量 8 double cw = 0.0;//当前背包重量 9 double cp = 0.0;//当前背包中物品价值 10 double bestp = 0.0;//当前最优价值 11 double perp[100];//单位物品价值排序后 12 int order[100];//物品编号 13 int put[100];//设置是否装入 14 15 //计算上界函数 16 double bound(int i) 17 { 18 double leftw= c-cw; 19 double b = cp; 20 while(i<=n&&w[i]<=leftw) 21 { 22 leftw-=w[i]; 23 b+=v[i]; 24 i++; 25 } 26 if(i<=n) 27 b+=v[i]/w[i]*leftw; 28 return b; 29 } 30 31 //按单位价值排序 32 void knapsack() 33 { 34 int i,j; 35 int temporder = 0; 36 double temp = 0.0; 37 for(i=1;i<=n;i++ ) 38 perp[i]=v[i]/w[i]; 39 for(i=1;i<=n-1;i++) 40 { 41 for(j=i+1;j<=n;j++) 42 if(perp[i]<perp[j]) 43 { 44 temp = perp[i]; 45 perp[i]=perp[i]; 46 perp[j]=temp; 47 temporder=order[i]; 48 order[i]=order[j]; 49 order[j]=temporder; 50 temp = v[i]; 51 v[i]=v[j]; 52 v[j]=temp; 53 temp=w[i]; 54 w[i]=w[j]; 55 w[j]=temp; 56 } 57 } 58 } 59 60 //回溯函数 61 void backtrack(int i) 62 { 63 double bound(int i); 64 if(i>n) 65 { 66 bestp = cp; 67 return; 68 } 69 if(cw+w[i]<=c) 70 { 71 cw+=w[i]; 72 cp+=v[i]; 73 put[i]=1; 74 backtrack(i+1); 75 cw-=w[i]; 76 cp-=v[i]; 77 } 78 if(bound(i+1)>bestp)//符合条件搜索右子数 79 backtrack(i+1); 80 } 81 82 int main() 83 { 84 int i; 85 printf("请输入物品的数量和容量:"); 86 scanf("%d %lf",&n,&c); 87 printf("请输入物品的重量和价值:"); 88 for(i=1;i<=n;i++) 89 { 90 printf("第%d个物品的重量和价值:",i); 91 scanf("%lf",&w[i],&v[i]); 92 printf("第%d个物品的价值:",i); 93 scanf("%lf",&v[i]); 94 order[i]=i; 95 } 96 knapsack(); 97 backtrack(1); 98 printf("最有价值为:%lf ",bestp); 99 printf("需要装入的物品编号是:"); 100 for(i=1;i<=n;i++) 101 { 102 if(put[i]==1) 103 printf("%d ",order[i]); 104 } 105 return 0; 106 }