1. Matrix-chain product. The following are some instances
a) <3, 5, 2, 1,10>
b) <2, 7, 3, 6, 10>
c) <10, 3, 15, 12, 7, 2>
d) <7, 2, 4, 15, 20, 5>
算法: 0 (i=j时)
m[i,j]=
Min{ m[i,k]+m[k+1,j]+pi-1pkpl} (i<j时)
用s[i,j]表示m[i,j]最小时的k值,备忘录是n*n的m[i,j]和s[i,j]。

定义表m和表s为全局变量,m[i][j]的值是子问题最优解的代价,s[i][j]的值是最优方案的分割点k。
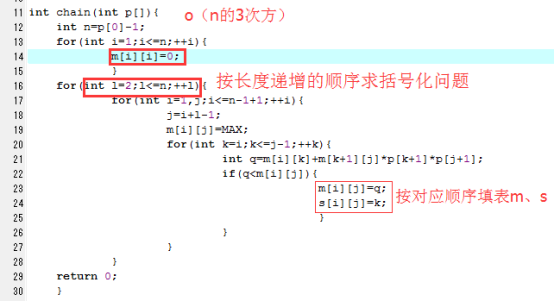
利用自底向上表格法。在每步循环中,计算代价m依赖于已经计算出的表项m[i][k]和m[k+1][j]。算法运行时间为o(n的3次方),还要c塔(n平方)的内存空间保存表m、s。

我不会给c语言的函数传入二维数组,所以同样的算法用java来做运行结果图在最后。
递归输出最优方案。

在java中运行同样的算法结果 如下:

public class ex1 { public static void chain(int[] A) { int n = A.length; int[][] m = new int[n][n]; int[][] s = new int[n][n]; for (int i = 1; i < n; i++) { m[i][i] = 0; } for (int l = 2; l < n; l++) { for (int i = 1; i < n - l + 1; i++) { int j = i + l - 1; m[i][j] = Integer.MAX_VALUE; for (int k = i; k <= j - 1; k++) { int q = m[i][k] + m[k + 1][j] + A[i - 1] * A[k] * A[j]; if (q < m[i][j]) { m[i][j] = q; s[i][j] = k; } } } } System.out.println("最小乘法次数"+m[1][n-1]); PrintOptimalParens(s,1,n-1); } public static void PrintOptimalParens(int[][] s, int i, int j) { if (i == j) { System.out.print("A"+i); } else { System.out.print("("); PrintOptimalParens(s,i,s[i][j]); PrintOptimalParens(s,s[i][j]+1,j); System.out.print(")"); } } public static void main(String[] args) { int[] A = {3,5,2,1,10}; int[] B = {2,7,3,6,10}; int[] C = {10, 3, 15, 12, 7, 2}; int[] D = {7, 2, 4, 15, 20, 5}; chain(A); System.out.println(); chain(B); System.out.println(); chain(C); System.out.println(); chain(D); System.out.println(); } }
2. Longest Common Subsequence (LCS). The following are some instances.
a) X: xzyzzyx Y: zxyyzxz
b) X: ALLAAQANKESSSESFISRLLAIVAD
Y: KLQKKLAETEKRCTLLAAQANKENSNESFISRLLAIVAG
算法: c[i-1 , j -1]+1 (i , j >0 ,xi等于 yi)
c[i,j]=
Max{ c[I , j -1], c[i-1 , j ]} (i , j >0 ,xi不等于 yi)
B【i,j】为标记函数,若c[i,j]规约为c[i-1,j-1],则为“X”;
若c[i,j]规约为c[i-1,j],则为“U”
若c[i,j]规约为c[i,j-1],则为 “L”
程序运行结果图如下:
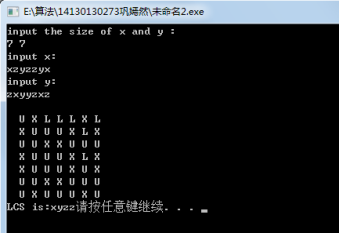
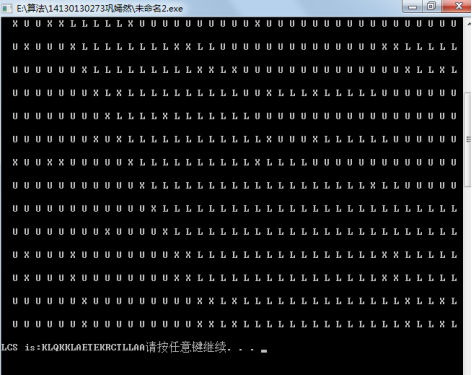

把待求的字符数组定义为全局变量,表c[i][j]表示xi和yj的长度,表b[i][j]是计算c[i][j]时所选择的子问题的最优解。



#include<stdio.h> #include<stdlib.h> #include<string.h> //第一题 char x[]="xzyzzyx"; char y[]="zxyyzxz"; int xlen=strlen(x); int ylen=strlen(y); int c[100][100]; char b[100][100]; int LEN(){ int m=xlen; int n=ylen; for(int i=0;i<m;++i){ c[i][0]=0; } for(int j=0;j<n;++j){ c[0][j]=0; } for(int i=1;i<=m;++i){ for(int j=1;j<=n;++j){ if(x[i]==y[j]){ c[i][j]=c[i-1][j-1]+1; b[i][j]='X'; } else if(c[i-1][j]>=c[i][j-1]){ c[i][j]=c[i-1][j]; b[i][j]='U'; } else{ c[i][j]=c[i][j-1]; b[i][j]='L'; } } } return 0; } int print(int i,int j){ if(i==0||j==0){ return 0; } if(b[i][j]=='X'){ print(i-1,j-1); printf("%c",x[i]); } else if(b[i][j]=='U'){ print(i-1,j); } else print(i,j-1); return 0; } int main(){ printf("input the size of x and y : "); scanf("%d%d",&xlen,&ylen); printf("input x: "); fflush(stdin); for(int i = 1;i<=xlen;++i){ scanf("%c",&x[i]); } printf("input y: "); fflush(stdin); for(int i = 1;i<=ylen;++i){ scanf("%c",&y[i]); } LEN(); for(int i=0;i<=xlen;i++){ for(int j=0;j<=ylen;j++){ printf("%d%c ",c[i][j],b[i][j]); } printf(" "); } printf("LCS is:"); print(xlen,ylen); system("pause"); return 0; }
3. Max Sum. The following are some instances:
a) (-2,11,-4,13,-5,-2)


B数组记录了以当前元素为结尾时,最大字段的和,用第一个循环完成。
第二个循环,打印B数组。
第三个循环,遍历B数组,找到最大值。
1 #include<stdio.h> 2 #include<stdlib.h> 3 #define N 10 4 int maxsum(int a[],int n) 5 { 6 int sum = 0; 7 int b[N]; 8 b[0] = a[0]; 9 for(int i = 1; i < n; i++) 10 { 11 if(b[i-1] > 0) 12 b[i] = b[i - 1] + a[i]; 13 else 14 b[i] = a[i]; 15 } 16 printf("当前的B数组为:"); 17 for(int i=0;i<6;i++){ 18 printf("%d ",b[i]); 19 } 20 for(int j = 0; j < n; j++) 21 { 22 if(b[j] > sum) 23 sum = b[j]; 24 } 25 return sum; 26 } 27 int main(){ 28 int a[7]={-2,11,-4,13,-5,-2}; 29 printf(" 最大子段和是:%d ",maxsum(a,6)); 30 system("pause"); 31 return 0; 32 }
4. (Optional) Shortest path in multistage graphs. Find the shortest path from 0 to 15 for the following graph.
A multistage graph is a graph (1) G=(V,E) with V partitioned into K >= 2 disjoint subsets such that if (a,b) is in E, then a is in Vi , and b is in Vi+1 for some subsets in the partition; and (2) | V1 | = | VK | = 1.
5. (Optional) Longest Common Substring. The following are some instances.
a) X: xzyzzyx Y: zxyyzxz
b) X:MAEEEVAKLEKHLMLLRQEYVKLQKKLAETEKRCALLAAQANKESSSESFISRLLAIVAD
Y:MAEEEVAKLEKHLMLLRQEYVKLQKKLAETEKRCTLLAAQANKENSNESFISRLLAIVAG

这个题是算子串(必须连续),代码和第二题算子序列(可以不连续)很相似。此题值考虑i==j的情况
其余代码与第二题一致。