P5030 长脖子鹿放置 最小割

$ color{#0066ff}{ 题目描述 }$

如图所示，西洋棋的“长脖子鹿”，类似于中国象棋的马，但按照“目”字攻击，且没有中国象棋“别马腿”的规则。（因为长脖子鹿没有马腿）

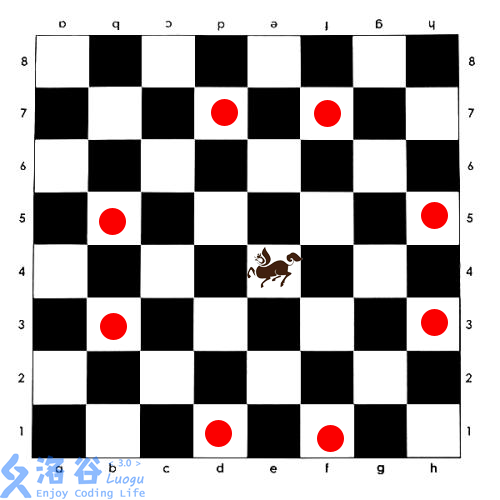
给定一个(N * M),的棋盘，有一些格子禁止放棋子。问棋盘上最多能放多少个不能互相攻击的长脖子鹿。

(color{#0066ff}{输入格式})

输入的第一行为两个正整数(N)，(M)，(K)。其中(K)表示禁止放置长脖子鹿的格子数。

第(2)~第(K+1)行每一行为两个整数(Xi, Yi),表示禁止放置的格子。

(color{#0066ff}{输出格式})

一行一个正整数，表示最多能放置的长脖子鹿个数。

(color{#0066ff}{输入样例})

8 7 5
1 1
5 4
2 3
4 7
8 3
    
    
2 2 1
1 1

(color{#0066ff}{输出样例})

28
    
3

(color{#0066ff}{数据范围与提示})

重要提示：请务必思考对图的遍历顺序对运行速度的影响

对于(10\%)的数据， (1 ≤ N,M ≤ 5)

对于(30\%)的数据， (1 ≤ N,M ≤ 10)

对于(60\%)的数据， (1 ≤ N,M ≤ 50)

对于(80\%)的数据， (1 ≤ N,M ≤ 100)

对于(100\%)的数据，(1 ≤ N,M ≤ 200)

(color{#0066ff}{题解})

然而，并不能黑白染色（由图显然）

但是。。。TM可以对行号的奇偶进行染色！

于是按行奇偶黑白染色，跑最小割就行了

// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define LL long long
LL read() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
template<class T> bool chkmax(T &a, const T &b) { return a < b? a = b, 1 : 0; }
template<class T> bool chkmin(T &a, const T &b) { return b < a? a = b, 1 : 0; }
const int inf = 0x7fffffff;
const int maxn = 1e5 + 10;
struct node {
	int to, can;
	node *nxt, *rev;
	node(int to = 0, int can = 0, node *nxt = NULL): to(to), can(can), nxt(nxt) { rev = NULL; }
};
node *head[maxn], *cur[maxn];
int dep[maxn], n, s, t, mp[400][400], m, num;
int rx[] = {-3, -3, -1, -1, 1, 1, 3, 3};
int ry[] = {-1, 1, 3, -3, 3, -3, -1, 1};
bool bfs() {
	for(int i = s; i <= t; i++) dep[i] = 0, cur[i] = head[i];
	std::queue<int> q;
	q.push(s); dep[s] = 1;
	while(!q.empty()) {
		int tp = q.front(); q.pop();
		for(node *i = head[tp]; i; i = i->nxt) 
			if(!dep[i->to] && i->can)
				dep[i->to] = dep[tp] + 1, q.push(i->to);
	}
	return dep[t];
}
int dfs(int x, int change) {
	if(x == t || !change) return change;
	int flow = 0, ls;
	for(node *&i = cur[x]; i; i = i->nxt)
		if(dep[i->to] == dep[x] + 1 && (ls = dfs(i->to, std::min(change, i->can)))) {
			change -= ls;
			flow += ls;
			i->can -= ls;
			i->rev->can += ls;
			if(!change) break;
		}
	return flow;
}
int dinic() {
	int flow = 0;
	while(bfs()) flow += dfs(s, inf);
	return flow;
}
int id(int x, int y) { return (x - 1) * m + y; }
void add(int from, int to, int can) { head[from] = new node(to, can, head[from]); }
void link(int from, int to, int can) {
	add(from, to, can), add(to, from, 0);
	head[from]->rev = head[to]; head[to]->rev = head[from];
}
int main() {
	n = read(), m = read(), num = read();
	int x, y;
	for(int i = 1; i <= num; i++) x = read(), y = read(), mp[x][y] = true;
	num = n * m - num;
	s = 0, t = n * m + 1;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) {
			if(mp[i][j]) continue;
			if(i & 1) link(id(i, j), t, 1);
			else link(s, id(i, j), 1);
			if(i & 1) continue;
			for(int k = 0; k < 8; k++) {
				int xx = i + rx[k];
				int yy = j + ry[k];
				if(xx >= 1 && xx <= n && yy >= 1 && yy <= n && !mp[xx][yy])  link(id(i, j), id(xx, yy), inf);
			}
		}
	}
	printf("%d
", num - dinic());
	return 0;
}