LCT
LCT 即 Link-Cut-Tree
维护一个森林, 支持很多操作,比如:
-
维护链上信息(min,max,sum,xor。。。。。。)
-
换根
-
动态维护联通性
-
维护子树信息
概念
虚边:连接儿子与父亲,儿子记录父亲,父亲不记录儿子(父不认子)
实边:父子互认,互相记录
每棵树维护多棵splay(常数大。。。QAQ)
性质
-
每一个splay维护从上到下按在原树中的深度严格递增的路径,且中序遍历splay得到的每个点的深度序列严格递增
-
每个节点包含且仅包含于一个splay中
-
实边在splay中,由一棵Splay指向另一Splay的边为虚边 (这条边是该splay中中序遍历最靠前的点和其原树中父亲相连的边)
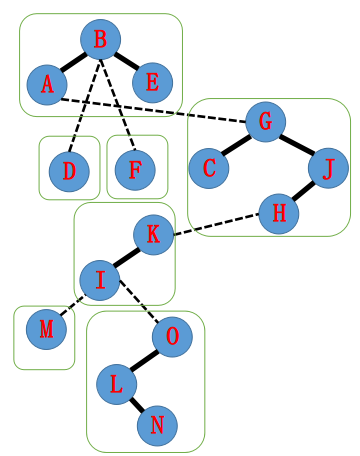
绿框中的为一个splay里面都是实边
连接两个splay的是虚边
注意,虚边中父亲不认孩子
-
某个点有多个儿子,只能认一个儿子拉入Splay中
其它不行!(splay深度严格递增) 其它儿子父亲不认(虚边)
由儿子所属的Splay的根的父节点指向该点,且父不认子。。。
一些操作
-
access(基础)
作用:打通根到某一节点的实链,放在同一splay中,且此节点的深度最深!
方式:虚边变实边,然后为了维护性质,原来实边变为虚边, 由根到此节点的路径上全为实边, 而且由于它是最深的,他下面都是虚的!!
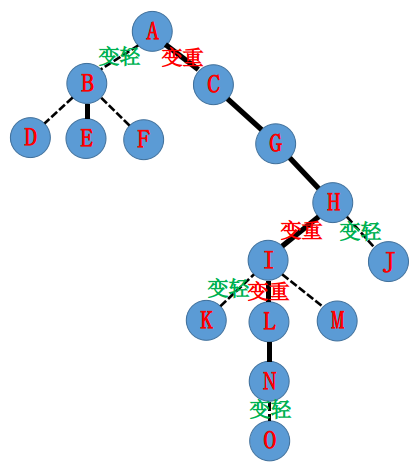 **
**
实现:
void access(node *x) {
for(node *y = NULL; x; x = (y = x)->fa) //无论实边虚边,x都记录了父亲,所以可以一直跳到根
splay(x), x->ch[1] = y, x->upd(); //把x转上来,虚实变换,然后维护信息
}
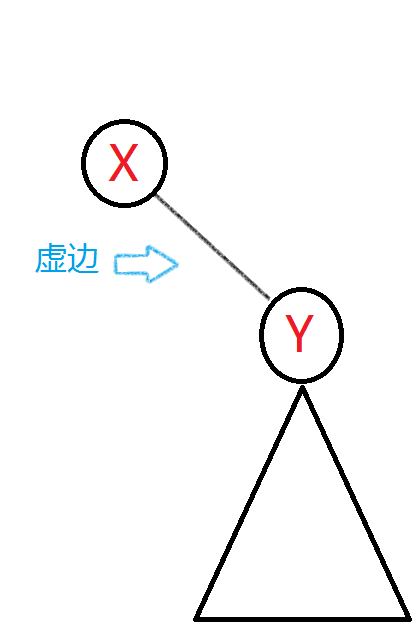
由于深度关系,y一定在x右边,然后让x认亲(虚变实),同时原来的实边不存在了
因为x重新认亲了,之后x继续向上。。。。。。
-
makeroot
作用:将x转变为他所在子树的根
方式:access开路(将其与根放在同一splay上)
splay它,把它转上去,然后翻转左右儿子!
为什么要翻转呢??解释一下
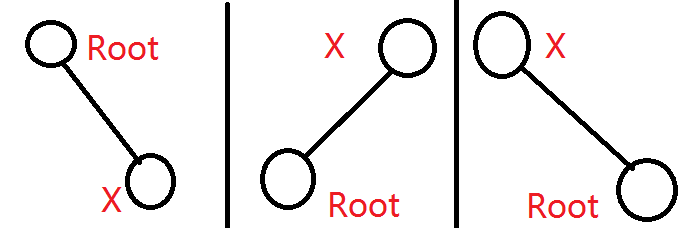
上面分别为(splay前,splay后,翻转后)
splay后,x已经成为了根,所以深度浅于原根,很明显此时不满足性质,所以翻转左右儿子!
-
split(x,y)
作用:琛出一条(x o y)的路径
void split(node *x, node *y) {
makeroot(x); //让x城成为根
access(y); //打通y到根x的路径,那么现在x->y的路径就在一棵Splay里了
splay(y); //转上y更新信息
}
-
findroot(x)
作用:返回x所在树的根(动态判断图的联通性)
方式:access(x),splay(x) 打通x与根的路并转上去,让x一直往左跳并下放翻转标记
看上图splay前和splay后,转后x到了根的位置,但并不是我们所求的根
实际的根由于转前深度最浅到了左儿子处,因此一直往左找就一定是根
-
link(x,y)
作用:连接x,y
方式:把x转成根,直接连
void link(node *x, node *y) {
makeroot(x); //x成为根
if(findroot(y) != x) x->fa = y; //如果根不是x,说明不在一棵树里,否则直接连虚边
}
-
cut(x,y)
作用:断掉x与y的边(前提是有边。。。)
实现:直接打通(x o y)的路径,然后断边就行,前提是数据合法。。。
void cut(node *x, node *y) {
split(x, y);
if(y->ch[0] == x) y->ch[0] = x->fa = NULL;
}
2019.1.11upd
摒弃原来丑陋代码
换上清真的
#include<bits/stdc++.h>
using namespace std;
#define LL long long
LL in() {
char ch; int x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
const int maxn = 3e5 + 5;
struct LCT {
protected:
struct node {
node *ch[2], *fa;
int val, num, rev;
node(int val = 0, int num = 0, int rev = 0): val(val), num(num), rev(rev) {
ch[0] = ch[1] = fa = NULL;
}
bool ntr() { return fa && (fa->ch[0] == this || fa->ch[1] == this); }
bool isr() { return this == fa->ch[1]; }
void trn() { std::swap(ch[0], ch[1]), rev ^= 1; }
void upd() {
num = val;
if(ch[0]) num ^= ch[0]->num;
if(ch[1]) num ^= ch[1]->num;
}
void dwn() {
if(!rev) return;
if(ch[0]) ch[0]->trn();
if(ch[1]) ch[1]->trn();
rev = 0;
}
};
node s[maxn], *t[maxn];
int top;
void rot(node *x) {
node *y = x->fa, *z = y->fa;
int k = x->isr(); node *w = x->ch[!k];
if(y->ntr()) z->ch[y->isr()] = x;
x->ch[!k] = y, y->ch[k] = w;
y->fa = x, x->fa = z;
if(w) w->fa = y;
y->upd(), x->upd();
}
void splay(node *o) {
t[top = 1] = o;
while(t[top]->ntr()) t[top + 1] = t[top]->fa, top++;
while(top) t[top--]->dwn();
while(o->ntr()) {
if(o->fa->ntr()) rot(o->isr() ^ o->fa->isr()? o : o->fa);
rot(o);
}
}
void access(node *x) {
for(node *y = NULL; x; x = (y = x)->fa)
splay(x), x->ch[1] = y, x->upd();
}
void makeroot(node *x) { access(x), splay(x), x->trn(); }
node *findroot(node *x) {
access(x), splay(x);
while(x->dwn(), x->ch[0]) x = x->ch[0];
return x;
}
void link(node *x, node *y) {
if(findroot(x) == findroot(y)) return;
makeroot(x), x->fa = y;
}
void cut(node *x, node *y) {
makeroot(x), access(y), splay(y);
if(y->ch[0] == x) y->ch[0] = x->fa = NULL;
}
void change(node *x, int y) { splay(x), x->val = y, x->upd(); }
int query(node *x, node *y) {
makeroot(x), access(y), splay(y);
return y->num;
}
public:
void init(int len) { for(int i = 1; i <= len; i++) s[i].val = s[i].num = in(); }
int query(int x, int y) { return query(s + x, s + y); }
void link(int x, int y) { link(s + x, s + y); }
void cut(int x, int y) { cut(s + x, s + y); }
void change(int x, int y) { change(s + x, y); }
}s;
int n, m;
int main() {
n = in(), m = in();
s.init(n);
while(m --> 0) {
int flag = in(), x = in(), y = in();
if(flag == 0) printf("%d
", s.query(x, y));
if(flag == 1) s.link(x, y);
if(flag == 2) s.cut(x, y);
if(flag == 3) s.change(x, y);
}
return 0;
}