(color{#0066ff}{ 题目描述 })
Kiana 最近喜欢到一家非常美味的寿司餐厅用餐。
每天晚上,这家餐厅都会按顺序提供 (n) 种寿司,第 (i) 种寿司有一个代号 (a_i) 和美味度 (d_{i, i}) ,不同种类的寿司有可能使用相同的代号。每种寿司的份数都是无限的,(Kiana) 也可以无限次取寿司来吃,但每种寿司每次只能取一份,且每次取走的寿司必须是按餐厅提供寿司的顺序连续的一段,即 (Kiana) 可以一次取走第 (1, 2) 种寿司各一份,也可以一次取走第 (2, 3) 种寿司各一份,但不可以一次取走第 (1, 3) 种寿司。
由于餐厅提供的寿司种类繁多,而不同种类的寿司之间相互会有影响:三文鱼寿司和鱿鱼寿司一起吃或许会很棒,但和水果寿司一起吃就可能会肚子痛。因此,(Kiana) 定义了一个综合美味度 (d_{i, j} (i < j)),表示在一次取的寿司中,如果包含了餐厅提供的从第 (i) 份到第 (j) 份的所有寿司,吃掉这次取的所有寿司后将获得的额外美味度。由于取寿司需要花费一些时间,所以我们认为分两次取来的寿司之间相互不会影响。注意在吃一次取的寿司时,不止一个综合美味度会被累加,比如若 (Kiana) 一次取走了第 (1, 2, 3) 种寿司各一份,除了 (d_{1, 3}) 以外,(d_{1, 2}, d_{2, 3}) 也会被累加进总美味度中。
神奇的是,(Kiana) 的美食评判标准是有记忆性的,无论是单种寿司的美味度,还是多种寿司组合起来的综合美味度,在计入 (Kiana) 的总美味度时都只会被累加一次。比如,若 (Kiana) 某一次取走了第 (1, 2) 种寿司各一份,另一次取走了第 (2, 3)种寿司各一份,那么这两次取寿司的总美味度为 (d_{1, 1} + d_{2, 2} + d_{3, 3} + d_{1, 2} + d_{2, 3}),其中 (d_{2, 2}) 只会计算一次。
奇怪的是,这家寿司餐厅的收费标准很不同寻常。具体来说,如果 (Kiana) 一共吃过了 (c (c > 0)) 种代号为 (x) 的寿司,则她需要为这些寿司付出 (mx^2 + cx) 元钱,其中 (m) 是餐厅给出的一个常数。
现在 (Kiana) 想知道,在这家餐厅吃寿司,自己能获得的总美味度(包括所有吃掉的单种寿司的美味度和所有被累加的综合美味度)减去花费的总钱数的最大值是多少。由于她不会算,所以希望由你告诉她。
(color{#0066ff}{输入格式})
第一行包含两个正整数 (n, m),分别表示这家餐厅提供的寿司总数和计算寿司价格中使用的常数。 第二行包含 (n) 个正整数,其中第 (k) 个数 (a_k) 表示第 (k) 份寿司的代号。 接下来 (n) 行,第 (i) 行包含 (n - i + 1) 个整数,其中第 (j) 个数 (d_{i, i+j-1}) 表示吃掉寿司能获得的相应的美味度,具体含义见问题描述。
(color{#0066ff}{输出格式})
输出共一行包含一个正整数,表示 (Kiana) 能获得的总美味度减去花费的总钱数的最大值。
(color{#0066ff}{输入样例})
10 1
5 5 4 4 1 2 5 1 5 3
83 91 72 29 22 -5 57 -14 -36 -3
-11 34 45 96 32 73 -1 0 29
-48 68 44 -5 96 66 17 74
88 47 69 -9 2 25 -49
86 -9 -77 62 -10 -30
2 40 95 -74 46
49 -52 2 -51
-55 50 -44
72 22
-68
(color{#0066ff}{输出样例})
1223
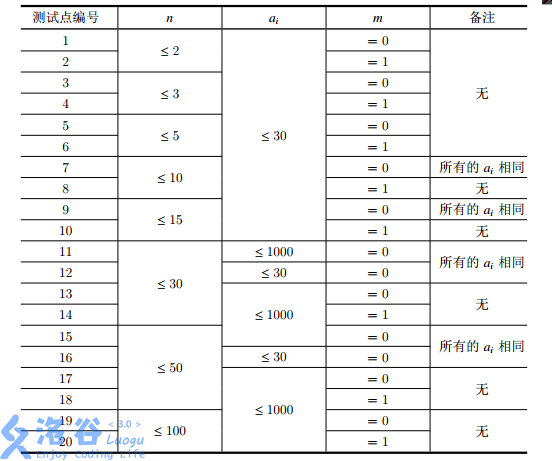
(color{#0066ff}{数据范围与提示})
(color{#0066ff}{题解})
这是一个最大流最小割的题
要找最大的美味度-花费
我们找到总美味度,用最小割求花费,一减就行了
首先考虑总美味度的问题
因为有负的美味度
考虑将其算在花费里就行了,因为我们并不知道总美味度里到底包不包括某些负的值
将其算作花费在网络流上跑,这样才能保证最大
下面开始花式建边
建边
1、原点向每个美味度为正的区间连容量为美味度的边
2、每个美味度为负的区间像汇点连容量为-美味度的边
3、每个区间([i,j])向区间([i+1,j], [i,j-1])连一条容量为inf的边
4、每个区间向区间端点对应的寿司连一条inf的边
5、每个寿司向汇点连容量为寿司种类编号的边
6、每个寿司向所属寿司种类连容量为inf的边
7、每个寿司种类向汇点连容量为(m * id * id)的边
#include<bits/stdc++.h>
#define LL long long
LL in() {
char ch; int x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
struct node {
int to, dis;
node *nxt, *rev;
node(int to = 0, int dis = 0, node *nxt = NULL): to(to), dis(dis), nxt(nxt) {}
void *operator new (size_t) {
static node *S = NULL, *T = NULL;
return (S == T) && (T = (S = new node[1024]) + 1024), S++;
}
};
const int maxn = 10505;
const int mod = 150;
const int inf = 0x7fffffff;
int id[mod][mod], val[mod][mod], idd[maxn];
int dep[maxn], a[mod];
node *head[maxn], *cur[maxn];
int n, s, t, m;
int ans;
using std::queue;
queue<int> q;
void add(int from, int to, int dis) {
head[from] = new node(to, dis, head[from]);
}
void link(int from, int to, int dis) {
add(from, to, dis);
add(to, from, 0);
head[from]->rev = head[to];
head[to]->rev = head[from];
}
bool bfs() {
for(int i = s; i <= t; i++) cur[i] = head[i], dep[i] = 0;
q.push(s);
dep[s] = 1;
while(!q.empty()) {
int tp = q.front(); q.pop();
for(node *i = head[tp]; i; i = i->nxt)
if(!dep[i->to] && i->dis) {
dep[i->to] = dep[tp] + 1;
q.push(i->to);
}
}
return dep[t];
}
int dfs(int x, int change) {
if(x == t || !change) return change;
int flow = 0, ls;
for(node *i = cur[x]; i; i = i->nxt) {
cur[x] = i;
if(dep[i->to] == dep[x] + 1 && (ls = dfs(i->to, std::min(change, i->dis)))) {
flow += ls;
change -= ls;
i->dis -= ls;
i->rev->dis += ls;
if(!change) break;
}
}
return flow;
}
int dinic() {
int flow = 0;
while(bfs()) flow += dfs(s, inf);
return flow;
}
void build() {
int cnt = 0;
for(int i = 1; i <= n; i++)
for(int j = i; j <= n; j++)
id[i][j] = ++cnt;
static bool vis[maxn];
for(int i = 1; i <= n; i++)
if(!vis[a[i]]) {
vis[a[i]] = true;
idd[a[i]] = ++cnt;
}
memset(vis, 0, sizeof vis);
s = 0, t = cnt + n + 1;
for(int i = 1; i <= n; i++)
if(!vis[a[i]]) {
vis[a[i]] = true;
link(idd[a[i]], t, m * a[i] * a[i]);
}
for(int i = 1; i <= n; i++) {
link(cnt + i, idd[a[i]], inf);
link(cnt + i, t, a[i]);
}
for(int i = 1; i <= n; i++)
for(int j = i; j <= n; j++) {
if(val[i][j] >= 0) {
ans += val[i][j];
link(s, id[i][j], val[i][j]);
link(id[i][j], cnt + i, inf);
link(id[i][j], cnt + j, inf);
}
else {
link(id[i][j], t, -val[i][j]);
link(id[i][j], cnt + i, inf);
link(id[i][j], cnt + j, inf);
}
if(i != j) {
link(id[i][j], id[i + 1][j], inf);
link(id[i][j], id[i][j - 1], inf);
}
}
}
int main() {
n = in(), m = in();
for(int i = 1; i <= n; i++) a[i] = in();
for(int i = 1; i <= n; i++)
for(int j = i; j <= n; j++)
val[i][j] = in();
build();
printf("%d", ans - dinic());
return 0;
}