• 遗传算法解决寻路问题——Python描述

    概要

    我的上一篇写遗传算法解决排序问题，当中思想借鉴了遗传算法解决TSP问题，本质上可以认为这是一类问题，就是这样认为：寻找到一个序列X，使F（X）最大。

    详解介绍

    排序问题：寻找一个序列，使得这个序列的逆序对的倒数最大。

    TSP问题：寻找一个序列，使得这个序列的总路径长的倒数最大。

    这两个问题有一个共同的特点是，所有的节点都要用上，而使用遗传算法解决排序问题（每一个格子可以认为是一个节点），是需要从众多的节点之中寻找到某些节点构成一个序列X。

    序列X必须满足的条件是：

    1. 相邻节点直接邻接
    2. 无重复节点（有重复的相当于走回头路）
    3. 序列的起点和终点必须是已知的点

    第一个需要解决的问题是初代如何选择：

    1. 随机选择然后判断是否符合上面的三个条件（垃圾）
    2. 从起点开始随机生成到终点的序列

    第二种做法的另一个问题就是随机性太大，可能会走比较长的路（其实也是可以采用的），为了解决这个问题，我才用了A*算法的启发式思维，将当前点和目标点的蔓哈顿距离作为适应度加入到优先队列中。

     

    算法步骤

    1. 将起点加入到优先队列中
    2. 从优先队列中取出顶部顶点p0，将p0加入到Path(路径结果),如果p0是终点结束；
    3. 随机获取其周围的8个点中的一个p1
    4. 比较p0到目标点的曼哈顿距离|p0-target|  和p1到目标点的距离|p1-target|
    5. 如果|p1-target|<|p0-target|并且p1 not in Path, 将p1加入优先队列，p0<-p1；转到2

    使用这种策略不仅引入了随机性，而且路径也比较合适，收敛比较快。

    选择

    这一步比较简单，就是普通的轮盘法就ok

    交叉和变异

    目前还没有想到策略（后面补充）

    代码实现

      1 import random
  2 import math
  3 import copy
  4 from tkinter import *
  5 import tkinter.font as tkFont
  6 import time, threading
  7 
  8 WIDTH = 100
  9 HEIGHT = 100
 10 MIN = 0
 11 MAX = WIDTH * HEIGHT - 1
 12 
 13 PATH_COUNT = 100
 14 # 交叉概率
 15 cross_p = 0.6
 16 # 变异概率
 17 variation_p = 0.4
 18 # 变异次数
 19 variation_times = 4
 20 
 21 DIS_1 = 1.4
 22 DIS_2 = 1
 23 
 24 S = 0
 25 D = 0
 26 
 27 best_path = []
 28 best_path_index = 0
 29 
 30 res_fit = []
 31 
 32 # 路径
 33 paths = []
 34 # 最优路径
 35 # 迭代次数
 36 ITERATION_COUNT = 100
 37 #
 38 direction_arr = [(-1, -1), (0, -1), (1, -1), (-1, 0), (1, 0), (-1, 1), (0, 1), (1, 1)]
 39 
 40 
 41 def is_valid(point):
 42     if point[0] < 0 or point[1] < 0 or point[0] >= WIDTH or point[1] >= HEIGHT:
 43         return False
 44     return True
 45 
 46 
 47 # 计算欧式距离
 48 def distance(p1, p2):
 49     return math.sqrt((p1[0] - p2[0]) ** 2 + (p1[1] - p2[1]) ** 2)
 50 
 51 
 52 # 标号转坐标
 53 def mark2position(mark):
 54     return (mark % WIDTH, int(mark / WIDTH))
 55 
 56 
 57 def position2mark(position):
 58     return position[1] * WIDTH + position[0]
 59 
 60 
 61 # 5 6 7
 62 # 3   4
 63 # 0 1 2
 64 def generate_one_path(start, end):
 65     res = []
 66     res.append(start)
 67 
 68     s = start
 69     target_point = mark2position(end)
 70     dis = distance(mark2position(start), target_point)
 71 
 72     while (s != end):
 73         pos = mark2position(s)
 74         r = random.randint(0, 7)
 75         pos = (pos[0] + direction_arr[r][0], pos[1] + direction_arr[r][1])
 76         temp_dis = distance(pos, target_point)
 77         if is_valid(pos) and temp_dis <= dis:
 78             s = position2mark(pos)
 79             dis = temp_dis
 80             res.append(s)
 81     return res
 82 
 83 
 84 # 初代
 85 def init(count):
 86     res = []
 87     for i in range(0, count):
 88         res.append(generate_one_path(S, D))
 89     return res
 90 
 91 
 92 # 计算一条路径的适应度值
 93 def one_path_fit_val(path):
 94     sm = 0
 95     for i in range(1, len(path)):
 96         w = int(math.fabs(path[i - 1] - path[i]))
 97         if w == 1 or w == WIDTH:
 98             sm += DIS_2
 99         else:
100             sm += DIS_1
101     return MAX / sm
102 
103 
104 # 计算适应度值
105 def fitness():
106     res = []
107     max_fit = -1
108     global best_path
109     global best_path_index
110 
111     temp_best_path = []
112 
113     for i in range(len(paths)):
114         f = one_path_fit_val(paths[i])
115         res.append(f)
116         if f > max_fit:
117             max_fit = f
118             temp_best_path = paths[i]
119             best_path_index = i
120     best_path = copy.deepcopy(temp_best_path)
121     res_fit.append(max_fit)
122     return res
123 
124 
125 # 累计概率
126 def cumulative_probability(fits):
127     res = []
128     sm = sum(fits)
129     temp = fits[0] / sm
130     res.append(temp)
131     for i in range(1, len(fits)):
132         res.append(res[i - 1] + fits[i] / sm)
133     return res
134 
135 
136 # 选择 产生下一代
137 def choose(pArr, count):
138     res = []
139     for i in range(count):
140         p = random.random()
141         for j in range(len(pArr)):
142             if p <= pArr[j]:
143                 res.append(paths[j])
144                 break
145     return res
146 
147 
148 def cross_one_times(path1, path2):
149     # 求交集
150     temp = list(set(path1[1:-1]).intersection(set(path2[1:-1])))
151     sz = len(temp)
152     if sz == 0:
153         return (path1, path2)
154     r = random.random()
155     if r > cross_p:
156         index = random.randint(0, sz - 1)
157         e = temp[index]
158         t1 = path1.index(e)
159         t2 = path2.index(e)
160         p1 = path1[:t1]
161         p2 = path2[t2:]
162         p3 = path2[:t2]
163         p4 = path1[t1:]
164         p1.extend(p2)
165         p3.extend(p4)
166         return (p1, p3)
167     else:
168         return (path1, path2)
169 
170 
171 def cross():
172     n = len(paths)
173     res = []
174     for i in range(1, n, 2):
175         p = cross_one_times(paths[i], paths[i - 1])
176         res.extend(p)
177 
178     # 奇数情况
179     if len(res) < n:
180         res.append(paths[n - 1])
181     return res
182 
183 
184 # 判断三点之间是否联通
185 def is_valid_3_mark(m1, m2, m3):
186     # 重复
187     if m1 == m2 or m1 == m3 or m2 == m3:
188         return False
189     if m2 < MIN or m2 > MAX:
190         return False
191     # 不联通
192     if not (m1 + 1 == m2 or m1 - 1 == m2 or m1 + WIDTH == m2 or m1 - WIDTH == m2
193             or m1 + WIDTH + 1 == m2 or m1 + WIDTH - 1 == m2
194             or m1 - WIDTH + 1 == m2 or m1 - WIDTH - 1 == m2):
195         return False
196     # 不联通
197     if not (m3 + 1 == m2 or m3 - 1 == m2 or m3 + WIDTH == m2 or m3 - WIDTH == m2
198             or m3 + WIDTH + 1 == m2 or m3 + WIDTH - 1 == m2
199             or m3 - WIDTH + 1 == m2 or m3 - WIDTH - 1 == m2):
200         return False
201     return True
202 
203 
204 def variation_one_times(path):
205     r = random.random()
206     if r < variation_p:
207         return path
208     else:
209         sz = len(path)
210         if sz <= 2:
211             return path
212         # 变异点
213         prob_mark = []
214         var_index = random.randint(1, sz - 2)
215         pre_mark = path[var_index - 1]
216         cnt_mark = path[var_index]
217         next_mark = path[var_index + 1]
218         # 8中情况
219         temp_mark = [cnt_mark + 1, cnt_mark - 1, cnt_mark + WIDTH, cnt_mark - WIDTH, cnt_mark + WIDTH + 1,
220                      cnt_mark + WIDTH - 1, cnt_mark - WIDTH - 1, cnt_mark - WIDTH + 1]
221         for e in temp_mark:
222             if is_valid_3_mark(pre_mark, e, next_mark):
223                 prob_mark.append(e)
224 
225         if len(prob_mark) == 0:
226             return path
227         changed_mark = prob_mark[random.randint(0, len(prob_mark) - 1)]
228         path[var_index] = changed_mark
229         return path
230 
231 
232 def variation():
233     res = paths
234     for i in range(variation_times):
235         temp = []
236         for e in res:
237             temp.append(variation_one_times(e))
238         res = temp
239     return res
240 
241 
242 def output(g, f):
243     print("第" + str(g) + "代：最优路径：", end="", file=f)
244     print(best_path, end="", file=f)
245     print("适应度: ", end="", file=f)
246     print(fits[best_path_index], file=f)
247     for i, path in enumerate(paths):
248         print(str(i + 1) + ". ", end="", file=f)
249         print(path, end="", file=f)
250         print("适应度值：" + str(fits[i]), file=f)
251 
252 
253 def mark_screen_position(mark, x_min, y_max):
254     temp_p = mark2position(mark)
255     x = temp_p[0] - x_min
256     y = y_max - temp_p[1]
257     return (x, y)
258 
259 
260 def show(path, title):
261     canvas_width = 1000
262     point_r = 2
263     show_mark_min_width = 10
264     temp = []
265     for p in path:
266         temp.append(p % 100)
267     x_min = min(temp)
268     x_max = max(temp)
269     temp.clear()
270     for p in path:
271         temp.append(int(p / 100))
272     y_min = min(temp)
273     y_max = max(temp)
274     d = max(x_max - x_min + 1, y_max - y_min + 1)
275     grid_width = int(canvas_width / d)
276     canvas_width = grid_width * d
277     win = Tk()
278     win.title(title)
279     win.geometry(str(canvas_width) + "x" + str(canvas_width) + "+100+100")
280     can = Canvas(win, width=canvas_width, height=canvas_width, bg="white")
281     for i in range(0, canvas_width, grid_width):
282         can.create_line((0, i), (canvas_width, i))
283 
284     for i in range(0, canvas_width, grid_width):
285         can.create_line((i, 0), (i, canvas_width))
286     ft = tkFont.Font(root=win, family='Fixdsys', size=int(20 / 4), weight=tkFont.BOLD)
287     if grid_width >= show_mark_min_
288         for x in range(0, d):
289             for y in range(0, d):
290                 s = position2mark((x + x_min, y_max - y))
291                 can.create_text(x * grid_width + grid_width / 2, y * grid_width + grid_width / 2, text=s,
292                                 font=ft)
293     sz = len(path)
294     for i in range(0, sz - 1):
295         p1 = mark_screen_position(path[i], x_min, y_max)
296         p2 = mark_screen_position(path[i + 1], x_min, y_max)
297         can.create_line((p1[0] * grid_width + grid_width / 2, p1[1] * grid_width + grid_width / 2),
298                         (p2[0] * grid_width + grid_width / 2, p2[1] * grid_width + grid_width / 2), fill="red", width=3)
299         if i == 0: {
300             can.create_oval(
301                 (p1[0] * grid_width + grid_width / 2 - point_r, p1[1] * grid_width + grid_width / 2 - point_r,
302                  p1[0] * grid_width + grid_width / 2 + point_r, p1[1] * grid_width + grid_width / 2 + point_r),
303                 fill="blue")
304         }
305         can.create_oval((p2[0] * grid_width + grid_width / 2 - point_r, p2[1] * grid_width + grid_width / 2 - point_r,
306                          p2[0] * grid_width + grid_width / 2 + point_r, p2[1] * grid_width + grid_width / 2 + point_r),
307                         fill="blue")
308     can.pack()
309     win.mainloop()
310 
311 
312 # run point
313 random.seed()
314 S = random.randint(MIN, MAX)
315 D = random.randint(MIN, MAX)
316 while (S == D):
317     D = random.randint(MIN, MAX)
318 g = 1
319 fp = open("1.txt", "w", encoding="utf-8")
320 
321 # 初代
322 paths = init(PATH_COUNT)
323 fits = fitness()  # 适应度计算
324 output(g, fp)
325 g = g + 1
326 
327 origin_best_path = []
328 
329 for i in range(ITERATION_COUNT):
330     pArr = cumulative_probability(fits)  # 累计概率
331     paths = choose(pArr, PATH_COUNT - 1)  # 选择
332     paths = cross()  # 交叉
333     paths = variation()  # 变异
334     paths.append(best_path)
335     if i == 0:
336         origin_best_path = copy.deepcopy(best_path)
337     fits = fitness()  # 适应度计算
338     output(g, fp)
339     g = g + 1
340 fp.flush()
341 fp.close()
342 
343 fp = open("2.txt", "w", encoding="utf-8")
344 fp.write("最大适应度值列表：
")
345 for e in res_fit:
346     fp.write(format(e, ".2f"))
347     fp.write(" ")
348 fp.flush()
349 fp.close()
350 
351 t1 = threading.Thread(target=show, args=(origin_best_path, "初代最好的路径"))
352 t2 = threading.Thread(target=show, args=(best_path, "最好的路径"))
353 t1.start()
354 t2.start()
355 t1.join()
356 t2.join()

    效果图

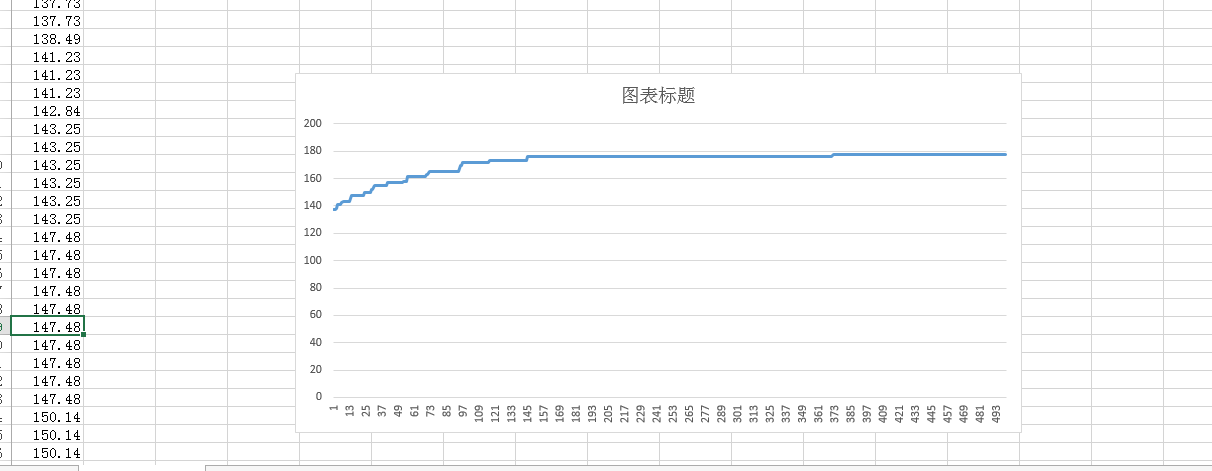
    图形显示
  • 相关阅读:
    STM32 GPIO 配置之ODR, BSRR, BRR 详解
    Understanding the STM32F0's GPIO
    STM32F4 External interrupts
    Calculate CAN bit timing parameters -- STM32
    禁用SQL Server Management Studio的IntelliSense
    SQL Server 2016中In-Memory OLTP继CTP3之后的新改进
    一张图解释SQL Server集群、镜像、复制、日志传送
    SQL Server出现错误: 4014
    SQL Server 2016五大优势挖掘企业用户数据价值
    SQL Server 2008, 2008 R2, 2012 and 2014 完全支持TLS1.2加密传输
  • 原文地址：https://www.cnblogs.com/oldBook/p/9900341.html
Copyright © 2020-2023  润新知