面向对象JML系列作业总结
一、综述
本单元作业,由简到难地迭代式实现了三种JML需求,主要学习了面向规格的编程方法。
- 第一次:实现Path类和PathContainer类
- 第二次:继承PathContainer类实现Graph类
- 第三次;继承Graph类实现RailwaySystem类
前两次作业的难度较低,最后一次作业在算法构造方面有难度,但总体来说,这三次作业在考察读懂规格,实现规格的功能方面难度较低。
二、JML语言理论基础、应用工具链
(一) JML语法总结
参考https://blog.csdn.net/piaopu0120/article/details/89527175这篇博客
方法规格语句
- 前置条件 requires P
- 后置条件 ensures P
- 副作用 assignable or modifiable
JML表达式
-
原子表达式 esult old(expr) ot_assigned(x,y,…) ot_modified(x,y,…) onnullelements(container) ype(type) ypeof(expr)
-
量化表达式 forall exists sum product max min um_of
-
集合表达式 new ST {T x|R(x)&&P(x)}
-
操作符 E1<:E2 b_expr1<>b_expr2 b_expr1<=!=>b_expr2 b_expr1>b_expr2 b_expr1<==b_expr2 othing everthing
其他语句
/*@ pure @ */
public normal_behavior / public exception_behavior
signals (***Exception e) b_expr / signals_only (***Exception e)
(二) openJML工具链使用
openJML主要是三个工具 具体参考https://course.buaaoo.top/assignment/66/discussion/198
-
语法检查:可以检查某个源文件中的JML语法是否合法
openjml -check <source files> -
静态检查
openjml -esc <source files> -
运行时检查
openjml -rac <source fils>
三、JMLUnitNG/JMLUnit
琢磨了很久,并没有成功把自己的MyGraph类搞定。不过还是可以跑一些比较小的Demo的,我参考讨论区大佬的帖子跑了一个Demo。
- 生成测试文件

- 用 javac 编译 JMLUnitNG 生成文件
- 用 jmlc 编译自己的文件

- 测试
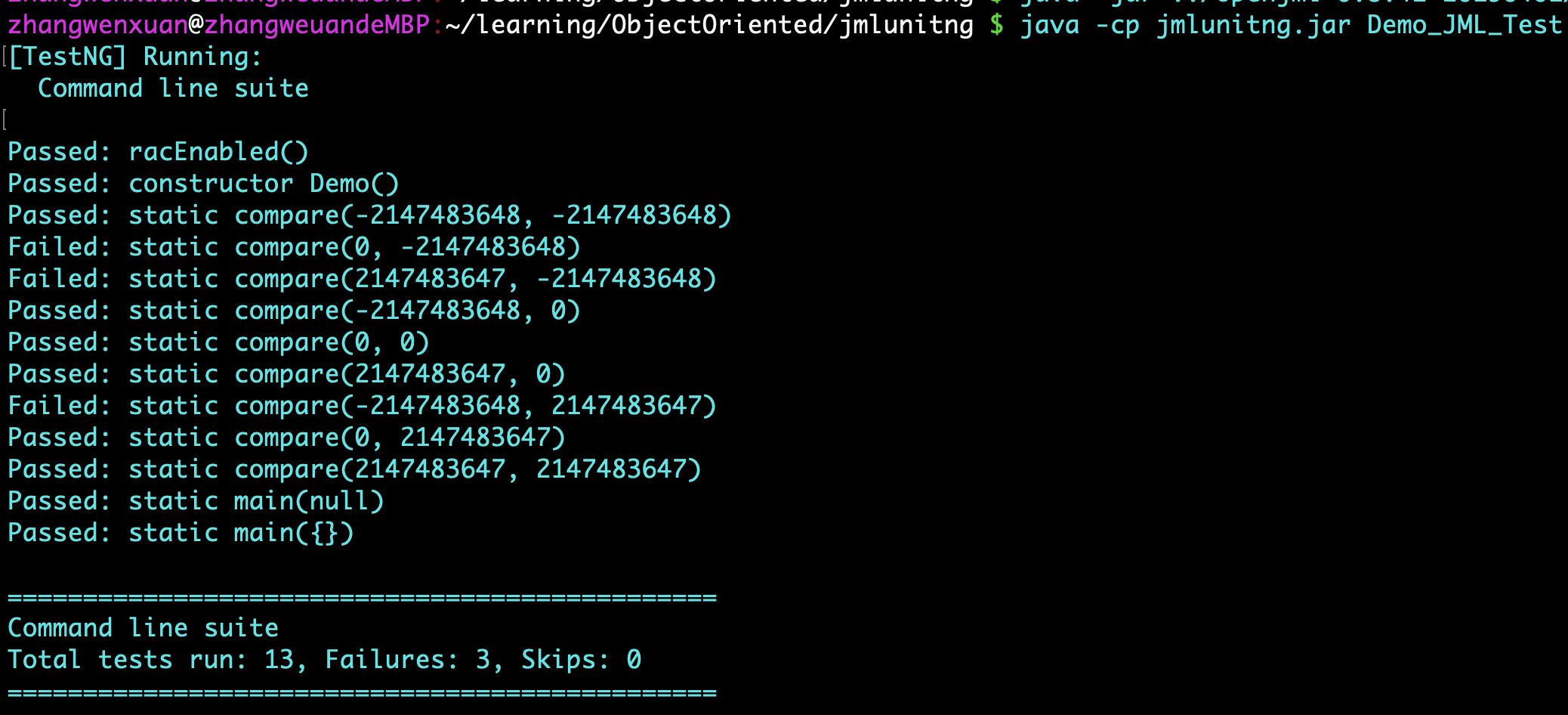
四、分析程序架构
第一次作业
第一次作业要求实现已经定义好规格的Path类和PathContainer类,为了尽可能降低时间复杂度,我一共采用了五个容器来实现这两个类的功能。
Path类需要满足顺序存储,还有快速查询。所以定义一个ArrayList来实现顺序存储,定义一个Set来实现快速查询。PathContainer类需要满足path与pathid直接的相互转化,通过Map实现path到id的转换,通过数组实现id到path的转换,同时还有一个需求是数容器中所有的不同节点个数,我通过一个Map记录每个节点的总出现次数,在addPath和rmPath的过程中更新这个Map,这个Map的size能满足这个需求。
第二次作业
第二次作业在第一次PathContainer的基础上实现Graph类,需要实现的主要功能是求两节点之间的最短距离,每个边的边权为1。因为边权相同,我通过bfs的方式来遍历每个节点,最先搜到的节点就是这两个节点间最短的距离。
定义一个邻接表类,用ArrayList<HashSet<>>存储邻接表,用二维数组存储距离矩阵,同时有一个问题需要解决,nodeid的数据范围在整个int,距离矩阵的索引不可能是整个int的,因此需要使用hashmap将int范围的nodeid映射到小范围正整数的id,由此便可以实现邻接表的构建,再由bfs求出距离了。
第三次作业
第三次作业在第二次Graph的基础上实现RailwaySystem类,需要多实现4个功能,求连通块个数,求两点间最少换乘数,求两点间最少票价,求两点间最小不满意度。
这次作业的难点在于算法和数据结构设计,使得满足时间复杂度。
-
首先连通块个数,可以在第二次作业的bfs中通过加入染色法直接顺便求出来。
-
最少换乘数的求法比较多,我采取的方法如下,构建一个新的图PathMap,将每一条Path看作一个节点,节点间有边当且仅当两个Path间有公共节点。通过这种方式,两点间的最短换乘数,转换为其所在Path在PathMap中的最短距离。
-
最少票价和最小不满意度,我采取拆点方式实现,通过添加结点和边,使换乘的代价也整合到图中。拆点算法是控制复杂度的关键,若采取等价节点之间用完全图来连接,将多产生(n^2)级的边数,因此我采用菊花图式的拆点方式,用菊花点连接到每个等价节点,形成星型拓扑结构,每条边的边权为换乘代价的一半,这样保证了每两点之间的联通且权值满足要求。
在实现时有以下trick
- 最小不满意度可以使用dijkstra求,最少票价可以直接使用bfs,因为加入菊花点后,边权都是1了。
- 每个相同站点都实现一个菊花点,尽管这个站点只在一条线路上有。这样更统一,方便查询。
- 查询的时候,只需要从from菊花点搜到to菊花点,得到的距离减掉一个换乘代价即为所求距离。
- 距离矩阵只需要存菊花点到菊花点的就行了,最多120*120。否则需要4000*4000量级。
- 采用缓存机制,不需要一次性把所有节点的dijksta和bfs都求出来,问哪个求哪个,求完存起来,图结构改变时全删掉。
五、测试
本单元学习了使用junit单元测试,通过单元测试,可以对实现的每一个方法进行测试,junit还能分析分支覆盖率,帮助我们覆盖全部分支,使得测试更充分。
麻烦的地方是,采用junit需要编写大量代码,而且测试数据也需要自己编写,对于完全由自己实现的代码来说,采用junit框架显得有些冗余,不过对于多人合作的项目来说,junit的框架是十分有效的。
六、面向规格的程序设计
这一单元,我们学习了面向规格的程序设计,规格是一种规范,凡是满足规格要求的实现都是正确的,规格为实现者提供规范,为测试者提供说明,是一种规范严谨且高效的程序开发模式。
在我们今后的学习中,很可能不会再写规格或者读规格,但是这种规格化编程的思想将会一直指导我们如何进行设计架构,如何将需求更加严谨地解释出来,我觉得这正是oo课程这一单元的意义所在。