Morris Traversal

昨天临近要睡觉的时候做了一个leetcode题目，“Recover BST”,算法很容易就想到了，直接找出两个异常点就好了，但是我写的算法是用栈实现的非递归遍历，空间复杂度是O(N),虽然比递归的要好点，但是题目说明里面那句“如果能用constant space ”却让我百思不得其解。难道我的解法不是最精简的？

我的解法说白了就是个preorder traversal，难道有可以不用traversal的办法，结果在discuss里面发现了一块代码，但是没怎么看明白了，接下来搜索资料，才知道这种解法叫“Morris Traversal”，实际上就是一种O(1)空间复杂度，O(N)空间复杂度的遍历方法。

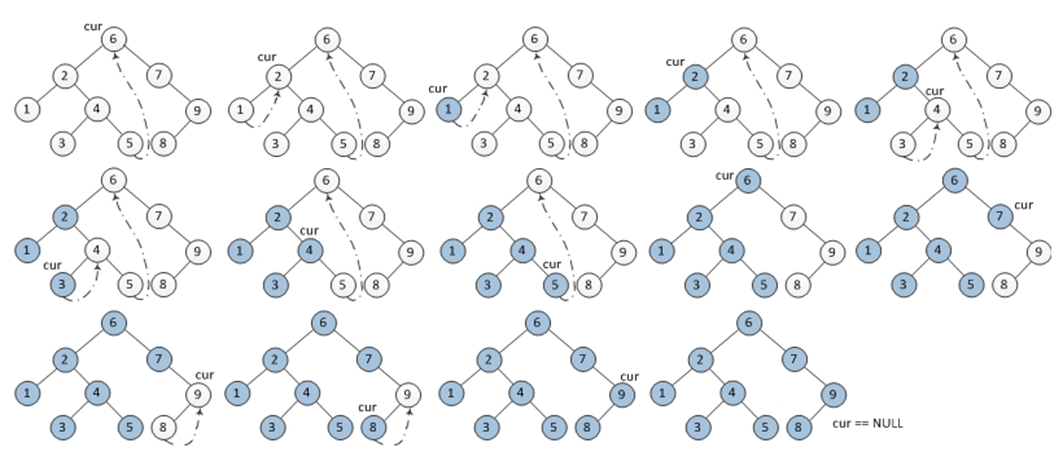
我们知道，在深度搜索遍历的过程中，之所以要用递归或者是用非递归的栈方式，都是因为其他的方式没法记录当前节点的parent,而如果在每个节点的结构里面加个parent 分量显然是不现实的，那么Morris是怎么解决这一问题的呢？好吧，他用得很巧妙，实际上是用叶子节点的空指针来记录当前节点的位置，然后一旦遍历到了叶子节点，发现叶子节点的右指针指向的是当前节点，那么就认为以当前节点的左子树已经遍历完成。

以inorder为例，初始化当前节点为root，它的遍历规则如下：

• 如果当前节点为空，程序退出。
• 如果当前节点非空，
  • 如果当前节点的左儿子为空，那么输出当前节点，当前节点重置为当前节点的右儿子。
  • 如果当前节点的左儿子非空，找到当前节点左子树的最右叶子节点（此时最右节点的右儿子有两种情况，一种是指向当前节点，一种是为空,你也许感到奇怪，右节点的右儿子怎么可能非空，注意，这里的最右叶子节点只带的是原树中的最右叶子节点。），若其最右叶子节点为空，令其指向当前节点，将当前节点重置为其左儿子，若其最右节点指向当前节点，输出当前节点，将当前节点重置为当前节点的右儿子,并恢复树结构，即将最右节点的右节点再次设置为NULL

代码如下：

void MorrisTraversal(TreeNode * root)
{
    TreeNode *cur = root;
    TreeNode *rightmost;
    while(cur)
    {
        if(cur->left)
        {
            rightmost = cur->left;
            while(!rightmost->right&&rightmost->right！=cur)
            {
                rightmost=rightmost->right;
            }

            if(!rightmost->right)rightmost->right = cur;
            else {cout<<cur->val<<" ";cur = cur->right;rightmost->right=NULL;}
        }

        else {cout<<cur->val<<" ";cur = cur->right;}
    }
}

需要注意的是，世界上没有白吃的午餐，虽然这个遍历的时间复杂度还是O(N)，但是此O(N)比之于用了栈的O(N)前面的系数还是要大些的，多出的耗费主要集中在寻找最右叶子。

对于preorder的情况，稍微将inorder的情况改写一下就好了。详情参考这篇文章。有人画了一幅图，其实这幅图看了作用也不大，只需要知道的是，本解法的关键在于，用当前节点的左子树的最右也自己点的右指针指向当前节点，使得恢复路径成为了可能。