一、基本概念
1、连通图:任意两个结点都连通(不需要直接相连,只要有路径即可)
强连通图:有向图中的概念,任意两个结点都有双向路径,比如a->b 和 b->a 都有路径(不要求直接相连,只要有路径即可)
如果有一条u到v的有向路径,同时有一条v到u的有向路径,则称为两个顶点的强连通。
顶点数目大于1的强连通分量中必然存在回路。
2、n个顶点的连通图(或者强连通图)最少有多少条边?
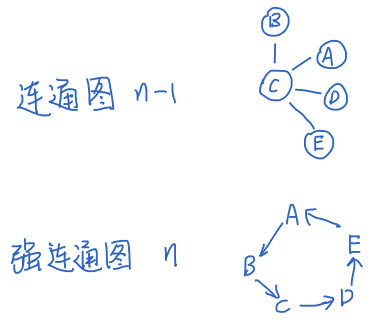
3、极大连通子图:
极大是因为加入任何一个不在图中的点集都会导致不再连通。
连通图只有唯一极大连通子图,就是本身。
非连通图,有多个极大连通子图。(非连通图的极大连通子图叫做连通分量,每个分量都是一个连通图)
————————————————————————————————————————————————
下图为非连通图,图中有两个极大连通子图(连通分量)。
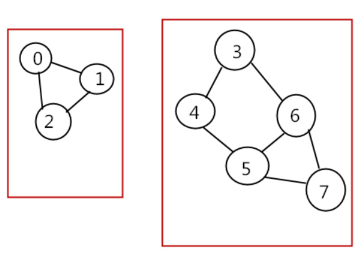
4、极小连通子图:只能存在于连通图中
极小是因为连通子图包含的边最小,删除任何一条边,就无法构成树。
———————————————————————————————————————
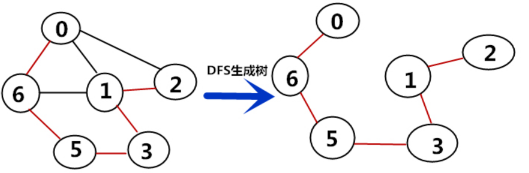
5、连通分量:无向图中的概念, 指的是连通图的极大连通子图。
连通图的连通分量只有1个,就是本身。非连通图(必须是无向图)有多个连通分量。
子图一定包含所有顶点,边可以为空,但是顶点不行。顶点也是一种图。
强连通分量:有向图中的概念,首先这个图是强连通的,就是任意两个结点都有双向路径相连。这样的一个图的极大强连通子图,称为强连通分量。
单独的一个顶点,也构成一个强连通分量。
6、生成树:包含全部顶点的极小连通子图,n个顶点的图生成树有n-1条边(见4中的示意图)
生成森林:非连通图中所有连通分量(也就是极大连通子图)的生成树,组成森林(见3中的示意图)。
7、顶点的度:以该顶点为一个端点的边的数目。
对于有n个顶点,e条边的图来说。
无向图中:度的总数为2e ,因为每一个边有2个端点,生成2个度,所以总共有2e个度。
有向图中:一条边可以产生一个入度,一个出度,所以入度的个数=出度的个数=2,总度数=入度+出度=2e。
8、网:就是在图中给每条边增加一个权重。
稀疏和稠密的界定:|E|<|V|*log|V| , E指边数,V指结点数。
9、路径:从顶点 v 到 w 所经过的顶点的序列。
简单路径:路径中的顶点不重复。
距离:最短的路径长度
回路:第一个顶点和最后一个顶点相同的路径。
10、完全图:就是图中任何两个结点,都有路径直接相连。
无向完全图:任意两个结点直接相连,不带方向。
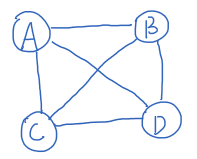
有向完全图:符合完全图的定义,并且任意两个结点之间都有方向相反的两条线连接。
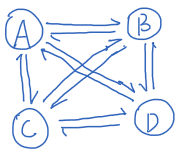
二、图的存储及基本操作
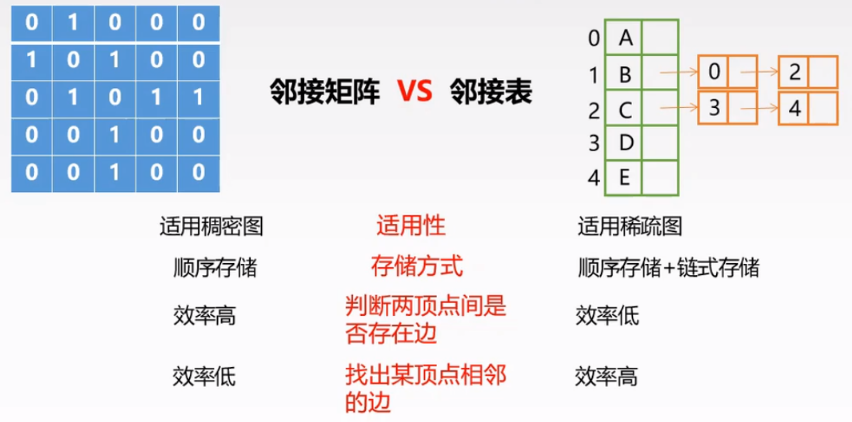
1、邻接矩阵和邻接表法:
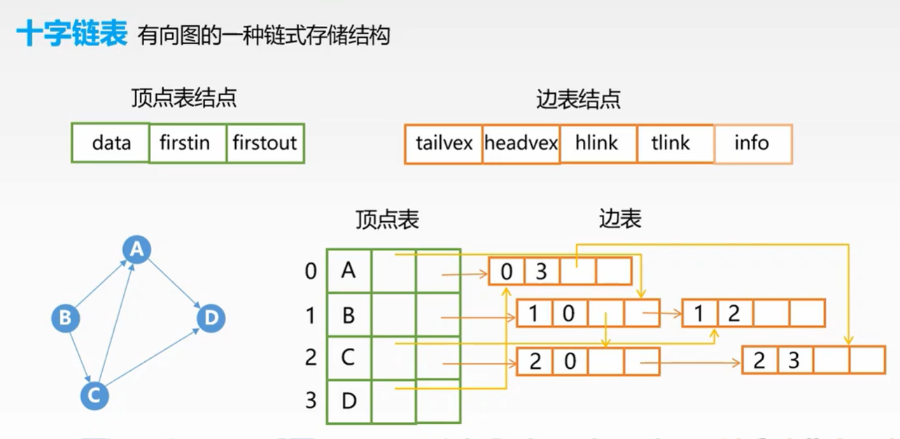
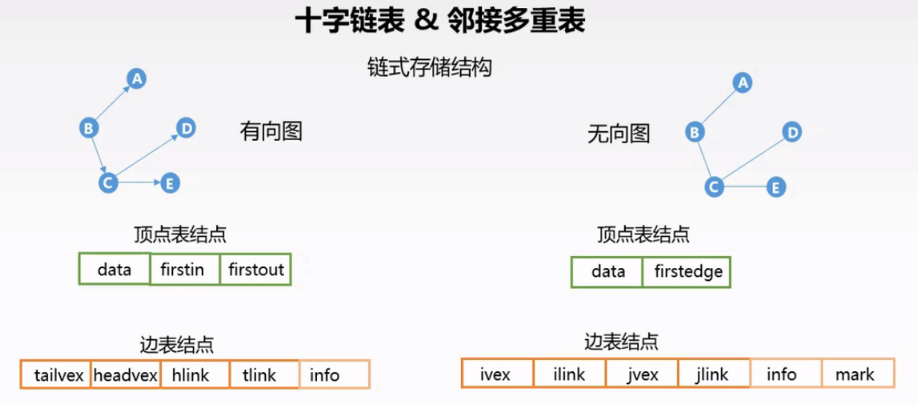
2、十字链表:用在有向图上,解决了有向图中无法快速找到某顶点入边的这一弊端。
出度和邻接表一样,入度指向出度的边表。
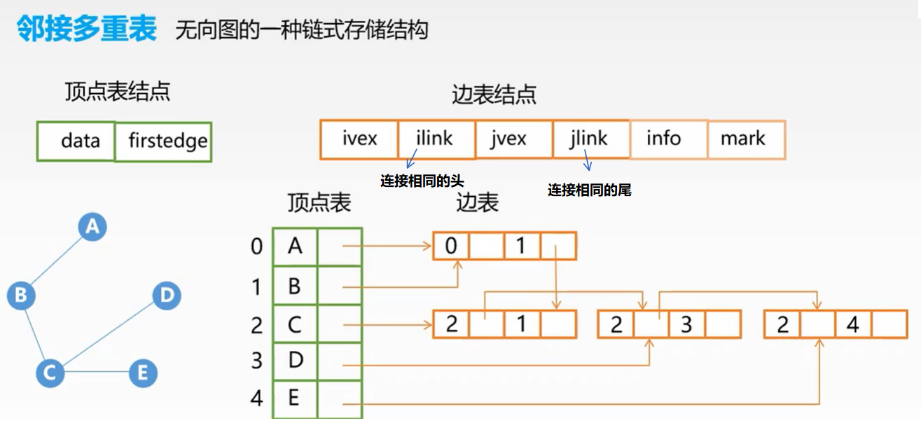
3、邻接多重表:用在无向图上,解决无向图中每一个结点都需要两个边表结点存放的弊端。
4、任意一个顶点的度:
邻接矩阵无向图:顶点 i 的度等于第 i 行中 1 的个数。
邻接矩阵有向图:出度等于第 i 行中1的个数,入度等于第 i 列中1的个数。
邻接表无向图:顶点 i 的度数等于顶点表结点 i 的右边对应的边表结点的个数。
邻接表有向图:出度等于顶点表结点 i 的右边对应的边表结点的个数, 顶点 i 的入度等于邻接表中所有编号为 i 的边表结点数。度数=入度+出度。