树的性质:
1、高度为 m 的树中第 i 层上至多有 mi-1 个结点(i≥1)。
2、高度为 h 的 m 叉树至多有(mh-1)/(m-1)个结点。
证明:等比数列求和 S=1+m+m2+......mh-2+mh-1=(mh-1)/(m-1) , 注意等比数列求和的n指的是相数而不是最高项的次数。
3、具有n个结点的m叉树的最小高度为⌈logm(n(m-1)+1)⌉。
证明:思路是只有当这n个结点建立的m叉树为满的时候,树的高度才会最低。
层次 度为3时的结点数 度为m时的结点数
1 3^0 m^0
2 3^1 m^1
3 3^2 m^2
………………………………………………
i 3^(i-1) m^(i-1)
………………………………………………
h 3^(h-1) m^(h-1)
所以得到n=m^0+m^1+…+m^(h-1)=(m^h-1)/(m-1),解得h>=logm(n(m-1)+1),即logm(n(m-1)+1)向上取整。
4、树的路径长度是指树根到每个结点的路径长的总和,根到每个结点的路径长度的最大值应是树的高度减1。(注意与哈夫曼树的带权路径长度区别)
5、常见的树结点与度之间的关系:
a. 总结点数=n0+n1+n2+....+nm
b. 总分支数=1n1+2n2+....+mnm(度为m的结点引出m条分支)
c. 总结点数=总分支数+1
二叉树的性质:
1、在含有n个结点的二叉链表中,含有n+1个空链域(重要结论)。
证明:首先要明白链域是什么意思:
a. 链就代表指针,就是下个元素的地址。
b. 链表中一个结点可以分为两个部分,也可以说是区域,一个区域存放指针,被称为指针域,另一个区域存放数据,叫做数据域。链表中的指针域中的内容就是指针,单链表中一个指针域存放一个指针,双链表中两个指针域各存放一个指针。


2、若 i≤⌊n/2⌋ ,则结点 i 为分支结点,否则为叶子结点。
3、若 n 为奇数,则每个分支结点都有左孩子和右孩子;若 n 为偶数,则编号最大的分支结点(编号为n/2)只有左孩子,没有右孩子,其余分支结点左、右孩子都有(默认是指完全二叉树,包括满二叉树)。
证明:性质2和3本质上是同一件事,即:
如何证明对于编号为 i 的结点,若有双亲,则其双亲为 ⌊i/2⌋,若有左孩子,则左孩子为2i;若有右孩子,则右孩子为2i+1。
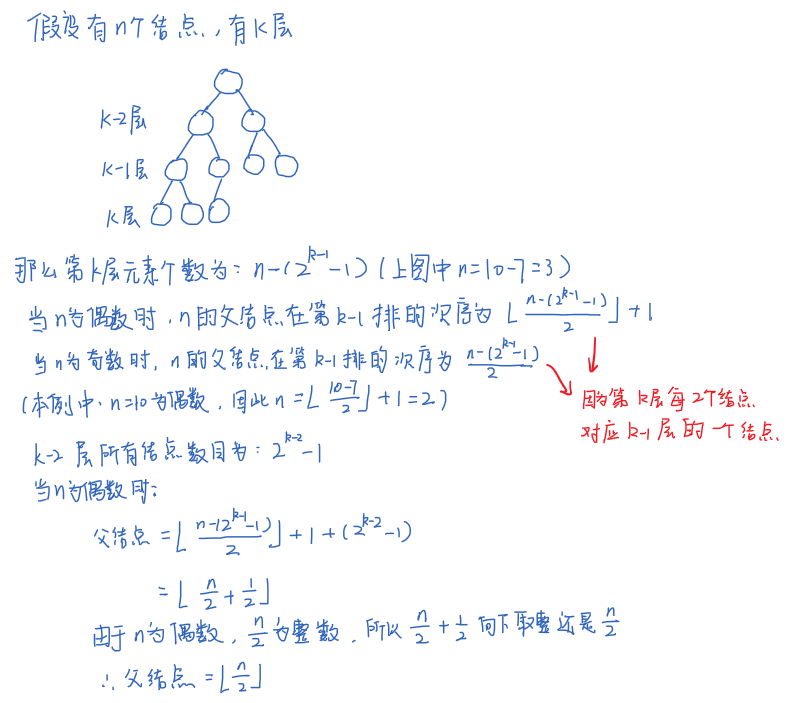

推广到满 m 叉树:
规定:高度h,满m叉树,根结点在第1层,顺序编号。

4、具有n个(n>0)结点的完全二叉树的高度为 ⌈log2(n+1)⌉ 或 ⌊log2n⌋ +1 。
证明:

5、分支结点:就是总结点减去叶子结点。
6、二叉树的宽度:具有最多结点数的层中包含的结点数。
森林的性质:
1、对森林所对应的二叉树进行中序遍历,相当于对森林中的每一棵树从左到右进行后序遍历。